Download Digital Intro

Announcements
• Assignment 5 due tomorrow (or now)
• Project ideas due Nov 1st. (email 1
paragraph, plus web links)
• No new assignment this week. Revise!
• Mid-term next Thursday (27th)
– Go through the Lectures, Assignments and
Solutions
– Use EWB to create test problems
– Google “circuit analysis problems”!
Lecture 14
•
•
•
•
•
Real world op amps
Op amp Slew Rate
Introduction to digital signals
Number codes
Digitization
Non-Ideal Opamps: Basic Cautions
1) Avoid Saturation
• Voltage limits: VS-< vOUT < VS+
• In the saturation state, Golden
Rules of opamp are not valid
Basic Cautions for opamp circuits
2) Feedback must be negative (inverting) for linear behaviour
3) There must always be negative feedback at DC (i.e. when ω=0).
• Otherwise any small DC offset will send the opamp into saturation
• Recall the integrator: In practice, a high-resistance resistor should be added in parallel
with the capacitor to ensure feedback under DC, when the capacitive impedance is high
4) Don't exceed the maximum differential voltage limit on the inputs: this can
destroy the opamp
Frequency response limits
• An ideal opamp has open-loop (no feedback) gain A=
• More realistically, it is typically ~105-106 at DC, dropping to 1 at
frequency, fT=1-10 MHz
• The opamp also introduces a phase shift between input and output
• At high frequencies, as the open-loop gain approaches 1, the phase
shift increases
• If it reaches >180º degrees, and the open loop gain is >1, this results
in positive feedback and high frequency oscillations
• The term "phase margin" refers to the difference between the phase
shift at the frequency where the gain=1 (fT) and 180º
Frequency response limits
• Open loop cut-off frequency, f0 (also known as open loop bandwidth)
is usually small (typically 100Hz) to ensure that the gain is <1 at a
phase shift of 180º
• Closed-loop gain (gain of amplifier with feedback) begins dropping
when open loop gain approaches RF/RS (in the case of the inverting
amp)
• Cut off frequency will be higher for lower closed-loop gain circuits
Inverting amplifier
Slew rate (or rise time)
• The maximum rate of change of the output of an opamp is known as
the slew rate (in units of V/s)
dvo
S0 
dt
max
square wave input
• The slew rate affects all signals - not just square waves
• For example, at high enough frequencies, a sine wave input is
converted to a triangular wave output due to limited slew rate
Slew rate example
• Consider an inverting amplifier, gain=10, built using an opamp with a
slew rate of S0=1V/μs.
• Input a sinusoid with an amplitude of Vi=1V and a frequency, ω.
vi  Vi cos(t )  vo   AVi cos(t )
dvo
dv0
 AVi sin( t ) 
dt
dt
dvo
dt
 AVi  S0
max
 10  106    105
max
• For a sinusoid, the slew rate limit is of the form AViω<S0.
• We can therefore avoid this non-linear behaviour by
• decreasing the frequency (ω)
• lowering the Amplifier gain (A)
• lower the input signal amplitude (Vi)
• Typical values: 741C: 0.5V/μs, LF356: 50V/ μs, LH0063C: 6000V/ μs,
Op Amp Slew rate (or rise time)
• The maximum rate of change of the output of an opamp is known as
the slew rate (in units of V/s)
dvo
S0 
dt
max
square wave input
• The slew rate affects all signals - not just square waves
• For example, at high enough frequencies, a sine wave input is
converted to a triangular wave output due to limited slew rate
Slew rate example
• Consider an inverting amplifier, gain A=10, built using an opamp with
a slew rate of S0=1V/μs.
• Input a sinusoid with an amplitude of Vi=1V and a frequency, ω.
vi  Vi cos(t )  vo   AVi cos(t )
dvo
dv0
 AVi sin( t ) 
dt
dt
dvo
dt
 AVi  S0
max
 10  106    105
max
• For a sinusoid, the slew rate limit is of the form AViω<S0.
• We can therefore avoid this non-linear behaviour by
• decreasing the frequency (ω)
• lowering the Amplifier gain (A)
• lower the input signal amplitude (Vi)
• Typical values: 741C: 0.5V/μs, LF356: 50V/ μs, LH0063C: 6000V/ μs,
Stop Revising Here
Stop Revising Here
Stop Revising Here
Digital Electronics
• Some simple concepts to begin with
• Question: Why do we use digital
electronics?
• Allows transmission of analog signals (data) without
degradation
• Allows easy storage of data
• Allows to perform calculations on the data
Why use digital circuits?
• Digital signals, represented by ones and zeros,
are very easy to handle with electronic circuits.
• Only 2 states are required, e.g:
–
–
–
–
Switch ON or OFF
Circuit CLOSED or OPEN
Current FLOWING or NOT
Voltage HIGH or LOW
• This leads to a low error rate - compare the
accurate measurement of voltage required in an
analog circuit to the requirement in digital, which
is typically 0V-2V=0, 2.6V-5V=1
How can digital help?
• Any numbers, letters and symbols can be
represented using multiple binary digits
• e.g. binary 101=5
• If we first digitize the analog signal, we
only need transmit a stream of 1's and 0's
Digital system
So, Ideally:
What happens now
when we add noise?
Digital system
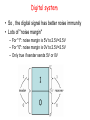
• So , the digital signal has better noise immunity
• Lots of "noise margin"
– For "1": noise margin is 5V to 2.5V=2.5V
– For "0": noise margin is 0V to 2.5V=2.5V
– Only true if sender sends 5V or 0V
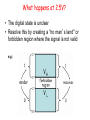
What happens at 2.5V?
• The digital state is unclear
• Resolve this by creating a "no man’s land" or
forbidden region where the signal is not valid
e.g:
Helps a bit… but we can do better.
If the sender sends a high state (1) = VOH
or a low state (0) =VOL
Little or no
noise on the
output voltage
from sender
Input voltage to
receiver must
allow for
possible noise
contamination
It makes sense to have different thresholds for input and output voltage levels:
High state ("1") noise margin is: VIH-VOH
Low state ("0") noise margin is: VIL-VOL
What is the noise margin?
So :
The input high threshold is lower than the output high threshold
The input low threshold is higher than the output low threshold
Digital systems follow a discipline:
If inputs to the system meet the valid input thresholds, the
system guarantees that its outputs will meet the valid output
thresholds
e.g. TTL output: LOW<0.4V, HIGH>2.4V
TTL input: LOW < 0.8V, HIGH > 2.0V
0.4V noise margin
How do we represent analog as digital?
Number codes: How to count!
Decimal counting: each column is a power of ten
Power of 10:
Weight:
3
1000
103
2
100
102
1
10
101
0
1
100
requires 10 symbols: 0,1,2,3,4,5,6,7,8 and 9
Example: 1998 = (1*103) + (9*102) + (9*101) + (8*100)
= 1000 + 900 + 90
+ 8
Binary Counting
Binary counting: each column is a power of two
Power of two: 7
Weight:
128
27
6
64
26
5
32
25
4
16
24
3
8
23
0
8
0
4
2
4
22
1
2
21
requires 2 symbols: 0 and 1
Example: Convert 1100010 to decimal
Binary: 0
1
1
0
Weight:128
64
32
16
64 + 32
= 98
1
2
+ 2
0
1
0
1
20
Definitions
• 1 binary digit is a "bit".
• 8 bits are a "byte” (B)
• 1kB = 210 B = 1024 B
• 1MB = 210 kB = 220 B = 1,048,576 B
• More than 8 bits are a "word" (no fixed size – depends on architecture:
Intel 8086 used 16 bit words, modern 32 or 64 bit processors keep this
definition)
• "Least significant bit" refers to the rightmost bit ( the 20 position)
• "Most significant bit" refers to the leftmost bit (e.g. the 27 position in a byte)
Algorithm to convert decimal to binary
Easy - divide by two and write down the remainder
e.g. decimal 23
23 divide by 2 = 11 remainder
11 divide by 2 = 5 remainder
5 divide by 2 = 2 remainder
2 divide by 2 = 1 remainder
1 divide by 2 = 0 remainder
so 23 decimal is binary 10111
Convert 15710 to binary
Answer:10011101
1
1
1
0
1
Addition of binary numbers
1+0=1
1 + 1 = 10
1 + 1 + 1 = 11
Don't forget to carry!
Which of the following is not true?
A: 10 + 10 = 110
B: 11 + 11 = 110
C: 101 + 1 = 110
Answer: A (=100)