Download Pythagorean Theorem

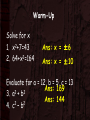
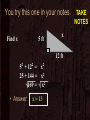
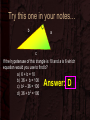
Pythagorean Theorem
MCC8.G.7: Apply the
Pythagorean Theorem to
determine unknown side lengths
in right triangles in real-world
and mathematical problems in
two and three dimensions.
Warm-Up
Solve for x
1. x2+7=43
2. 64+x2=164
Ans: x = ±6
Ans: x = ±10
Evaluate for a = 12, b = 5, c = 13
Ans: 169
2
2
3. a + b
Ans: 144
2
2
4. c – b
Essential ??
• How can we use the
Pythagorean Theorem to
solve for a missing length
of a right triangle?
Pythagorean Theorem
No need
For notes
On this slide
• What is the Pythagorean Theorem in
symbol form?
2
a
+
2
b
2
c
=
• Which of these variables represent the
hypotenuse?
c
• Once you have figured out which is c,
does it matter which leg is a and which
is b?
no
Steps to Solve for a missing side
TAKE
of a right triangle using the
NOTES
Pythagorean Theorem
Step 1: Write the formula
Step 2: Substitute known values for the
variables.
Step 3: Solve the equation for the missing
variable.
Example 1
Find x
8 ft
x
TAKE
NOTES
15 ft
• Step 1: Write the formula
a2 + b2 = c2
• Step 2: Substitute known values 82 + 152 = c2
Which number goes where?
You need to identify the hypotenuse. It’s the one opposite
of the right angle.
The hypotenuse is always going to be the c in the formula.
Since we do not know the value of c, it stays as c in the formula.
Does it matter whether we use a = 8 or 15? No.
Let’s use a = 8 and b = 15.
Example 1
Find x
TAKE
NOTES
x
8 ft
15 ft
• Step 1: Write the formula
a2 + b2 = c2
• Step 2: Substitute known values 82 + 152 = c2
• Step 3: Solve for the missing variable, in this case c.
We are not done yet…
We have found c2, but
not just plain c.
We were told to solve for x, not c.
So we should replace the c with an x.
64 + 225 = c2
289 = c2
289 = c2
17 = c
x = 17
You try this one in your notes.
Find x
5 ft
x
12 ft
52 + 122 = x2
25 + 144 = x2
169 = x2
• Answer:
x = 13
TAKE
NOTES
TAKE
NOTES
x
Example #2
Find x.
Round to the nearest
hundredth.
14 in
6 in
• Step 1: Write out the formula
• Step 2: Substitute known values
a2 + b2 = c2
a2 + 62 = 142
Which number goes where?
This time we are given the hypotenuse. So, c = 14
Does it matter whether we use a = 6 or b = 6?
Let’s use b = 6.
No
TAKE
NOTES
Example #2
Find x.
Round to the nearest
hundredth.
14 in
x
6 in
a2 + b2 = c2
a2 + 62 = 142
• Step 1: Write out the formula
• Step 2: Substitute known values
• Step 3: Solve for the missing variable, in this case a.
Can we just add the two numbers and do
the square root?
No, they are not on
the same side of the equals sign.
x = 12.65
a2 + 36 = 196
– 36 – 36
a2 = 160
a2 = 160
a = 12.64911
What is the difference between No need
For notes
On this slide
the 2 examples?
• Both have you squaring the given sides.
• Both have you using the square root at the
end.
• The only difference is in the middle.
– Example 1 has you adding the numbers
– Example 2 has you subtracting the smaller from
the larger.
What does this mean?
• When you have two sides of a right triangle,
you can find the third using the Pythagorean
Theorem.
• Square both of the measurements you have.
• Add or subtract the two numbers depending
on whether or not you have the hypotenuse.
(Subtract if you have it, add if you don’t)
• Find the square root of the result and you
have your missing side!
Try this one in your notes…
x
15
20
Solve for x.
Round your answer to the nearest hundredth if necessary.
Answer: 25
Try this one in your notes…
7
12
x
Solve for x.
Round your answer to the nearest hundredth if necessary.
Answer: 13.89
Try this one in your notes…
5
x
3
Solve for x.
Round your answer to the nearest hundredth if necessary.
Answer: 4
Try this one in your notes…
30
7
x
Solve for x.
Round your answer to the nearest hundredth if necessary.
Answer: 30.81
Try this one in your notes…
b
a
c
If the hypotenuse of this triangle is 10 and a is 6 which
equation would you use to find b?
a) 6 + b = 10
b) 36 + b = 100
c) b2 – 36 = 100
d) 36 + b2 = 100
Answer: D