Download - Sacramento - California State University

IDENTIFICATION OF FOOTHILL YELLOW-LEGGED FROG INDIVIDUALS
THROUGH AUTOMATED PATTERN RECOGNITION
A Project
Presented to the faculty of the Department of Electrical and Electronic Engineering
California State University, Sacramento
Submitted in partial satisfaction of
the requirements for the degree of
MASTER OF SCIENCE
In
Electrical and Electronic Engineering
by
Orion Kemp Leland
Neil Ernest Gee
SPRING
2014
© 2014
Orion Kemp Leland
Neil Ernest Gee
ALL RIGHTS RESERVED
ii
IDENTIFICATION OF FOOTHILL YELLOW-LEGGED FROG INDIVIDUALS
THROUGH AUTOMATED PATTERN RECOGNITION
A Project
by
Orion Kemp Leland
Neil Ernest Gee
Approved by:
__________________________________, Committee Chair
Dr. Fethi Belkhouche
__________________________________, Second Reader
Dr. Preetham Kumar
____________________________
Date
iii
Student: Orion Kemp Leland
Neil Ernest Gee
I certify that these students have met the requirements for format contained in the University
format manual, and that this project is suitable for shelving in the Library and credit is to be
awarded for the project.
__________________________, Graduate Coordinator ___________________
Dr. Preetham Kumar
Date
Department of Electrical and Electronic Engineering
iv
ABSTRACT
of
IDENTIFICATION OF FOOTHILL YELLOW-LEGGED FROG INDIVIDUALS
THROUGH AUTOMATED PATTERN RECOGNITION
by
Orion Kemp Leland
Neil Ernest Gee
Photographic identification of individuals using natural physical markings provides important
information for studying wildlife population demographics. The Foothill Yellow-legged Frog
(Rana boylii, FYLF) is a species with unique chin-spot patterns that researchers currently identify
through manual comparison of photographs in search of matching markings. However, these
commonly employed methods, which can involve manually comparing many hundreds of images,
are both time consuming and potentially inaccurate. In this project, we address this problem by
defining a process that automates the identification of FYLF individuals from images using
MATLAB-based image processing and pattern recognition techniques. We tested the process
using replica frogs with patterns based on actual FYLF chin-spot patterns. This method
effectively found matches in frogs when the individual spots had complex shapes. However, the
process less effectively recognized patterns that were based primarily on spot location. This
project provides several valuable tools researchers can use to identify FYLF individuals and can
be the foundation for a more optimal system.
v
_______________________, Committee Chair
Dr. Fethi Belkhouche
_______________________
Date
vi
ACKNOWLEDGEMENTS
Firstly, we would like to thank Ryan Peek at the Center for Watershed Sciences, University of
California, Davis for presenting us with an interesting problem and the many images of frogs
used to develop and test our process.
We would like to thank our adviser, Professor Fethi Belkhouche, for the support and careful
guidance through the development of our project. Thanks for your enthusiasm and willingness to
explore something a little different.
Thank you to Jim Ster, Mike Newton, and the ECS Tech Shop team for help with the design and
fabrication of the image-capturing box. You provide an invaluable service to all of the
engineering students.
Lastly, we would like to thank Alison Whipple for your support and spot-on advice, particularly
during the editing portion of the project, and Heather Baker for your encouragement and patience.
vii
TABLE OF CONTENTS
Page
Acknowledgements ........................................................................................................................ vii
List of Tables .................................................................................................................................. xi
List of Figures ................................................................................................................................ xii
Chapter
1. INTRODUCTION ..................................................................................................................... 1
Overview ........................................................................................................................ 1
Wildlife Pattern Matching .............................................................................................. 2
Project Overview ............................................................................................................ 3
2. BACKGROUND ....................................................................................................................... 6
Overview ........................................................................................................................ 6
Hausdorff Dimension ..................................................................................................... 6
Elliptic Fourier Descriptors ............................................................................................ 7
Self-Organizing Map .................................................................................................... 10
3. PATTERN EXTRACTION ..................................................................................................... 13
Overview ...................................................................................................................... 13
Image Acquisition ........................................................................................................ 14
viii
Graphical User Interface............................................................................................... 16
Image Standardization .................................................................................................. 17
Image Processing .......................................................................................................... 21
4. PATTERN RECOGNITION ................................................................................................... 26
Feature Extraction ........................................................................................................ 26
Descriptor 1: Spot Location.......................................................................................... 26
Descriptor 2: Hausdorff Dimension ............................................................................. 27
Descriptor 3: Elliptic Fourier Descriptors .................................................................... 30
Image Descriptor Matrix .............................................................................................. 31
Pattern Matching Overview .......................................................................................... 32
Classification by Self-Organizing Map ........................................................................ 33
Finding Matches ........................................................................................................... 35
5. RESULTS ................................................................................................................................ 38
Test Subjects ................................................................................................................. 38
Test Methods ................................................................................................................ 42
Testing Results ............................................................................................................. 42
6. DISCUSSION .......................................................................................................................... 45
Analysis ........................................................................................................................ 46
Future Work.................................................................................................................. 47
ix
Conclusion .................................................................................................................... 48
References ...................................................................................................................................... 49
x
LIST OF TABLES
Tables
Page
5.1 Matching test results for Group I (purple) and Group II (orange) ............................ 45
xi
LIST OF FIGURES
Figures
Page
1.1 FYLF captured in 2010 and again in 2011 .............................................................................. 3
1.2 The inputs and outputs of the primary components of the project and how they interact. ...... 5
2.1 The number '4' reconstructed by elliptic Fourier descriptors of orders 1, 2-10, 15, 20, 30, 40,
50, and 100 ....................................................................................................................................... 9
2.2 Hexagonal topology showing initial neighborhood relationship of neurons ......................... 10
2.3 Kohonen self-organizing map ................................................................................................ 12
3.1 Flowchart of GUI image standardization and processing algorithm. .................................... 13
3.2 Smartphone based system allows for the capture of images with consistent angle, distance,
and lighting .................................................................................................................................... 15
3.3 The main screen of the camera app ........................................................................................ 16
3.4 Using the reference points GUI, a user identifies the locations of standard reference points
for each imported image ................................................................................................................ 17
3.5 The image is rotated so that the bottom reference points make up the bottom two corners of
the cropped image .......................................................................................................................... 18
3.6 Cropping region is determined based on the location of the reference points. ...................... 20
3.7 Chin-spot images are scaled to a standard chin width, while maintaining their original aspect
ratio ................................................................................................................................................ 20
3.8 Progression of image processing algorithm ........................................................................... 23
xii
3.9 The edge of the chin is located using a Canny edge detector ................................................ 24
3.10 Continuation of the segmentation progression..................................................................... 25
4.1 Three location descriptors are defined as the ratios of distances from the reference points to
each spot’s centroid........................................................................................................................ 27
4.2 Hausdorff dimension of spots in a FYLF chin-spot image .................................................... 28
4.3 The box-counting algorithm .................................................................................................. 29
4.4 The slope of the best fit line approximates the Hausdorff dimension.................................... 29
4.5 Increasing harmonics improve the representation of the spot shape...................................... 31
4.6 The hexagonal neighborhood topology of the SOM .............................................................. 33
4.7 The images represents sample hits of data in the SOM ......................................................... 34
4.8 The image represents the weighted distances to neighboring neurons .................................. 35
4.8 Similar spots will be classified into the same, or near-by, neurons while dissimilar spots will
be classified into neurons that are farther away ............................................................................. 37
5.1 “Ada” ..................................................................................................................................... 39
5.2 “Bea” ...................................................................................................................................... 39
5.3 “Dax” ..................................................................................................................................... 40
5.4 “Eli” ....................................................................................................................................... 40
5.5 “Ray” ..................................................................................................................................... 41
5.6 “Sue” ...................................................................................................................................... 41
xiii
5.7 Simulated recaptures for Group I ........................................................................................... 43
5.8 Simulated recaptures for Group II ......................................................................................... 44
xiv
1
CHAPTER 1: INTRODUCTION
1.1
OVERVIEW
For many species, noninvasive photographic identification using natural markings
is an effective and efficient method for studying demographics of large wildlife
populations [2]. Natural markings have been used to identify individuals recaptured
across surveys and assist in the study of population dynamics for many species including
harbor seals [3], polar bears [4], sharks [5], and humpback whales [6]. An example of a
species that exhibits a unique natural marking is the Foothill Yellow-legged Frog (Rana
boylii, FYLF) of California. The FYLF is of interest to researchers because it is a
threatened species with a highly reduced range and also because of its role as an indicator
of overall ecosystem health [7], [8]. Annual field monitoring of the FYLF involves
catching, measuring, and photographing frogs before releasing them. Researchers with
the Center for Watershed Sciences at University of California, Davis as well as Garcia
and Associates have used spot patterns on the FYLF chins as a natural marker to identify
frogs that may be recaptured from year to year. Currently, this method involves manual
comparison of many hundreds of images within a database, which is time consuming,
inefficient, and potentially inaccurate.
This project aims to define and automate methods for capturing and processing
unique chin-spot pattern images and to find potential matches from a database of prior
samples. Techniques from image processing, pattern recognition and machine learning
are employed to efficiently and effectively identify potential recaptures of an individual
specimen.
2
1.2
WILDLIFE PATTERN MATCHING
Wildlife management and conservation efforts often rely on an understanding of
population demographics [9] developed by studying individual animals through time [3].
Photographs of unique natural markings can sometimes be used as a noninvasive way
[10] to identify animals without disturbing them [4]. Photographic identification of
individuals is an established technique [6], though underutilized because of the
difficulties involved in making positive visual identification in large data sets [5]. In
many cases, computer-aided identification of individuals through automated recognition
of natural markings provides a solution to this problem, e.g. [3], [6], [9]. While many
programs exist, they are generally highly targeted to unique features of the particular
species being studied, and algorithms are often not publically available [9].
Programs specifically designed for matching spot markings commonly use
algorithms adapted from astronomical pattern matching techniques [5], [9]. This method
involves forming triangles from selected triplets of point spots, and patterns are compared
by inspecting geometrically similar triangles [5]. While effective, this method requires
large numbers of spots to reliably find unique matches, and does not account for spot
shape. Additionally, commonly available systems require manual image processing to
correct for rotation and contrast variation [5], and they also require the user to
individually identify the most distinguishing features of each image [11]. This process is
not only time consuming when dealing with large numbers of images, but can also
introduce errors through selection of features and user biases.
3
Figure 1.1: FYLF captured in 2010 and again in 2011 (Garcia and Associates, 2012)
Researchers interested in the identification of FYLF individuals currently use
manual comparison of FYLF chin-spot patterns (Figure 1.1) to chronicle recaptures of
individuals over years of surveys [8]. There is currently no available program
specifically designed for identifying FYLF based on chin-spot patterns. Additionally,
from an assessment of the current literature, there does not appear to be a program that
accounts for both location and shape of identifying markings while requiring minimal
user input.
1.3
PROJECT OVERVIEW
In this project, we propose a procedure for capturing images of FYLF chin-spots
and automating a search for potential matches from a database of previously captured
images. The primary components of the project and the interactions between their inputs
4
and outputs are shown in Figure 1.2. An image capturing system that utilizes an Android
smartphone is used to collect chin-spot images that are standardized by angle, distance,
and lighting. A MATLAB-based graphical user interface (GUI) enables a user to
efficiently set reference points to identify a standard chin region. These reference points
are used to crop, scale, and rotate the chin-spot image. An image segmentation algorithm
then isolates the individual spots in the image to produce a binary image representing
only the spot pattern. The spot pattern is further reduced to a matrix of descriptors that
quantify the location and shape of each spot, which is then stored in a database. Matches
within the database are found by organizing spots into neighborhoods of similarity using
a self-organizing map (SOM) artificial neural network and a scoring algorithm to rank
image sets by similarity of spots and identify matches.
The remainder of this report is organized as follows. Chapter 2 covers background
on three of the key concepts used in the project: the Hausdorff dimension, elliptic Fourier
descriptors, and self-organizing maps. Chapters 3 and 4 discuss the methods used to first
capture, standardize, and segment FYLF chin spot images, and then quantify and search
for pattern matches to identify individuals. Chapter 5 details the methods and results used
to test the process. Chapter 6 is a discussion of the results and potential future
improvements.
5
Figure 1.2: The inputs and outputs of the primary components of the project and how
they interact.
6
CHAPTER 2: BACKGROUND
2.1
OVERVIEW
This chapter provides background information on three of the key concepts used
in our program. The Hausdorff dimension and the elliptic Fourier descriptors are used to
quantify individual spot shape. The self-organizing map (SOM) is used to group similar
chin-spot data prior to searching for matching patterns. The methods applied in our
pattern matching algorithm and discussed in Chapters 3 and 4 are based on the concepts
previewed below.
2.2
HAUSDORFF DIMENSION
The shape of individual chin-spots found on the FYLF can be described by the
degree of complexity of its boundary. Spots range from featureless elliptical spots, to
intricate, highly crenulated, and unique blobs. A useful quantifier of spot shape is the
Hausdorff dimension which is based on the fractal dimension of a shape [12]. Fractals
mathematically describe geometrical complexity that can model patterns in nature [13].
The fractal dimension is a metric that compares how the detail in a pattern changes with
the scale at which it is measured [12]. Fractal dimensions have been employed in pattern
recognition [14] as well as in quantifying irregular-shaped objects [15].
A technique for calculating the Hausdorff dimension is the box-counting
algorithm, which uses an aggregate of fractal dimension approximations. A grid of 𝑁
squares is superimposed over an image and the number of squares that touch the
boundary of the image, 𝑁𝑠 , is counted. The approximation is iteratively calculated for
7
decreasing box size, 𝑁. The resulting slope from the aggregate of the data is the boxcounting approximation of the Hausdorff dimension [16]
𝑑𝑖𝑚𝐻 =
2.3
ln⁡(𝑁𝑠 )
1
𝑁
ln⁡( )
.
(2.1)
ELLIPTIC FOURIER DESCRIPTORS
Elliptic Fourier descriptors were popularized by Khul and Giardina (1982) when
they introduced a method for finding the Fourier coefficients of a closed contour [17].
Their method allowed for a way of normalizing the Fourier coefficients using a harmonic
elliptic description of the contour or spot outline, making them invariant to rotation,
dilation, and translation without losing information about the shape of the contour [17].
Elliptic Fourier descriptors have been used in a variety of applications where
features need to be extracted from segmented or isolated shapes. In the field of
morphometrics, the “empirical fusion of geometry with biology” [18], elliptic Fourier
descriptors have been used to quantify the morphology of agricultural crops [19], [20]
and analyze fossils [21]. They have also been used in automatic pattern recognition
applications such as optical character recognition [1].
In Khul and Giardina’s method, a set of coefficients are found such that the
points, 𝑥(𝑡) and 𝑦(𝑡) (where 𝑡 = 1, … , 𝑚) of the closed contour can be approximated by,
𝑥̂(𝑡) = 𝐴0 + ⁡ ∑𝑁
𝑛=1 [𝑎𝑛 cos
𝑦̂(𝑡) = 𝐶0 + ⁡ ∑𝑁
𝑛=1 [𝑐𝑛 cos
2𝑛𝜋𝑡
𝑇
2𝑛𝜋𝑡
𝑇
+ 𝑏𝑛 sin
+ 𝑑𝑛 sin
2𝑛𝜋𝑡
𝑇
2𝑛𝜋𝑡
𝑇
],
(2.2)
],
(2.3)
8
where T is the total contour length and 𝑥(𝑡) ≡ 𝑥̂(𝑡)⁡, 𝑦(𝑡) ≡ 𝑦̂(𝑡) as 𝑁 → ∞.
The coefficients are found by,
1
𝑇
1
𝑇
𝐴0 = 𝑇 ∫0 𝑥(𝑡),
(2.4)
𝐶0 = 𝑇 ∫0 𝑦(𝑡),
1
𝑇
2𝑛𝜋𝑡
𝑎𝑛 = 𝑇 ∫0 𝑥(𝑡)cos⁡
1
(2.5)
𝑇
2𝑛𝜋𝑡
𝑏𝑛 = 𝑇 ∫0 𝑥(𝑡)sin⁡
𝑇
𝑇
2𝑛𝜋𝑡
1
𝑐𝑛 = 𝑇 ∫0 𝑦(𝑡)cos⁡
1
𝑇
𝑑𝑡,
(2.6)
𝑑𝑡,
(2.7)
𝑑𝑡,
(2.8)
𝑑𝑡.
(2.9)
𝑇
𝑇
2𝑛𝜋𝑡
𝑑𝑛 = 𝑇 ∫0 𝑦(𝑡)sin⁡
𝑇
The coefficients are dependent on the starting choice in the chain code of the contour, but
can be made independent by adjusting for the phase shift of the major axis. The phase
shift is found by
1
2(𝑎 𝑏 +𝑐 𝑑 )
𝜃1 = 2 𝑎𝑟𝑐𝑡𝑎𝑛 [𝑎2 +𝑐1 21−𝑏21−𝑑1 2 ]
1
1
1
(2.10)
1
and the rotation correction to the coefficients is then found by
[
𝑎𝑛∗
𝑐𝑛∗
𝑏𝑛∗
𝑎
]=[ 𝑛
𝑑𝑛∗
𝑐𝑛
to produce zero phase shift descriptors.
𝑏𝑛 cos 𝑛𝜃1
][
𝑑𝑛 sin 𝑛𝜃1
− sin 𝑛𝜃1
]
cos 𝑛𝜃1
(2.11)
9
Figure 2.1: The number '4' reconstructed by elliptic Fourier descriptors of orders 1, 2-10,
15, 20, 30, 40, 50, and 100 [1].
Rotation invariant descriptors are found from the rotation of the semi-major axis,
𝑐∗
𝜓1 = 𝑡𝑎𝑛−1 𝑎1∗ .
(2.12)
1
Rotating the descriptors by -⁡𝜓1 causes the semi-major axis to be parallel with the x-axis,
[
𝑎𝑛∗∗
𝑐𝑛∗∗
𝑏𝑛∗∗
cos 𝜓1
]=[
−sin 𝜓1
𝑑𝑛∗∗
sin 𝜓1 𝑎𝑛∗
][
cos 𝜓1 𝑐𝑛∗
𝑏𝑛∗
].
𝑑𝑛∗
(2.13)
Scale invariant features are found by dividing the coefficients by the magnitude of the
semi-major axis, E, found by
𝐸 = ⁡ √𝑎1∗2 + 𝑐1∗2 .
(2.14)
The lower order coefficients contain the most information about the character of
the shape [19] while higher orders provide more detail about minor features of the
contour. As the harmonic order is increased, the error between the original image and the
image reconstructed from the Fourier coefficients decreases. An example (Figure 2.1),
10
from a study by Trirt et al. [1] on optical character recognition shows the number ‘4’
reconstructed from elliptic Fourier descriptors at increasingly higher orders. While the
reconstruction improves dramatically between low order harmonics, there is little
improvement above the ninth harmonic.
2.4
SELF-ORGANIZING MAP
A self-organizing map is a type of artificial neural network model that can be used
to transform data of high-dimensionality into an array of neurons of low-dimensionality
[22], [23]. Neurons within a self-organizing map are arranged in networks connected via
adjacent neurons called neighborhoods (Figure 2.2). The connections between the
neurons are established according to weights that are adjusted to best match the input
Figure 2.2: Hexagonal topology showing initial neighborhood relationship of neurons.
The three colored regions are the first three neighborhoods surrounding the target
neuron located in the center. The area in red surrounding the target neuron is of size
zero. The green neighborhood surrounding the red area is neighborhood one. The blue
outermost neighborhood is neighborhood two (Adapted from Kohonen, 1990).
11
vector during the training process [24], [25] (Figure 2.3). A method of competitive,
unsupervised learning groups similar inputs within the SOM. Euclidean distance is
calculated between each input vector and weight vector during training. The neuron with
the smallest distance from each weight vector is considered the winner while all other
neurons are considered losing neurons. The weight associated with the winning neuron
along with the weights of all neighboring neurons are updated using the Kohonen
learning rule [25],
𝑖 𝑊(𝑘)
= ⁡ 𝑖𝑊(𝑘 − 1) + ⁡𝛼 𝑦𝑖 (𝑘)[𝑥(𝑘) − 𝑖𝑊(𝑘 − 1)],
(2.15)
𝑖⁡ ∈ ⁡ 𝑁𝑖 ∗ (𝑑),
(2.16)
𝑁𝑖 ∗ (𝑑) = ⁡ {𝑗, 𝑑𝑖𝑗 < 𝑑},
(2.17)
where 𝑖 contains the indices of all neurons within radius 𝑑 of the winning neuron 𝑖 ∗ , and
𝑁𝑖 ∗ (𝑑) is the neighborhood around winning neuron 𝑖 ∗ within radius 𝑑.
During training, the weights between neurons representing similar input
characteristics diminish while the weights between neurons representing dissimilar input
characteristics increase. This clustering of network inputs organizes inputs into
neighborhoods of similar characteristics. The fully trained network converges to weights
similar to training inputs and is capable of correctly classifying new inputs that were
represented in the training set [26].
12
Figure 2.3: Kohonen self-organizing map (Adapted from Fausett, 1994).
13
CHAPTER 3: PATTERN EXTRACTION
3.1
OVERVIEW
FYLF images are collected in the field using a system to standardize and annotate
the images. Next, the images are compiled using a Graphical User Interface (GUI)
created in MATLAB. The purpose of the GUI is to provide the user an interactive means
of identifying reference points necessary for image standardization. After the user selects
an image and reference points, the GUI performs automated image standardization and
image processing. The output of the GUI is a cropped, binary image that only contains
information about the chin-spot pattern (Figure 3.1).
Figure 3.1: Flowchart of GUI image standardization and processing algorithm.
14
3.2
IMAGE ACQUISITION
Image processing required to recognize and analyze patterns is simpler and more
accurate for images that are consistent. To detect and recognize FYLF chin-spots, it is
important to standardize the way that images are captured with regard to angle, lighting,
background, and distance from the camera.
The system developed for this project uses a camera-enabled smartphone as it is
an inexpensive source of hardware with the ability to capture images, display and input
information, write to storage, capture GPS information, and track date and time. To
enable and customize these features, we developed an application (app) for the Android
mobile operating system. The app allows a researcher in the field to input information
about the specimen and take a picture. The information as well as GPS location, date, and
time is recorded within the image metadata, enabling easy tracking of images.
A structure that enables consistent images was designed and built as described in
Leland and Gee [27]. The basic design includes a box with a fixture for the smartphone
on one side, LED lighting on the inside, and anti-reflective glass on the other side that the
frog can be gently pressed against (Figure 3.2).
Indirect foreground lighting, produced by placing LEDs between the camera and
the glass for specimen positioning, yielded the greatest contrast in the image without
causing glare on the glass. Background lighting, particularly from sunlight, was found to
degrade contrast. A black background with the specimen held by a hand in a black nitrile
glove provided excellent contrast with the lighter colored frog chin, making identifying
edges of the chin more consistent.
15
Figure 3.2: Smartphone based system allows for the capture of images with
consistent angle, distance, and lighting.
The Android app launches to a main screen that functions as the user interface for
inputting data relevant to the captured frog (Figure 3.3). The user is prompted to select
data on drop-down spinners with preloaded choices. This style of input interface allows
for simple and quick selection in the field and standardizes the file naming format.
The camera mode is set to auto focus, captures the image in a set orientation
regardless of camera orientation, and offers a simple interface for choosing to retake the
picture. By setting the camera to a fixed orientation, the image is stored in the same
orientation as other images, which facilitates pattern recognition and automated image
processing.
16
3.3
GRAPHICAL USER INTERFACE
The GUI is used to facilitate the identification of reference points and import
image information into the database. Upon launching the GUI, a file listing of recently
acquired frog images opens and allows the user to choose the desired image to prepare
for analysis. After an image is chosen, it is launched into the interactive screen of the
GUI (Figure 3.4). Inside the “Set Reference Points” box, three set buttons are available
for user interaction. The user selects each reference point, one at a time, following the
placement directions shown to the right of the buttons. The three reference points are
chosen to identify the tip of the frog's nose (reference point A), the leftmost corner where
the chin meets the shoulder (reference point B), and the rightmost corner where the chin
Figure 3.3: The main screen of the camera app. This app allows the user to enter
relevant information about the specimen (left) before positioning and capturing an
image (right).
17
Figure 3.4: Using the reference points GUI, a user identifies the locations of standard
reference points for each imported image.
meets the shoulder (reference point C). A cross-hair cursor appears to assist the user in
selecting correct locations with a high degree of accuracy. A “Clear” button is available if
the any points are incorrectly identified. After reference points have been defined, the
remaining GUI functions are automated and require no additional user interaction.
3.4
IMAGE STANDARDIZATION
The image standardization function accepts a captured frog image along with
user-defined reference points. The function first uses these reference points to remove
any rotation from the image. Next, the frog chin is cropped from the rest of the image by
18
a region bounded by the user-defined reference points. The coordinate locations of the
reference points are then translated to the cropped image coordinate space. Finally, the
image is scaled to a standard width.
Rotation may be introduced in the image either by user placement of the frog in
the capture device or by uneven placement of reference points due to frog anatomy. In
either case, it is imperative that the bottom two reference points be rotated to a plane
perpendicular to the vertical edge of the image (Figure 3.5). This leveling of the chin
provides a flat image base and maximizes the area captured by the bounding box formed
by the reference points in the cropping algorithm.
Rotation of the image is determined by comparing the two shoulder reference
points relative to one another. The image is rotated in the opposite direction making the
Figure 3.5: The image is rotated so that the bottom reference points make up the
bottom two corners of the cropped image.
19
shoulder reference points level. To maintain correct reference point location in the new
image, the distances from each reference point to the center of the image is calculated and
then transformed to polar measurements. The image angle of rotation is combined with
the angle of each point and the coordinates are transformed back to Cartesian coordinates
of the rotated image. The resulting image is free from any rotation, with the two shoulder
points perpendicular to the vertical edge of the image. The new locations of the reference
points are passed to the cropping function.
Cropping the image isolates the chin of the frog by removing a majority of the
unnecessary features of the frog as well as the background of the image. In creating an
image that mostly contains the chin-spot pattern, the image processing is less prone to
error due to extreme values that could be present in a larger image. An image that is
reduced in size also requires less time for image processing and reduces the likelihood of
incorrectly segmenting non-spot features in the image.
The three reference points define the boundary of the cropping area (Figure 3.6).
The top reference point determines the upper horizontal constraint, the left shoulder
determines the left vertical constraint, and the right shoulder determines the lower
horizontal and right vertical constraint.
The cropped image is scaled to make the chin-spot image invariant to size (Figure
3.7). All images are set to a fixed width of 350 pixels and a length of N pixels. The length
N of the image is any amount required to retain the original aspect ratio of the original
image. By constraining the width of the chin images, the location and size of spots in the
image remain similar regardless of the size of the frog throughout its life cycle. This
20
Figure 3.6: Cropping region is determined based on the location of the reference
points.
Figure 3.7: Chin-spot images are scaled to a standard chin width, while maintaining
their original aspect ratio.
21
constraint is also useful during image processing and in normalizing the spot-descriptor
training data in preparation for pattern matching.
3.5
IMAGE PROCESSING
The image processing function is an adaptive algorithm that accepts a cropped
and scaled color image of the frog chin and reduces it to a binary image containing only
spots. The algorithm employs three main image processing techniques to segment the
image: histogram equalization, edge detection, and morphology.
Histogram equalization is a technique that improves the contrast in a grayscale
image by centering an average pixel value in the range of gray values and expands the
range of pixel values to extend to the upper and lower displayable limits [28]. Histogram
equalization is performed twice in the segmentation algorithm. It first improves the
contrast between the specimen and the background prior to edge detection and, second,
improves the contrast between the specimen’s chin and spots prior to thresholding.
Increased contrast exaggerates edges in an image and helps standardize variation in
darkness of spots.
Edge detection is used to isolate the portion of the image that contains the
specimen’s chin from the background. The chin is outlined by first applying a Canny
edge detector to find the dominant edges in the image. This involves first applying a lowpass smoothing filter followed by a calculation of the gradient [28]. The result is a binary
image that shows the outline of the specimen’s chin and the outlines of the spots within
the chin. In order to differentiate between the edge of the chin and the edge of the spots,
the pixel in each row closest to the specimen’s nose is kept while all other pixels are
22
discarded. The result is a line that primarily traces the edge of the chin but diverges when
spots appear at the very edge of the chin. Given these divergences typically appear as
high frequency jumps away from the actual chin edge, the edge can be approximated by
applying a low-pass filter to the line followed by fitting an eighth order polynomial to the
filtered line (Figure 3.8). The result is a reliable detection of the edge of the specimen
chin.
The third primary technique, morphology, is used to clean up the binary spots
image after thresholding with the objective of removing small artifacts and incorrectly
connected segments. Morphological operations are used to change the shape of a binary
object by convolving the image with a structuring element to produce an output that
depends on the operation used [28]. Two primary operations are used; erosion and
dilation. Erosion returns an output that represents instances where the structuring element
is completely contained in the image, which has the effect of deleting features smaller
than the structuring element. Dilation returns an output that represents instances where
the structuring element intersects the image, which has the effect of expanding the shapes
in the image.
The sequence of the algorithm is as follows (Figures 3.8, 3.9, and 3.10):
1. Convert cropped color chin image (A) to grayscale (B).
2. Improve contrast of grayscale image (B) by histogram equalization (C).
3. Find edges in image (B) using the Canny edge detector (D).
4. Keep left-most pixel as chin edge (E).
23
Figure 3.8: Progression of image processing algorithm. (A) Starting image, (B)
conversion to grayscale, (C) improve contrast, (D) find edges, (E) locate left-most
edges.
5. Smooth chin edge using a low-pass filter and then straighten by fitting it to a
polynomial function (Figure 3.9).
6. Remove portion of the image to the left of the approximated chin line (F).
7. Improve contrast between the spots and chin by histogram equalization (G).
8. Convert the image to a binary representation by thresholding (H).
9. Separate connected spots and remove small artifacts through dilation with a discshaped structuring element (I).
10. Erode with a disc-shaped structuring element to fill out and expand the spots (J).
24
11. The compliment of the image represents the spots as ones and the rest as zeroes
(K).
The use of histogram equalization to improve the contrast allows this method to adapt
to some changes in lighting conditions as well as differences in spot color and contrast. It
Figure 3.9: The edge of the chin is located using a Canny edge detector (black line).
Variation in the edge line is smoothed using a low-pass filter (red line) and the chin
outline is approximated by fitting it to a polynomial function (green line).
25
Figure 3.10: Continuation of the segmentation progression. Chin is isolated (F),
contrast is improved (G), image is thresholded (H), spots are eroded (I), spots are
dilated (J), and compliment of image is found (K).
has been observed that the clarity of the FYLF individual’s spot pattern can change from
year to year [29] and this algorithm is effective at segmenting both variations in spot
contrast between specimens as well as within a single specimen. Challenges include
selecting an appropriate structuring element size for the morphological operations. A
structuring element that is too small has the potential to leave spots connected when they
should not be connected, particularly around the edges. If the structuring element is too
large it can remove too much of the spot characteristics.
26
CHAPTER 4: PATTERN RECOGNITION
4.1
FEATURE EXTRACTION
The feature extraction algorithm takes the binary, segmented spots image from the
image processing algorithm and converts it to a set of numerical descriptors that represent
features of each of the spots in the image. For each spot in an image, a vector of 40
descriptors is generated that describes the location and shape of the spot. The first three
descriptors represent ratios that describe the location of the centroid of the spot in relation
to the three reference points set by the GUI. The next descriptor uses the Hausdorff
dimension to describe the complexity of the spot boundary. Finally, a set of 36 elliptic
Fourier coefficients describe a nine-harmonic general function of the spot boundary.
These sets of descriptors represent a unique quantification of the characteristics of each
spot, which is later used to identify matches.
4.2
DESCRIPTOR 1: SPOT LOCATION
Location descriptors are created by comparing the location of the centroid of the
spot to the location of the three reference points set in the GUI. The distance between the
centroid and each reference point is found (Figure 4.1). Three location descriptors are
then found by,
𝐷1 =
𝑫𝒊𝒔𝒕⁡𝑨
𝑫𝒊𝒔𝒕⁡𝑩
𝐷2 =
𝑫𝒊𝒔𝒕⁡𝑨
𝑫𝒊𝒔𝒕⁡𝑪
𝐷3 =
𝑫𝒊𝒔𝒕⁡𝑩
𝑫𝒊𝒔𝒕⁡𝑪
27
Figure 4.1: Three location descriptors are defined as the ratios of distances from the
reference points to each spot’s centroid.
Dividing one distance by the other normalizes the descriptor making it unitless and
invariant to scale.
FigureD4-2
4.3
ESCRIPTOR 2: HAUSDORFF DIMENSION
The complexity of the perimeter of an individual spot is quantitatively calculated
using
the4-3
Hausdorff dimension. A Hausdorff dimension of 𝑑𝑖𝑚𝐻 = 1 represents a
Figure
smooth line while a dimension of 𝑑𝑖𝑚𝐻 = 2 represents high fractal complexity.
Individual spot complexity is bounded by these two extremes and is represented as a
decimal value defined over the interval⁡1 < 𝑑𝑖𝑚𝐻 < 2 (Figure 4.2). Since spot perimeter
complexity varies greatly between spot to spot, the Hausdorff dimension is a useful shape
descriptor.
28
Figure 4.2: Hausdorff dimension of spots in a FYLF chin-spot image. Red spots show
elongated narrow spots with low Hausdorff dimension, while blue spots show
rounded spots with higher Hausdorff dimension.
The Hausdorff dimension is calculated using the box-counting algorithm in which
a zero-padded image containing an individual spot is initially represented by a box of
size⁡𝑠, the size of the image. The box count 𝑁𝑠 containing any part of the spot perimeter
is recorded. On the next iteration, the size of 𝑠 is set to
𝑠
2
, and the number of boxes of the
image, 𝑁, increases. Again, the box count, 𝑁𝑠⁡ containing parts of the spot perimeter is
recorded (Figure 4.3). This pattern repeats until 𝑠 becomes so small that it can no longer
be represented due to the constraint of pixel size. The log of the number of blocks, ln(𝑁),
and the log of the box count, ln(𝑁𝑠 ), of each iteration are compared and a least-squares
best fit is calculated to describe the slope of the data (Figure 4.4). The
29
Figure 4.3: The box-counting algorithm. The image on the left shows an early
iteration of the box-counting algorithm with 𝑁 = 28 and 𝑁𝑠⁡ = 18 resulting in a
Hausdorff dimension of 1.153. The image on the right shows a later iteration of the
same image with 𝑁 = 112 and 𝑁𝑠⁡ = 44 resulting in a Hausdorff dimension of 1.246.
Figure 4.4: The slope of the best fit line approximates the Hausdorff dimension.
Multiple iterations of the number of blocks, ln(𝑁), plotted against the box "hits",
ln(𝑁𝑠 ).
30
resulting slope from the aggregate of the data is the box-counting approximation of the
Hausdorff dimension.
4.4
DESCRIPTOR 3: ELLIPTIC FOURIER DESCRIPTORS
The Fourier coefficients of a chain code representation of the spot contours are
used as shape descriptors. The elliptic Fourier descriptors (EFDs) are generated using a
function adapted from work by David Thomas from the University of Melbourne [30].
An x-y representation of the outline of a single spot is standardized to a common rotation
and scale and the four Fourier coefficients are calculated for each harmonic as described
in Chapter 2. The result is 4 × 𝑁 numbers that describe the shape of the spot in the form,
𝑎1 , 𝑎2 , 𝑎3 … 𝑎𝑁 ,
𝑏1 , 𝑏2 , 𝑏3 … 𝑏𝑁 ,
𝑐1 , 𝑐2 , 𝑐3 … 𝑐𝑁 ,
𝑑1 , 𝑑2 , 𝑑3 … 𝑑𝑁 .
It was found that nine harmonics, N = 9, yielded an acceptable compromise
between representation of the shape and generality between the descriptors. Figure 4.5
illustrates three different representations of the FYLF spot (black line) reconstructed from
their EFDs. The blue line shows a reconstruction of the second harmonic, N = 2, which is
a simple ellipse. The yellow line, the fourth harmonic, N = 4, is a general representation
of the spot contour but lacks much of the detail that may differentiate this spot from
others. The red line is the reconstruction of the first nine harmonics, N = 9. While this
representation generalizes some of the small contours in the shape, the important features
31
Figure 4.5: Increasing harmonics improve the representation of the spot shape.
of the spot are captured. For each spot in an image set, 36 coefficients, or nine sets of
four coefficients, are extracted and passed to the database as spot shape descriptors.
4.5
IMAGE DESCRIPTOR MATRIX
The complete set of descriptors for each spot in an image is associated with the
specimen they originated from and stored in a matrix. Linking the individual spots to
their original image allows the descriptor matrix for an image to be combined with
descriptor matrices from other images without losing track of their origin. As images are
32
imported through the Reference Points GUI, descriptors are found for each spot and
combined into a 𝑁𝑠𝑝𝑜𝑡𝑠 × 40 matrix and stored as a ‘.mat’ file.
The resulting matrix is a set of descriptors that describe the location and shape of
each spot that makes up the image set. This image descriptor matrix can then be used to
identify similar sets of descriptors of spots that have similar location and shape
characteristics.
4.6
PATTERN MATCHING OVERVIEW
Using a database of image descriptor matrices, we developed an algorithm to
search for matches. The basic method used to group likely matches based on similarities
in each image descriptor matrix is as follows. First, all the matrices are combined and
outlier spots are removed from the matrix. Next, similar spots are grouped together by a
self-organizing map. Finally, a scoring system is used to rank the similarity of image sets
and identify potential matches.
The image descriptor matrices for all the images being matched are combined into
a single comprehensive matrix. Outliers are identified and removed by eliminating spotdescriptor sets with features that are outside of ±⁡4𝜎 of the mean for each type of
descriptor. These outlier spots are commonly artifacts generated during the image
segmentation process and have the effect of skewing the distribution of the selforganizing map. This complete matrix is then passed to the neural network for
classification.
33
4.7
CLASSIFICATION BY SELF-ORGANIZING MAP
A self-organizing map (SOM) is set up using the Neural Network Clustering
toolbox in MATLAB. A single layer, two-dimensional map consisting of 900 neurons in
a 30x30 hexagonal neighborhood configuration is used (Figure 4.6).
The input data for the SOM are the 40 descriptor values of each spot’s descriptor
set. The output of the SOM is a single neuron, among a group of 900, which represents a
possible location for each spot. Spots that are identical are represented by the same
neuron with similar spots grouped in neighborhoods of neurons that are close in
proximity to one another (Figure 4.7). Conversely, spots that are dissimilar are
represented in neurons that are separated by a large distance.
Figure 4.6: The hexagonal neighborhood topology of the SOM. As training is
performed, the weights are updated and the distances and general shape of the network
will change.
34
Figure 4.7: The images represent sample hits of data in the SOM. The number and size
of the blue hexagon represent the number of data points associated with each neuron.
The map on the left represents the SOM after just one iteration while the map on the
right represents the SOM after 200 iterations.
The SOM is trained using a batch add algorithm where the entire image descriptor
matrix of each FYLF is added to the SOM for initial training. Each spot’s descriptor set is
then run through a competitive learning layer until all spots have been processed. The
SOM then updates the weights of all neurons based on the results of the competitive
learning layer at the end of each iteration, or epoch. Clustering is very general after just a
few epochs and more clearly classified after many epochs.
Figure 4.8 illustrates the iterative process of the self-organizing map toolbox in
MATLAB. The map on the left represents neighborhood distances after a single iteration
has been completed. It shows that many iterations produce the more evenly distributed
data throughout the map, which is important for improving classification. Classification
is very general in this case; the dark red line represents a clear distinction between the left
and right side of the map, meaning that the neurons are weighted much further apart,
35
Figure 4.8: The images represent the weighted distances to neighboring neurons. The
small blue hexagons represent the neurons; the red lines show the connections between
neighboring neurons. The colors in the regions containing the red lines represent the
distance between neurons. Black and dark red represent the furthest distances, while
orange and yellow represent smaller distances.
creating just two main classes of spots. A small cluster in the top left of the map can be
seen forming that marks the beginnings of classification of a spot. The map on the right
represents neighborhood distances after 200 iterations. Very obvious clusters have
formed and the initial general classification after a single iteration has been refined to
form more exact classification throughout the map.
4.8
FINDING MATCHES
With individual spots clustered with similar spots by the SOM, complete FYLF
images can be matched by relating similar spots. Each spot, represented by a descriptor
vector, is associated with a neuron by identifying the closest weight vector to the
descriptor vector. The following algorithm structure is used to find similar sets of spots
that make up an image.
36
1. An image matrix, consisting of a collection of spots from individual images
classified into neurons, is compared to the complete collection of image matrices.
2. For each spot in the original image set:
a. All spots that exist in the same neuron award a point to their image set.
b. All spots that exist in adjacent neurons are considered.
c. Adjacent spots’ image sets are assigned a weighted point based on their
distance from the original spot’s neuron scaled using a Gaussian function
(Figure 4.9).
d. This is repeated for each spot in the original image set and a tally is
maintained for all other image sets.
3. The most similar image sets are the sets with the highest final score.
This method relies on the self-organizing map’s ability to group spots with
similar location and shape features into the same or adjacent neurons. The method works
well, but is sensitive to the size of the map. If the map consists of too few neurons, then
spots with a lot of variation are grouped together, resulting in higher numbers of false
positive matches. If the map is too large then spots that are very similar could be placed
in neurons outside of clustered neighborhoods, increasing the likelihood of missed
matches. A possible way to improve the performance of the matching algorithm for very
large maps would be to consider a larger neighborhood beyond just the six adjacent
neurons. This would give a higher score to image sets with similar spot patterns, but also
might increase the likelihood of false positives. The effectiveness of this method can also
37
Figure 4.9: Similar spots will be classified into the same, or near-by, neurons while
dissimilar spots will be classified into neurons that are farther away.
be tuned by changing the standard deviation of the Gaussian function that scales the score
given to image set spots found in adjacent neurons.
New images can be added to the database by running them through the Reference
Points GUI, image segmentation, and feature extraction. To perform a new search, the
descriptor sets are recombined, outliers are removed, the SOM is retrained, and the
matching algorithm rescores the similarity of spot sets.
38
CHAPTER 5: RESULTS
5.1
TEST SUBJECTS
A set of rubber model frogs were created by copying chin-spot patterns from
archived photos of field-captured Foothill Yellow-legged Frogs (FYLFs). An artificial set
of model frogs was chosen over a real set for several reasons. First, FYLFs are in
hibernation during the winter months so fieldwork is done in the summertime. Since the
project development occurred in the late fall, winter, and early spring, the models were
employed for prototype development, which could be then tested in the field during the
next field season. Second, the dynamic nature of developing and testing a project
involves extensive designing, and often redesigning, of hardware and algorithms. Using a
replica set of frogs avoids unnecessary handling of and stress to living animals. Finally,
by creating a set of model frogs we can control the type of variation in spot patterns
among the population of test frogs.
Chin-spot patterns were recreated by hand as accurately as possible to realistically
represent the model frogs (Figures 5.1-5.6). A sample set of six frogs were chosen from
archived photos containing two groups of three frogs each. The first group (Group I)
contains three frogs with distinctly varying spot shapes in locations uniformly placed on
the chin. The second group (Group II) contains three frogs with nondescript, generally
oval spot shapes in locations closer to the lip of the frog. These two groups simulate
variability that is expected in chin-spot patterns.
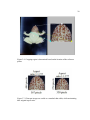
39
Figure 5.1: “Ada” – Field image (left) (Ryan Peek, 2013), close-up of chin-spot pattern
(top right), and rubber frog replica (bottom right).
Figure 5.2: “Bea” – Field image (left) (Ryan Peek, 2013), close-up of chin-spot
pattern (top right), and rubber frog replica (bottom right).
40
Figure 5.3: “Dax” – Field image (left) (Ryan Peek, 2013), close-up of chin-spot
pattern (top right), and rubber frog replica (bottom right).
Figure 5.4: “Eli” – Field image (left) (Ryan Peek, 2013), close-up of chin-spot pattern
(top right), and rubber frog replica (bottom right).
41
Figure 5.5: “Ray” – Field image (left) (Ryan Peek, 2013), close-up of chin-spot
pattern (top right), and rubber frog replica (bottom right).
Figure 5.6: “Sue” – Field image (left) (Ryan Peek, 2013), close-up of chin-spot
pattern (top right), and rubber frog replica (bottom right).
42
5.2
TEST METHODS
The objective of testing is to simulate multiple captures of each individual frog
and test the system’s ability to identify matches from a collection of related and unrelated
images. Multiple captures were simulated by taking four different images of each
specimen and labeling them with test years “1992” through “1995”. Variations in the
positioning and rotation between each simulated capture year were introduced by
removing and repositioning the specimen between capturing each image (Figures 5.7 and
5.8). Importing images in the Reference Points GUI generates an image descriptor matrix
for each individual frog image. Using this matrix as a training set, spots are then clustered
by similarity using the self-organizing map and matching with the matching algorithm is
performed.
5.3
TESTING RESULTS
The results of the matching test for Group I are shown in purple and in orange for
Group II (Table 5.1). Matching was done by comparing a single image set to all of the
image sets in the database and returning the highest scoring results. A perfect match
returns a positive match for the original image as well as three images for the other three
simulated years. The results tables show the number of correct matches returned as well
as the number of false positive and expresses both of these quantities as a percentage of
the total possible.
The results show that the pattern matching algorithm is very effective at
determining matches when the samples have a high number of spots with unique shapes.
Group I is associated with a perfect record of success in finding the correctly matching
43
Figure 5.7: Simulated recaptures for Group I containing “Ada”, “Bea”, and “Dax”.
images. However, the system was much less effective at finding correct matches among
images with lower numbers of similarly shaped spots. Group II had an average success
rate of only 63% with some images matching with only 25% accuracy, indicating that a
single image found only itself.
44
Figure 5.8: Simulated recaptures for Group II containing “Eli”, “Ray”, and “Sue”.
45
Table 5.1: Matching test results for Group I (purple) and Group II (orange).
46
CHAPTER 6: DISCUSSION
6.1
ANALYSIS
The foundation for an effective method for capturing and matching FYLF
individuals through image pattern recognition was demonstrated. The image acquisition
and standardization system allows researchers to capture useful images and gives them
the ability to easily store important information with the image. The Reference Points
GUI, along with the image processing and spots segmentation algorithms, enables
efficient extraction of descriptive features from FYLF chin-spot images.
Testing results highlighted an anticipated inconsistency in the performance of the
identification algorithm. The differences in results can be attributed to the difference
between the two categories of spots present in the test groups. In Group I, spots generally
show strong variation in morphology and are easily recognizable by shape. In Group II,
successfully segmented spots generally show a tendency toward morphological similarity
with chin-spot pattern uniqueness expressed more through location of spots.
The preference toward recognition of spot shape over spot location is apparent
when considering the descriptor matrix used to train the self-organizing map. Of the 40
descriptor elements, 37 are associated with shape characteristics of the spots. This has the
effect of reducing the influence of location descriptors. Spots that are fundamentally
elliptical in shape can be effectively represented by a small set of elliptic Fourier
descriptors. This results in very little information defining the shape of the spot being
contained within the higher harmonics. The self-organizing map groups these spots in a
way that distinguishes them from spots with complex shapes, but does not make them
47
unique amongst themselves.
Using additional descriptors that are more representative of location features
could improve the defining of spots without unique shape features. Alternatively, more
importance can be given to location descriptors in the descriptor set. By adding location
descriptors, or increasing importance of location descriptors, the resulting identification
algorithm would be expected to perform with higher accuracy.
Another factor affecting the performance of the Group II is the effectiveness of
the spot segmentation algorithm. Many of the distinctive spot features from Group II are
located on the edge of the chin. Due to how the image processing is performed, features
at the very edge of the chin have a tendency to be poorly defined and, as a result, are
often segmented together as a large clump. These clumps of spots are not useful for
identification and are typically discarded during the outlier removal step prior to training
the self-organizing map. With the edge spots removed, a match must be made based on a
small number of generally nondescript spots from the center of the chin, resulting in less
reliable identification.
6.2
FUTURE WORK
There are a number of improvements that could be made to advance this method
for identifying FYLF individuals from images and extend the understanding of its
feasibility as a tool for studying species population dynamics. First, an improvement to
the segmentation algorithm could improve the viability of spot patterns at the very edge
of the chin. Optimization of contrast improvement could be used to distinguish the chin
edge from the spot, and specialized structuring elements used during the morphological
48
operations could improve separation of spots. Furthermore, classification of spots could
be improved by increasing the importance of spot location compared to spot shape, as
previously discussed. This could potentially be done through a weighting system that
gives preference to some elements of an input over others, or by modifying the learning
rules that effect how final neuron locations are determined. In addition to altering the
learning rules of the self-organizing map, optimization can be achieved through
experimentation with the size of the map and number of iterations used to train it. Finally,
this system should be tested with real FYLFs and modifications should be made to
accommodate any new elements added. While effort was made to recreate artificial
models that closely represented their real life counterparts, there are differences that
could affect the effectiveness of segmentation. Relatively simple optimization of the
image processing algorithm could significantly improve its performance in real world
applications.
6.3
CONCLUSION
A novel method for identifying FYLF individuals based on chin-spot pattern
recognition is presented. The method is shown to be effective for certain types of spot
patterns and improvements are suggested to enhance its ability to identify a larger variety
of patterns. The process discussed can be used to help researchers understand the
dynamics of FYLF populations in a relatively non-invasive manner with the goal of
better understanding the species as well as its associated ecosystems.
49
References
[1]
Ø. Due Trier, A. K. Jain, and T. Taxt, "Feature extraction methods for character
recognition - a survey," Pattern Recognition, vol. 29, pp. 641-662, 1996.
[2]
T. A. Morrison, J. Yoshizaki, J. D. Nichols, and D. T. Bolger, "Estimating
survival in photographic capture–recapture studies: overcoming misidentification
error," Methods in Ecology and Evolution, vol. 2, pp. 454-463, 2011.
[3]
K. K. Hastings, L. A. Hiby, and R. J. Small, "Evaluation of a computer-assisted
photograph-matching system to monitor naturally marked harbor seals at Tugidak
Island, Alaska," Journal of Mammalogy, vol. 89, pp. 1201-1211, 2008.
[4]
C. J. R. Anderson, N. d. V. Lobo, J. D. Roth, and J. M. Waterman, "Computeraided photo-identification system with an application to polar bears based on
whisker spot patterns," 2010.
[5]
Z. Arzoumanian, J. Holmberg, and B. Norman, "An astronomical pattern‐
matching algorithm for computer‐aided identification of whale sharks Rhincodon
typus," Journal of Applied Ecology, vol. 42, pp. 999-1011, 2005.
[6]
E. Kniest, D. Burns, and P. Harrison, "Fluke Matcher: A computer-aided
matching system for humpback whale (Megaptera novaeangliae) flukes," Marine
Mammal Science, 2009.
[7]
S. M. Yarnell, C. Bondi, A. J. Lind, and R. A. Peek, "Habitat models for the
foothill yellow-legged frog (rana boylii) in the sierra nevada of california," 2011.
50
[8]
Garcia and Associates, "Foothill Yellow-legged Frog monitoringat little carson
creek and big carson creek, mt. Tamalpais watershed, fall 2009 to fall 2011,"
2012.
[9]
C. W. Speed, M. G. Meekan, and C. J. Bradshaw, "Spot the match–wildlife
photo-identification using information theory," Frontiers in Zoology, vol. 4, pp. 111, 2007.
[10]
M. J. Kelly, "Computer-aided photograph matching in studies using individual
identification: an example from Serengeti cheetahs," Journal of Mammalogy, vol.
82, pp. 440-449, 2001.
[11]
J. d. Hartog and R. Reijns, "I3S Manta Manual," ed, 2008.
[12]
D. Schleicher, "Hausdorff dimension, its properties, and its surprises," The
American Mathematical Monthly, pp. 509-528, 2007.
[13]
P. Maragos and F.-K. Sun, "Measuring the fractal dimension of signals:
morphological covers and iterative optimization," IEEE Transactions on signal
Processing, vol. 41, pp. 108-121, 1993.
[14]
D. Barbará and P. Chen, "Using the fractal dimension to cluster datasets," in
Proceedings of the sixth ACM SIGKDD international conference on knowledge
discovery and data mining, 2000, pp. 260-264.
[15]
J. Orford and W. Whalley, "The use of the fractal dimension to quantify the
morphology of irregular‐shaped particles," Sedimentology, vol. 30, pp. 655-668,
1983.
51
[16]
P. Duvall, J. Keesling, and A. Vince, "The Hausdorff dimension of the boundary
of a self-similar tile," Journal of the London Mathematical Society, vol. 61, pp.
748-760, 2000.
[17]
F. P. Kuhl and C. R. Giardina, "Elliptic Fourier features of a closed contour,"
Computer Graphics and Image Processing, vol. 18, pp. 236-258, 1982.
[18]
F. L. Bookstein, "Foundations of Morphometrics," Annual Reviews of Ecology
and Systematics, vol. 13, pp. 451-470, 1982.
[19]
P. Lootens, J. Van Waes, and L. Carlier, "Description of the morphology of roots
of Chicorium intybus L. partim by means of image analysis: Comparison of
elliptic Fourier descriptors and classical parameters," Computers and Electronics
in Agriculture, vol. 58, pp. 164-173, 2007.
[20]
H. Mebatsion, J. Paliwal, and D. Jayas, "Evaluation of variations in the shape of
grain types using principal components analysis of the elliptic Fourier
descriptors," Computers and Electronics in Agriculture, vol. 80, pp. 63-70, 2012.
[21]
J. S. Crampton, "Elliptic Fourier shape analysis of fossil bivalves: some practical
considerations," Lethaia, vol. 28, pp. 179-186, 1995.
[22]
T. Kohonen, "The self-organizing map," Proceedings of the IEEE, vol. 78, pp.
1464-1480, 1990.
[23]
T. Kohonen, E. Oja, O. Simula, A. Visa, and J. Kangas, "Engineering applications
of the self-organizing map," Proceedings of the IEEE, vol. 84, pp. 1358-1384,
1996.
52
[24]
J. Vesanto, J. Himberg, E. Alhoniemi, and J. Parhankangas, "Self-organizing map
in Matlab: the SOM Toolbox," in Proceedings of the Matlab DSP conference,
1999, pp. 16-17.
[25]
L. Fausett, Fundamentals of Neural Networks: Architectures, Algorithms, and
Applications: Prentice-Hall, Inc., 1994.
[26]
M. U. s. Guide, "The Mathworks," Inc., Natick, MA, vol. 5, 1998.
[27]
O. K. Leland and N. E. Gee, "A System for Capturing and Annotating
Standardized Images of Foothill Yellow Legged Frogs," 2014.
[28]
R. Szeliski, Computer Vision: Algorithms and Applications. Ithaca, NY: Springer,
2011.
[29]
R. Peek, "Personal Comunication," ed, 2013.
[30]
D. Thomas. (2006). Elliptical Fourier Shape Descriptors. Available:
http://www.mathworks.com/matlabcentral/fileexchange/12746-elliptical-fouriershape-descriptors