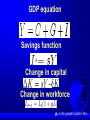Download LEC2

The Neoclassical Growth Model
Dr. Imtithal AL-Thumairi
Webpage:http://www-users.york.ac.uk/~iaat100/
The Exogenous growth model, also known as
the Neo-classical model or Solow growth model
is a term used to sum up the contributions of
various authors to a model of long-run economic
growth within the framework of neoclassical
economics.
The most important contribution was probably
the work done by Robert Solow; in 1956, Solow
and T.W.Swan. developed a relatively simple
growth model which fit available data on US
economic growth with some success. Solow
received the 1987 Nobel Prize in Economics for
his work on the model.
Solow extended the HarrodDomar model by:
Adding labour as a faactor of
production;
Requiring diminishing returns to labour
and capital separately, and constant
returns to scale for both factors
combined;
Introducing a time-varying technology
variable distinct from capital and labor.
Short run implications
Policy measures like tax cuts or investment subsidies
can affect the steady state level of output but not the
long-run growth rate.
Growth is affected only in the short-run as the
economy converges to the new steady state output
level.
The rate of growth as the economy converges to the
steady state is determined by the rate of capital
accumulation.
Capital accumulation is in turn determined by the
savings rate (the proportion of output used to create
more capital rather than being consumed) and the
rate of capital depreciation.
Long run implications
In neoclassical growth models, the long-run
rate of growth is Exogenously determined - in
other words, it is determined outside of the
model. A common prediction of these models
is that an economy will always converge
towards a steady state rate of growth, which
depends only on the rate of technological
progress and the rate of labor force growth.
A country with a higher saving rate will
experience faster growth, e.g. Singapore had
a 40% saving rate in the period 1960 to 1996
and annual GDP growth of 5-6%, compared
with Kenya in the same time period which
had a 15% saving rate and annual GDP
growth of just 1%.
Assumptions
Capital is subject to diminishing returns.
Given a fixed stock of labor, the impact
on output of the last unit of capital
accumulated will always be less than
the one before.
Empirical evidence
A key prediction of neoclassical growth
models is that the income levels of poor
countries will tend to catch up with or
converge towards the income levels of rich
countries.
The evidence is stronger for convergence
within countries. For instance the per-capita
income levels of the southern states of the
United States have tended to converge to the
levels in the Northern states.
Criticisms of the model
failure to take account of other issues can
affect economic growth as the strength of
institutions (which facilitate economic growth).
it does not explain how or why technological
progress occurs
This failing has led to the development of
endogenous
growth
theroy,
which
endogenizes technological progress and/or
knowledge accumulation.
Graphical representation of the model
The model starts with a
neoclassical production
function Y/L = F(K/L),
rearranged to y = f(k), which
is the orange curve on the
graph. From the production
function; output per worker is
a function of capital per
worker. The production
function assumes
diminishing returns to capital
in this model, as denoted by
the slope of the production
function.
The model and changes in the saving rate
an increase in the saving
rate shifts the function up.
Saving per worker is now
greater
than
population
growth plus depreciation, so
capital
accumulation
increases, shifting the steady
state from point A to B.
output
per
worker
correspondingly moves from
y0 to y1.
The model and changes in population
the population has now
increased from n to n1
The production function and
the saving rate do not
change
As there is now a bigger
labour force, but the same
amount
of
investment
(saving), saving per worker
decreases, and therefore the
steady state shifts down from
A to B.
Capital per worker has
decreased from k0 to k1,
saving per worker has
decreased from sy0 to sy1,
and output per worker has
correspondingly decreased
from y0 to y1
Mathematical framework
The Solow growth model can be described
by the interaction of five basic
macroeconomic equations:
Macro-production function
GDP equation
Savings function
Change in capital
Change in workforce
Macro-production function
This is a Cobb-Douglas function where
Y represents the total production in an
economy. A represents multifactor
productivity (often generalized as
technology), K is capital and L is labour.
GDP equation
Savings function
Change in capital
Change in workforce
gL is the growth function for L.