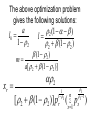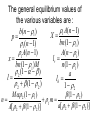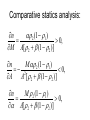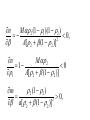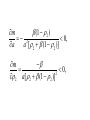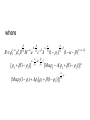* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 2005314134057165
Survey
Document related concepts
Transcript
Increasing Returns and
Economic Efficiency
More Seriously
• Learning costs, indivisibilities giving rise
to sizable fixed costs. Information and
knowledge in production makes IR
prevalent (Wilson 1975, Radner &
Stiglitz 1984, Arrow 1995).
• Empirical evidence for IR (Ades &
Glaeser 1999, Antweiler & Trefler 2002).
IR and Economic Analysis
• Largely ignored in the core, esp. in GE
analysis.
• Frequently discussed in IO, development
economics, international trade.
• Surveys: Yang & S. Ng (1998); Yang
(2001), Cheng & Yang (2003).
• Reading: G. Sun (forthcoming).
‘One clear conclusion is that there are many
important areas of economics in which the
recognition of increasing returns makes a big
difference, and changes the established wisdom
significantly. …we have not yet reached the
point of diminishing returns in the study of
increasing returns: there is a long way to go,
and the results of the work yet to be completed
will be interesting’ (Geoffrey Heal, 1999).
Different Types of IR
• IR at the firm level, economies of scale.
• IR at the industry level due to external
economies (Marshall 1920, Chipman 1970,
Romer 1986).
• IR at the economy level due to economies of
specialization (ES)/division of labour (DL)
(Smith, Young, Rosen, Yang, Buchanan).
• IR at the world level (Ethier 1979, Chandra
et al. 2002).
Different Analytical Sources of IR
• Property of the production function;
indivisibilities.
• External economies due to knowledge
transmission, economies internal to another
industry, etc.
• Higher productivity from the use of more
intermediate inputs (Ethier 1979, 1982).
• ES at the individual level (Smith, Yang).
Many Traditional Results Have to be
Drastically Revised
• Significant IR at the firm level is
inconsistent with perfect competition.
• Perfect competition also inconsistent
with the virtually omnipresent product
differentiation.
• But allowing for non-perfect
competition play havocs to many
traditional results.
A.Neutrality of money may not hold
• Even no time lags, money illusion, and other
frictions, just non-perfect competition may make a
change in nominal aggregate demand affect either
the price level (the monetarist case) or the real
output (the Keynesian case).
• Expectation wonderland (outcome depends on
expectation which will be self-fulfilling) and
cumulative expansion/contraction are also possible,
partly explaining some real-world phenomena like
business cycles, importance of confidence, and
difficulties of prediction (Ng 1977, 1980, 1986,
1992, 1998, 1999; Ng & Wu 2002).
In the non-traditional cases, there exists
an interfirm macroeconomic externality
where the expansion by each firm benefits
other firms apart from the familiar income
multiplier effects. This is an area where
welfare economics, macroeconomics and
its micro-foundation intersect, an area still
not adequately studied.
The crux of the difference
• Demand Side: A horizontal demand curve
cannot shift left or right, only up or down. But
an upward shift means an increase in price.
With no time lags, money illusion, this leads
to a similar shift in MC.
• Supply Side: MC upward-sloping under
perfect competition; may be horizontal or
downward sloping (esp. with IR) under nonperfect competition.
The analysis is based on a
representative firm but it takes account
of the influence of macro variables and
the interaction (including ‘infinite
number of feedback loops’) with the
rest of the economy, using a simplified
general-equilibrium method.
Moreover, a fully general-equilibrium
analysis is used to show
• (1) for any (exogenous) change in cost or demand,
there exists a hypothetical representative firm whose
response accurately represents that of the whole
economy in aggregate output and average price;
• (2) a representative firm defined by a simple
weighted average can be used as a good
approximation of the whole economy to any
economy-wide change in demand and/or costs that
does not result in drastic inter-firm changes. (See Ng
1986, App. 3I.)
B. Pecuniary external effects may
have real efficiency implications
• Even where the supply/demand
analysis is still applicable, if the supply
curve is downward sloping due to
whatever source of IR, the traditional
analysis showing the absence of
inefficiency of pecuniary ext. effects is
no longer valid.
C. Market equilibrium no longer
Pareto Optimal
• Well-known that IR may give rise to efficiency
problems (e.g. Arrow 1987, 2000, Guesnerie 1975,
Heal 1999, Quinzii 1992, Villar 1996).
• Pigou (1920) advocated tax/subsidy on goods with
up/downward sloping supply curves. Further
discussion (reprinted in AEA 1952) revealed
problems. Pigou’s example: a non-congested, wide
but uneven road and a congested, narrow but good
road, to illustrate the over-use of the narrow road
with increasing costs. Knight (1924): failure of
pricing the congested road. With optimal pricing, no
overuse.
• Dixit & Stiglitz’ (1977) show that no
general conclusion can be made.
• The more specific models of Heal (1980,
1999) show that the combination of
imperfection competition and IR leads to
the over-serving of large markets and
under-serving of small markets.
• See also Spence 1976 on optimal product
variety.
• Even abstracting from monopolistic output
restriction by assuming AC-pricing from
contestability, Section 2 shows that goods with
higher degrees of IR are under-expanded.
• Subsidies on goods with (high degrees of) IR
financed by taxes on goods with non and lower IR
may increase efficiency.
• But may open up a flood-gate of rent-seeking
activities. Perhaps it is optimal to continue to
pretend that IR do not exist. Ha!
• Unlikely true for all issues; otherwise, policies like
encouraging the development of the great western
region in China does not make sense.
Existence of AC-Pricing
Equilibria with IR
• Theorem 1 (Brown-Heal generalized): A
productively efficient AC-pricing equilibrium
exists.
• Proof: While the production possibility set need
not be convex, the production possibility frontier
(super-surface) is topologically equivalent to a
compact and convex set. From Brouwer’s fixed
point theorem, any continuous mapping of a set
homeomorphic to a compact and convex set onto
itself possess a fixed point. Thus, any continuous
mapping of the PPF has a fixed point.
• Consider the following continuous mapping Ф of
PPF into PPF: (G1, …, Gg)0 → (W1/WR, …, WR0 ; (P , …, P )0 → (Gd , …, Gd )1 → (G , …,
/W
)
1
R
1
G
1
g
1
Gg)2, where
• (i) (G1, …, Gg)0 is an arbitrary point on the PPF.
• (ii) (W1/WR, …, WR-1/WR)0 is the set of relative
resource prices determined by the common (to all
firms using the same pair of resources) marginal
rates of technical substitution as specified in (2.7)
above at the point Gg(R1g, …, RRg) = G0g; g = 1, …,
G, i.e. the same point as (G1, …, Gg)0.
• (iii) (P1, …, PG)0 = product prices at AC, i.e. P0g =
Cg(W1, …, WR, Gg)/Gg; g = 1, …, G, at the given
production levels given by (G1, …, Gg)0.
• (iv) (Gd1, …, Gdg)1 is the market demand for the
various goods, i.e. Gdg = G1g + …, GIg; g = 1, …, G,
where each Gig is the individual utility-maximization
quantity of the g good demanded by individual i at the
set of product prices (P1, …, PG)0 and resource prices
(W1/WR, …, WR-1/WR)0.
• (v) (G1, …, Gg)2 is the intersection of the ray through
the point (Gd1, …, Gdg)1 and the PPF.
• Since the mapping Ф is continuous and the PPF is
homeopmorphic to a compact and convex set, the
mapping has a fixed point which is denoted as (G1, …,
Gg)*. At this fixed point, (G1, …, Gg)0 = (Gd1, …, Gdg)1
= (G1, …, Gg)2 = (G1, …, Gg)*. Hence, demand for goods
(G1, …, Gg)1 equals supply (G1, …, Gg)0 at the product
prices (P1, …, PG)*, the AC of producing the various
goods at (G1, …, Gg)0. The equilibrium relative resource
prices (W1/WR, …, WR-1/WR)* is the common MRTS
specified in (2.7). This production point gives equilibrium
values of resource demand Rrg; r = 1, …, R; g = 1, …, G
satisfying (2.11). Finally, the individual demands for
products Gig; i = 1, …, I; g = 1, …, G total to satisfy
(2.10). Since the production point is on the PPF, it is
productively efficient. This completes the proof.
Efficiency of Encouraging Goods with
High Degrees of IR
•
•
•
•
•
•
•
•
•
(3.1)
Pg = Ag for all good g,
Define the (local) degree of IR
(3.2)
Ig - (Ag/Gg)Gg/Ag
(3.5)
Uig/Uih = Pg/Ph (Utility max.)
Pareto optimality: Uig/Uih = Fg/Fh = Mg/Mh
From (3.1) and (3.5), a market equilibrium:
(3.8)
Uig/Uih = Ag/Ah
(3.9)
Ig - (Ag/Gg)Gg/Ag = 1 – Mg/Ag
(3.10) Ig > Ih iff Ag/Ah > Mg/Mh.
• From (3.8) and (3.10): For any market equilibrium P:
(3.11)
MRSgh > Mg/Mh iff Ig > Ih.
• The (absolute) slope of PPF in the g/h plane equals Mg/Mh
(with good g on the horizontal axis).
• If good g has a higher degree of IR than good h, the
market-equilibrium MRSgh > slope of PPF.
• A movement down the (downward-sloping) PPF involving
more good g and less good h must reach a higher
indifference curve/surface.
• Theorem 2A: At an AC-pricing market equilibrium, if
the degree of IR for good g is larger than that for good
h, a point of higher efficiency (Pareto-superior) could
be reached by increasing good g and decreasing h.
• Next, a cost-benefit analysis is used to show
• Theorem 2B: At an AC-pricing market
equilibrium, if the production/consumption of
a good with a lower IR is decreased to allow for
a
corresponding
increase
in
the
production/consumption of another good with
a
higher
IR,
holding
the
consumption/production of other goods
unchanged, the aggregate net benefits of the
change is positive.
• A specific example confirms the above results.
• But, Information; rent-seeking.
Joint paper with D.S. Zhang
• The analysis of economies of specialization at the individual
level by Yang & Shi (1992) and Yang & Ng (1993) is
combined with the Dixit & Stiglitz (1977) analysis of
monopolistic-competitive firms to show that, even if both
the home and the market sectors have IR and there are no
pre-existing taxes, it is still efficient to tax the home sector
to finance a subsidy on the market sector to offset the underproduction of the latter due to the failure of price-taking
consumers to take account of the effects of higher
consumption in reducing the average costs and hence prices,
through IR or the publicness nature of fixed costs.
• But offset by environmental concerns.
Average-cost pricing,
increasing returns, and optimal
output in a model with home
and market production
Yew-Kwang Ng
Dept. of Economics, Monash University
Dingsheng Zhang
Dept. of Economics, Monash University
Institute for Advanced Economic Studies,
Wuhan University
The Model
Consider an economy with M identical
consumers. Each of them has the following
decision problem for consumption, working,
and home production.
Max:
1
u l
s.t.
[
rR
xr 1 ] 1 [
jJ
xj 2 ]
pr xr w(1 l l j )
rR
jJ
lj a
xj
c
2
The above optimization problem
gives the following solutions:
a
lh
1 2
2 (1 )
l
2 (1 2 )
(1 2 )
m
a[ 2 (1 2 )]
xr
2
1
1 1
1
1 1
[ 2 (1 2 )] pr ( s1 ps )
n
We assume that the market structure is
monopolistic competition. The production
function of good r is:
X r (lr A) / b
The first-order condition for the monopolist
to maximize profit with respect to output
level or price implies that
The general equilibrium values of
the various variables are :
1 A(n 1)
b(n 1 )
X
p
bn(1 1 )
1 (n 1)
1 A(n 1)
A(n 1 )
x
lr
bn(1 1 ) M
n(1 1 )
2 (1 )
a
l
lh
2 (1 2 )
1 2
(1 2 )
M 2 (1 1 )
n
1 m
a[ 2 (1 2 )]
A[ 2 (1 2 )]
Comparative statics analysis:
n
2 (1 1 )
0,
M A[ 2 (1 2 )]
n
M 2 (1 1 )
2
0,
A
A [ 2 (1 2 )]
n
M 2 (1 1 )
0,
A[ 2 (1 2 )]
n
M 2 (1 1 )(1 2 )
0,
2
A[ 2 (1 2 )]
n
M 2
1
0
1
A[ 2 (1 2 )]
m
2 (1 2 )
0,
2
a[ 2 (1 2 )]
m
(1 2 )
2
0,
a
a [ 2 (1 2 )]
m
0,
2
2 a[ 2 (1 2 )]
Equilibrium utility value:
1
2
ue l1 n x m xh
2
21 1 b M a
2
c A
1
(1 2 )
(1 )(1 ) [ 2 (1 2 )]
2
1
1
2
[ M 2 A( 2 (1 2 ))] {M 2 (1 1 ) A1[ 2 (1 2 )]}
1
To analyse the welfare properties,
we introduce the government to the
model
Assume that the tax rate of per unit home
labor is , and then consumer’s problem is
max u l
S.t.
1
[ xr ] [ x j ]
1
rR
2
1
2
jJ
pr xr l j w(1 l l j )
rR
jJ
jJ
lj a
xj
c
In addition, denoting the subsidy rate per
unit of market product as , the zeroprofit condition for each firm is
pr X r (b ) X r A
Government’s budget constrain is
Mm lh n X
we can get the equilibrium level of
utility as
1
2
ue l1 n x m xh
2
21 1 (b ) ( 1)
2
2
M
a
1
c A
(1 2 )
2
1
1
2
(1 )(1 ) [ 2 (1 2 )]
[ M 2 A( 2 (1 2 ))] {M 2 (1 1 ) A1[ 2 (1 2 )]}
B(b ) ( 1)
2
1
where
2
B 21 1 M a
[ 2 (1 2 )]
2
c A
1
(1 2 )
2
(1 )(1 )
1
1
2
[ M 2 A( 2 (1 2 ))]
{M 2 (1 1 ) A1[ 2 (1 2 )]}
1
The effect of a change in tax rate on the
equilibrium value of utility with respect to
the tax rate, and with the subsidy rate at
whatever level that is allowed by the
government budget constraint as varies,
evaluated at 0 , is given by
Bb [ M 2 (1 1 ) A1 ( 2 (1 2 )]
due
0
d 0
12[ M 2 A( 2 (1 2 ))]
This means that, starting from the original position
without any tax/subsidy, a tax on home production
which finances for a subsidy on market production
increases utility, ignoring administrative costs and
any possible side effects, such as rent-seeking
activities triggered by the subsidy. Since all firms
just break-even in equilibrium, we may base our
welfare comparisons simply on the utility levels
alone. We thus have,
Proposition 1: In our model with both home
and market production under the conditions
of increasing returns and average-cost
pricing, a subsidy, if not excessive, on
market production financed by a tax on home
production improves efficiency even if the
initial position involves no tax distortion,
ignoring administrative costs and any
possible side effects.
We extend the above model to allow for
different sectors of market goods that may
have different degrees of elasticity of
substitution and different degrees of
increasing returns (through different
values of the fixed cost and marginal cost),
we have similar results.
Proposition 2: In our model with both home
and market production under the conditions
of increasing returns and average-cost
pricing with two sectors of different fixed
costs, elasticities of substitution, and degree
of importance in preference, it is efficient to
tax the sector with lower fixed costs, higher
elasticity of substitution and/or higher
degree of importance in preference and
subsidize the other.
Concluding Remarks
Our conclusions’ applicability to the real
economy is subject to important
qualifications. First, the government may
not have the information to differentiate
which goods should be taxed (and by how
much) and which subsidized. Secondly,
we have not considered other factors
(including rent seeking) causing imperfect
efficiency in the real economy.