Download Mankiw 5/e Chapter 8: Economic Growth II

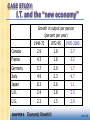
macro
CHAPTER EIGHT
Economic Growth II
macroeconomics
fifth edition
N. Gregory Mankiw
PowerPoint® Slides
prepared by Ming-Jang Weng
© 2002 Worth Publishers, all rights reserved
Chapter 8 Learning objectives
 Technological progress in the Solow model
 Policies to promote growth
 Growth empirics:
Confronting the theory with facts
 Endogenous growth:
Two simple models in which the rate of
technological progress is endogenous
CHAPTER 8
Economic Growth II
slide 1
Introduction
In the Solow model of Chapter 7,
 the production technology is held constant
 income per capita is constant in the steady
state.
Neither point is true in the real world:
 1929-2001: U.S. real GDP per person grew
by a factor of 4.8, or 2.2% per year.
 examples of technological progress abound
(see next slide)
CHAPTER 8
Economic Growth II
slide 2
Examples of technological progress
 1970: 50,000 computers in the world
2000: 51% of U.S. households have 1 or more computers
 The real price of computer power has fallen an average of
30% per year over the past three decades.
 The average car built in 1996 contained more computer
processing power than the first lunar landing craft in 1969.
 Modems are 22 times faster today than two decades ago.
 Since 1980, semiconductor usage per unit of GDP has
increased by a factor of 3500.
 1981: 213 computers connected to the Internet
2000: 60 million computers connected to the Internet
CHAPTER 8
Economic Growth II
slide 3
Tech. progress in the Solow model
 A new variable: E = labor efficiency
 Assume:
Technological progress is labor-augmenting:
it increases labor efficiency at the exogenous
rate g:
g
CHAPTER 8
E
E
Economic Growth II
slide 4
Tech. progress in the Solow model
 We now write the production function as:
Y  F (K , L  E )
 where L  E = the number of effective
workers.
– Hence, increases in labor efficiency have
the same effect on output as increases in
the labor force.
CHAPTER 8
Economic Growth II
slide 5
Tech. progress in the Solow model
 Notation:
y = Y/LE = output per effective worker
k = K/LE = capital per effective worker
 Production function per effective worker:
y = f(k)
 Saving and investment per effective worker:
s y = s f(k)
CHAPTER 8
Economic Growth II
slide 6
Tech. progress in the Solow model
 Derivation of the equation of motion for K
 K ( net investment )  I ( gross investment )    K ( depreciation )

K
LE

I
LE
Since k   (
=

K
LE
K
LE

K
LE
) 
 i    k  s  f (k )    k
( L  E ) K  K ( L  E  E  L )
K
LE
( L  E )2
(
L
L

E
E
)
 s  f ( k )    k  k ( n  g ), where
L
L
 n , and
E
E
 g
 k  s  f ( k )  (  n  g ) k
CHAPTER 8
Economic Growth II
slide 7
Tech. progress in the Solow model
( + n + g)k = break-even investment:
the amount of investment necessary
to keep k constant.
Consists of:
 k to replace depreciating capital
n k to provide capital for new workers
g k to provide capital for the new
“effective” workers created by
technological progress
CHAPTER 8
Economic Growth II
slide 8
Tech. progress in the Solow model
Investment,
break-even
investment
k = s f(k)  ( +n +g)k
( +n +g ) k
sf(k)
k*
CHAPTER 8
Economic Growth II
Capital per
effective
worker, k
slide 9
Steady-State Growth Rates in the
Solow Model with Tech. Progress
symbol
Steady-state
growth rate
Capital per
effective worker
k = K/ (L E )
0
Output per
effective worker
y = Y/ (L E )
0
Capital per worker (K/ L ) = k E
g
Output per worker (Y/ L ) = y E
g
variable
Total output
CHAPTER 8
Y = y E L
Economic Growth II
n+g
slide 10
The Golden Rule
To find the Golden Rule capital stock,
express c* in terms of k*:
In the Golden
Rule Steady State,
c* = y*  i*
the marginal
= f (k* )  ( + n + g) k*
product of capital
c* is maximized when
net of depreciation
equals the
MPK =  + n + g
pop. growth rate
or equivalently,
plus the rate of
MPK   = n + g
tech progress.
CHAPTER 8
Economic Growth II
slide 11
Policies to promote growth
Four policy questions:
1. Are we saving enough? Too much?
2. What policies might change the saving rate?
3. How should we allocate our investment
between privately owned physical capital,
public infrastructure, and “human capital”?
4. What policies might encourage faster
technological progress?
CHAPTER 8
Economic Growth II
slide 12
Are we saving enough? Too much?
Investment,
break-even
investment
f(k *)
The saving rate,
s’, is too high to
reach the golden
rule consumption.
s’f(k*)
c
k
CHAPTER 8
*
gold
*
gold
Economic Growth II
s*f(k*)
Capital per
effective worker,
k
slide 13
1. Evaluating the Rate of Saving
 Use the Golden Rule to determine whether
our saving rate and capital stock are too high,
too low, or about right.
 To do this, we need to compare
(MPK   ) to (n + g ).
 If (MPK   ) > (n + g ), then we are below the
Golden Rule steady state and should increase s.
 If (MPK   ) < (n + g ), then we are above the
Golden Rule steady state and should reduce s.
CHAPTER 8
Economic Growth II
slide 14
1. Evaluating the Rate of Saving
To estimate (MPK   ), we use
three facts about the U.S. economy:
1. k = 2.5 y
The capital stock is about 2.5 times one
year’s GDP.
2.  k = 0.1 y
About 10% of GDP is used to replace
depreciating capital.
3. MPK  k = 0.3 y
Capital income is about 30% of GDP
CHAPTER 8
Economic Growth II
slide 15
1. Evaluating the Rate of Saving
1. k = 2.5 y
2.  k = 0.1 y
3. MPK  k = 0.3 y
To determine  , divided 2 by 1:
k
0.1 y

k
2.5 y
CHAPTER 8

0.1
 
 0.04
2.5
Economic Growth II
slide 16
1. Evaluating the Rate of Saving
1. k = 2.5 y
2.  k = 0.1 y
3. MPK  k = 0.3 y
To determine MPK, divided 3 by 1:
MPK  k
k
0.3 y

2.5 y

0.3
MPK 
 0.12
2.5
Hence, MPK   = 0.12  0.04 = 0.08
CHAPTER 8
Economic Growth II
slide 17
1. Evaluating the Rate of Saving
 From the last slide: MPK   = 0.08
 U.S. real GDP grows an average of 3%/year,
so n + g = 0.03
 Thus, in the U.S.,
MPK   = 0.08 > 0.03 = n + g
 Conclusion:
The U.S. is below the Golden Rule steady state:
if we increase our saving rate, we will have faster
growth until we get to a new steady state with
higher consumption per capita.
CHAPTER 8
Economic Growth II
slide 18
2. Policies to increase the saving rate
 Reduce the government budget deficit
(or increase the budget surplus)
 Increase incentives for private saving:
 reduce capital gains tax, corporate income
tax, estate tax as they discourage saving
 replace federal income tax with a
consumption tax
 expand tax incentives for IRAs (individual
retirement accounts) and other retirement
savings accounts
CHAPTER 8
Economic Growth II
slide 19
3. Allocating the economy’s investment
 In the Solow model, there’s one type of capital.
 In the real world, there are many types,
which we can divide into three categories:
– private capital stock
– public infrastructure
– human capital: the knowledge and skills
that workers acquire through education
 How should we allocate investment among
these types?
CHAPTER 8
Economic Growth II
slide 20
Allocating the economy’s investment:
two viewpoints
1. Equalize tax treatment of all types of capital
in all industries, then let the market allocate
investment to the type with the highest
marginal product.
2. Industrial policy: Gov’t should actively
encourage investment in capital of certain
types or in certain industries, because they
may have positive externalities (by-products)
that private investors don’t consider.
CHAPTER 8
Economic Growth II
slide 21
Possible problems with industrial policy
 Does the gov’t have the ability to “pick
winners” (choose industries with the highest
return to capital or biggest externalities)?
 Would politics (e.g. campaign contributions)
rather than economics influence which
industries get preferential treatment?
CHAPTER 8
Economic Growth II
slide 22
4. Encouraging technological progress
 Patent laws:
encourage innovation by granting temporary
monopolies to inventors of new products
 Tax incentives for R&D
 Grants to fund basic research at universities
 Industrial policy:
encourage specific industries that are key for
rapid tech. progress
(subject to the concerns on the preceding slide)
CHAPTER 8
Economic Growth II
slide 23
CASE STUDY:
The Productivity Slowdown
Growth in output per person
(percent per year)
1948-72
1972-95
Canada
2.9
1.8
France
4.3
1.6
Germany
5.7
2.0
Italy
4.9
2.3
Japan
8.2
2.6
U.K.
2.4
1.8
U.S.
2.2
1.5
CHAPTER 8
Economic Growth II
slide 24
Explanations?
 Measurement problems
Increases in productivity not fully measured.
– But: Why would measurement problems
be worse after 1972 than before?
 Oil prices
Oil shocks occurred about when productivity
slowdown began.
– But: Then why didn’t productivity speed up
when oil prices fell in the mid-1980s?
CHAPTER 8
Economic Growth II
slide 25
Explanations?
 Worker quality
1970s - large influx of new entrants into
labor force (baby boomers, women).
New workers are less productive than
experienced workers.
 The depletion of ideas
Perhaps the slow growth of 1972-1995 is
normal and the true anomaly was the rapid
growth from 1948-1972.
CHAPTER 8
Economic Growth II
slide 26
The bottom line:
We don’t know which of these
is the true explanation,
it’s probably a combination
of several of them.
CHAPTER 8
Economic Growth II
slide 27
CASE STUDY:
I.T. and the “new economy”
Growth in output per person
(percent per year)
1948-72
1972-95
1995-2000
Canada
2.9
1.8
2.7
France
4.3
1.6
2.2
Germany
5.7
2.0
1.7
Italy
4.9
2.3
4.7
Japan
8.2
2.6
1.1
U.K.
2.4
1.8
2.5
U.S.
2.2
1.5
2.9
CHAPTER 8
Economic Growth II
slide 28
CASE STUDY:
I.T. and the “new economy”
Apparently, the computer revolution didn’t affect
aggregate productivity until the mid-1990s.
Two reasons:
1. Computer industry’s share of GDP much
bigger in late 1990s than earlier.
2. Takes time for firms to determine how to
utilize new technology most effectively
The big questions:
 Will the growth spurt of the late 1990s continue?
 Will I.T. remain an engine of growth?
CHAPTER 8
Economic Growth II
slide 29
A Nobel Laureate’s Words
I do not see how one can look at figures like
these without seeing them as possibilities. Is
there some action a government of India
could take that would lead the Indian
economy to grow like Indonesia’s or
Egypt’s ? If so, what, exactly? If not, what is
it about the “nature of India” that makes it
so? The consequences for human welfare
involved in questions like these are simply
staggering: Once one starts to think about
them, it is hard to think about anything else.
Robert E. Lucas, Jr., “On the Mechanics of Economic Development,” Journal of
Monetary Economics, July 1988.
CHAPTER 8
Economic Growth II
slide 30
Growth empirics: Confronting the
Solow model with the facts
Solow model’s steady state exhibits
balanced growth - many variables grow
at the same rate.
 Solow model predicts Y/L and K/L grow at
same rate (g), so that K/Y should be constant.
This is true in the real world.
 Solow model predicts real wage grows at same
rate as Y/L, while real rental price is constant.
Also true in the real world.
CHAPTER 8
Economic Growth II
slide 31
Convergence
 Solow model predicts that, other things equal,
“poor” countries (with lower Y/L and K/L )
should grow faster than “rich” ones.
 If true, then the income gap between rich &
poor countries would shrink over time, and
living standards “converge.”
 In real world, many poor countries do NOT
grow faster than rich ones. Does this mean
the Solow model fails?
CHAPTER 8
Economic Growth II
slide 32
Convergence
 No, because “other things” aren’t equal.
 In samples of countries with similar savings
& pop. growth rates,
income gaps shrink about 2%/year.
 In larger samples, if one controls for differences
in saving, population growth, and human capital,
incomes converge by about 2%/year.
 What the Solow model really predicts is
conditional convergence - countries converge
to their own steady states, which are determined
by saving, population growth, and education.
And this prediction comes true in the real world.
CHAPTER 8
Economic Growth II
slide 33
Factor accumulation vs.
Production efficiency
Two reasons why income per capita are lower
in some countries than others:
1. Differences in capital (physical or human)
per worker
2. Differences in the efficiency of production
(the height of the production function)
Studies:
 both factors are important
 countries with higher capital (phys or human)
per worker also tend to have higher
production efficiency
CHAPTER 8
Economic Growth II
slide 34
GDP Per Capita
1990 Dollars
1950
United States
1992
Cumulative
Growth, %
9,573
21,558
125.20
Bangladesh
551
720
30.67
China
214
430
100.93
Egypt
517
1,927
272.73
India
597
1,348
125.80
Indonesia
874
2,749
214.53
2,085
5,112
145.18
South Korea
876
10,010
1,042.69
Taiwan
922
11,590
1,157.05
Tanzania
427
604
41.45
Thailand
848
4,694
453.54
2,834
4,671
64.82
636
407
-36.01
Mexico
U.S.S.R.
Zaire
Source: Angus Maddison, Monitoring the World Economy 1820-1992 (Paris: Organization for Economic Cooperation and Development, 1995)
CHAPTER 8
Economic Growth II
slide 36
Endogenous Growth Theory
 Solow model:
– sustained growth in living standards is due
to tech progress
– the rate of technological progress is
exogenous
 Endogenous growth theory:
– a set of models in which the growth rate of
productivity and living standards is
endogenous
CHAPTER 8
Economic Growth II
slide 37
A basic model
 Production function: Y = A K
where A is the amount of output for each
unit of capital (A is exogenous & constant)
 Key difference between this model & Solow:
MPK is constant here, diminishes in Solow
 Investment: s Y
 Depreciation:  K
 Equation of motion for total capital:
K = s Y   K
CHAPTER 8
Economic Growth II
slide 38
A basic model
K = s Y   K
 Divide through by K and use Y = A K , get:
Y
K

 sA  
Y
K
 If s A > , then income will grow forever,
and investment is the “engine of growth.”
 Here, the permanent growth rate depends
on s. In Solow model, it does not.
CHAPTER 8
Economic Growth II
slide 39
Does capital have diminishing returns
or not?
 Yes, if “capital” is narrowly defined (plant
& equipment).
 Perhaps not, with a broad definition of
“capital” (physical & human capital,
knowledge).
 Some economists believe that knowledge
exhibits increasing returns.
CHAPTER 8
Economic Growth II
slide 40
A two-sector model
 Two sectors:
– manufacturing firms produce goods
– research universities produce knowledge that
increases labor efficiency in manufacturing
 u = fraction of labor in research
(u is exogenous)
 Mfg prod func: Y = F [K, (1-u )E L]
 Research prod func: E = g (u )E
 Capital accumulation: K = s Y   K
CHAPTER 8
Economic Growth II
slide 41
A two-sector model
 In the steady state, mfg output per worker
and the standard of living grow at rate
E/E = g (u ).
 Key variables:
s: affects the level of income, but not its
growth rate (same as in Solow model)
u: affects level and growth rate of income
 Question:
Would an increase in u be unambiguously
good for the economy?
CHAPTER 8
Economic Growth II
slide 42
Three facts about R&D in the real world
1. Much research is done by firms seeking profits.
2. Firms profit from research because
• new inventions can be patented, creating a stream
of monopoly profits until the patent expires
• there is an advantage to being the first firm on
the market with a new product
3. Innovation produces externalities that reduce
the cost of subsequent innovation.
Much of the new endogenous growth theory
attempts to incorporate these facts into models
to better understand technological progress.
CHAPTER 8
Economic Growth II
slide 43
Is the private sector doing enough R&D?
 The existence of positive externalities in the
creation of knowledge suggests that the private
sector is not doing enough R&D.
 But, there is much duplication of R&D effort
among competing firms.
 Estimates: The social return to R&D is at least
40% per year.
Thus, many believe government should encourage
R&D.
CHAPTER 8
Economic Growth II
slide 44
Accounting for the Sources of
Economic Growth
 Production Function (CRTS)
Y  F ( K , L)
 Increases in Capital and Labor
Y  ( MPK  K )  ( MPL  L)
F
G
H
F
H
IJ
K
IK
F
G
H
F
H
IJ
K
IK
Y
MPK  K K
MPL  L L



Y
Y
K
Y
L
Y
Capital' s share K
Labor' s share L


 of output
of
output
Y
K
L
Y
K
L


 (1   )
Y
K
L
where  is capital' s share and (1   ) is labor' s share.
CHAPTER 8
Economic Growth II
slide 45
Accounting for the Sources of
Economic Growth
 Production Function with Technology
Y  AF ( K , L)
 Technological Progress
Y
Y
Growth in
output
K
L
 
 (1   )

K
L

Contribution
Contribution

of capital
of labor

A
A
Growth in Total
Factor Productivity
The above is the growth-accounting equation.
CHAPTER 8
Economic Growth II
slide 46
Accounting for the Sources of
Economic Growth
 Solow Residual
A Y
K
L


 (1   )
A
Y
K
L
 ΔA/A is the change in output that cannot be explained
by changes in inputs. Thus, the growth in total factor
productivity is computed as a residual – that is, as the
amount of output growth that remains after we have
accounted for the determinants of growth that we can
measure. Indeed, ΔA/A is sometimes called the
Solow residual, after Robert Solow, who first showed
how to compute it.
CHAPTER 8
Economic Growth II
slide 47
Accounting for Economic Growth in
the United States
SOURCE OF GROWTH
(average
percentage, %,
Labor
   Total Factor Productivity 
increase per year)  Output Grow th   Capital   

 Y / Y   K / K   (1   )L / L  
A / A



Years
1950-1960
3.5
1.1
0.8
1.6
1960-1970
4.1
1.2
1.3
1.7
1970-1980
3.1
0.9
1.6
0.5
1980-1990
2.9
0.8
1.3
0.8
1990-1996
2.2
0.6
0.8
0.8
1950-1996
3.2
0.9
1.2
1.1
Source: U.S. Department of Commerce, U.S. Department of Labor, and the author’s
Calculations. The parameter α is set to equal 0.3.
CHAPTER 8
Economic Growth II
slide 48
Growth in the Asian Tigers
Hong Kong
Singapore
South Korea
Taiwan
(1966-1991)
(1966-1990)
(1966-1990)
(1966-1990)
GDP per
capita growth
5.7
6.8
6.8
6.7
TFP* growth
2.3
0.2
1.7
2.6
Δ% labor
force
participation
38→49
27→51
27→36
28→37
26.5→75.0
25.8→67.6
%
Δ% secondary
education or
27.2→71.4 15.8→66.3
higher
*TFP: total factor productivity
Source: Alwyn Young, “The Tyranny of Numbers: Confronting the Statistical Realities of
the East Asian Growth Experience,” Quarterly Journal of Economics, August 1995.
CHAPTER 8
Economic Growth II
slide 49
Chapter summary
1. Key results from Solow model with tech
progress
 steady state growth rate of income per
person depends solely on the exogenous rate
of tech progress
 the U.S. has much less capital than the
Golden Rule steady state
2. Ways to increase the saving rate
 increase public saving (reduce budget deficit)
 tax incentives for private saving
CHAPTER 8
Economic Growth II
slide 50
Chapter summary
3. Productivity slowdown & “new economy”
 Early 1970s: productivity growth fell in the
U.S. and other countries.
 Mid 1990s: productivity growth increased,
probably because of advances in I.T.
4. Empirical studies
 Solow model explains balanced growth,
conditional convergence
 Cross-country variation in living standards
due to differences in cap. accumulation and
in production efficiency
CHAPTER 8
Economic Growth II
slide 51
Chapter summary
5. Endogenous growth theory: models that
 examine the determinants of the rate of
tech progress, which Solow takes as given
 explain decisions that determine the creation
of knowledge through R&D
CHAPTER 8
Economic Growth II
slide 52
Thanks for your attention!!
Dr. Weng
CHAPTER 8
Economic Growth II
slide 53