Download Adders


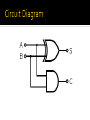
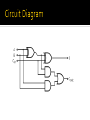
Arithmetic circuit
 Addition
 Subtraction
 Division
 Multiplication




0+0=0
0+1=1
1+0=1
1 + 1 = 10
One bit in sum
Two bit in sum

A combinational circuit that performs the
addition of two bits.

Two inputs and two outputs.

Augend and Addend

Sum and Carry
X
Y
C
S
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0

A combinational circuit that performs the
addition of three input bits.

Three inputs and two outputs.

Sum and Carry
X
Y
Z
C
S
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
0
0
1
0
1
1
1
0
1
1
0
1
0
0
1


Adders connected in cascade.
Carry output from one full adder connected
to carry input of next full adder.





Input carry
A
B
Sum
Output carry
0110
1011
0011
1110
0011

Input carry in the least significant position is
0.

Simple in concept.
Long circuit delay.

 Many gates in the carry path.

Practical design with reduced delay.

For a n- bit ripple carry adder
 The longest delay path is 2n + 2.
 16 – bit ripple carry adder - delay is 34 gate delays

Designed by a transformation of the ripple
carry adder design in which the carry logic
over fixed groups of bits of the adder is
reduced to two-level logic.

OR gate and one of the AND gates are
removed to form each of the full adders to
form the ripple carry adder.

Separate the parts of full adders not involving
the carry propagation path from those
containing the path.

First part of each full adder
 partial full adder - PFA

Two outputs
 Pi and Gi
 From each PFA to ripple carry path

One input
 Ci
 From the carry path to each PFA


Pi = Ai XOR Bi - Propagate function
Gi = Ai . Bi - Generate function

Whenever Pi = 1
 Incoming carry is propagated through bit position
from Ci+1.

Whenever Pi = 0
 carry propagation through bit position is blocked.

Whenever Gi = 1
 Carry output from the position is 1.
 Regardless of value of Pi.
 A Carry has been generated.

Whenever Gi = 0
 carry is not generated.
 Ci+1 is 0.
 Ci is also 0.



Generate and propagate functions correspond
exactly to the half adder.
Essential in controling the values in ripple
carry path.
PFA generates sum function by XOR of
incoming carry, Ci and propagate function, Pi.