Download PowerPoint 演示文稿

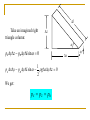
Chapter 15 FLUIDS
15.1 Fluid and the World Around Us
1. A fluid is a substance that cannot support a shearing stress.
2. Both gases and liquids are fluids.
3. Fluids in some cases can be regarded as incompressible and
no viscosity. These kinds of fluids are regarded as ideal
fluids.
15.2 Pressure  Depth Relation
Hydrostatics: Fluid statics is concerned with fluids in which the
center of mass of each fluid particle has zero velocity and
zero acceleration.
A fluid that is at rest is said to be in hydrostatic equilibrium.
The internal stress is normal and compressive. It is called
pressure:
F
p  lim
S  0 S
The unit of pressure is also pascal in SI.
1 atm = 760 mmHg = 1.013  104 N/m2
l
Take an imagined right
triangle column:
z

pxyz  pnyl sin  0
1
pz xy  pn yl sin   gxyz  0
2
We get:
px  pz  pn
x
y
The pressure in equal-heights
p A S  p B S
S
It gives out:
A
B
p A  pB
Then, the pressures at the same depth of a static fluid is equal in
magnitude.
The relationship between pressure and depth:
S
z
( p  dp) A  gAdy  pA  0
p2
y2
1
1
p dp  y
gdy
p 2  p1   g ( y 2  y1 )
The equal-pressure surface consists of equal height positions.
A volume force is the force exerted on each volume element:
f i  mi g
It is found that gravity is perpendicular to the equal-pressure
surface.
DEDUCTION:
Volume force is always perpendicular to the equal-pressure
surfaces.
Archimedes’ Principle:
When a body is fully or partially submerged in a fluid, a
buoyant force from surrounding fluid acts on the body. The force
is directed upward and has a magnitude equal to the weight of
the fluid that has been displaced by the force.
Pascal’s Principle:
A change in the pressure applied to an incompressible fluid is
transmitted undiminished to every portion of the fluid and to the
walls of its container.
15.3 Fluid Dynamics
15.3.1 Ideal fluids in motion
Euler’s method:
   f ( x, y , z , t )

 v  g ( x, y , z , t )
Therefore, the concepts of stream line and flow tube are used to
describe the fluids in motion.
Steady flows:
Ideal fluids:
1. Incompressible flow
2. Nonviscous flow
15.3.2 The equation of continuity
A2
Mass into segment:
m1  A1u1t
Mass out segment:
A1

v1
m2  A2u2t
We get
A1u1  A2u2
This is called the equation of continuity for steady and
impressible flow.

v2
15.3.3 Bernoulli’s Equation
l2
l1
p1
p2
The work done by the pressure force p1A1 is p1A1l1;
The work done by the pressure force p2A2 is p2A2l2;
The work done by gravity is mg(y2  y1).
Therefore, the work done by the resultant force is
W  p1 A1 l1  p 2 A2 l 2  mg ( y 2  y1 )
The change in kinetic energy is
1
1
2
E k  mv 2  mv12
2
2
We get
1
1
2
p1 A1 l1  p 2 A2 l 2  mg ( y 2  y1 )  mv 2  mv12
2
2
We rearrange it to read
1 2
p  v  gy  constant
2
This is called Bernoulli’s equation for steady, nonviscous,
incompressible flows only.
There are many applications associated with this equation.
15.4 Viscosity
In fluids, the analog of the shear modulus for solids is the
ratio of the shear stress to the rate of strain. This ratio is termed
the dynamic viscosity

shear stress
F/A

rate of shear strain du / dy
du
F 
A
dy
That is to say, internal friction (viscous force) is proportional to
velocity gradient and the area of contact layer.
15.5 Turbulence
Laminar flow is a stable streamline flow in a viscous fluid of
which flow speed is small.
A random and irregular motion of the fluid is referred to as
turbulent flow.
Reynolds number:
uL
R

Where L is some characteristic length associated with the flow.
When a flow becomes unstable and turbulent, the value of the
Reynolds number is called the critical Reynolds number.
R  RC
Poiseuille equation for horizontal and pipe-like laminar flows:
Velocity:
p1  p 2
v
(R 2  r 2 )
4L
Volume flux:
R 4
Q
( p1  p 2 )
8L
v(r)
p1
p2
L
Problems:
1.
2.
3.
4.
5.
6.
15-7 (on page 341),
15-18,
15-19,
15-40,
15-46,
15-57.