* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Universal Gravitation Chapter 12
Theoretical astronomy wikipedia , lookup
Copernican heliocentrism wikipedia , lookup
Astrobiology wikipedia , lookup
Formation and evolution of the Solar System wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Lunar theory wikipedia , lookup
Equivalence principle wikipedia , lookup
Rare Earth hypothesis wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Extraterrestrial life wikipedia , lookup
Comparative planetary science wikipedia , lookup
Geocentric model wikipedia , lookup
Satellite system (astronomy) wikipedia , lookup
Astronomical unit wikipedia , lookup
Dialogue Concerning the Two Chief World Systems wikipedia , lookup
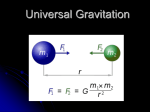
Universal Gravitation Chapter 12 Johannes Kepler Johannes Kepler was a German mathematician, astronomer and astrologer, and key figure in the 17th century Scientific revolution. He is best known for his laws of planetary motion, During his career, Kepler was a mathematics teacher at a seminary school in Graz, Austria, an assistant to astronomer Tycho Brahe, He also did fundamental work in the field of optics, invented an improved version of the refracting telescope (the Keplerian Telescope), and helped to legitimize the telescopic discoveries of his contemporary Galileo Galilei. Geocentric Model A model of the solar system which holds that the earth is at the centre of the universe and all other bodies are in orbit around it. Heliocentric Model Theory of the universe that states the sun is the centre, and that the earth revolves around it. Other Models There where also a wide variety of other different models that tried to explain the motion of the planets. Many of these where very complicated and hard to understand. Kepler's Three “LAWS” Kepler's laws of planetary motion are three mathematical laws that describe the motion of planets in the Solar System Kepler’s First Law The path of the planets about the sun are elliptical in shape, with the centre of the sun being located at one focus. Kepler’s Second Law An Imaginary line drawn from the centre of the sun to the centre of the planet will sweep out equal areas in equal intervals of time. Kepler’s Second Law Kepler’s Third Law The ratio of the squares of the periods of any two plants revolving about the sun is equal to the ratio of the cubes of their average distances from the sun. Thus, if Ta and Tb are their periods and ra and rb are their average distances from the sun, then we get a following equation. 2 Ta ra Tb rb 3 Astronomical Units (AU) An AU is a unit of distance that is defined as the average distance between the Sun and Earth. Example problem: (Using Keplers third law to find an orbital period) Galileo discovered four moons of Jupiter. Io, which he measured to be 4.2 units from the center of Jupiter, has a period of 1.8 days. He measured the radius of Ganymede’s orbit to be 10.7 units. Use Kepler’s third law to find the period of Ganymede. Ta ? Tb 1.8days ra 10.7units rb 4.2units 2 Ta ra Tb rb 3 ra T Tb rb 2 a 2 10.7units Ta2 1.8days 4.2 units 2 3 Ta 7.3days 3 Example problem (Using Keplers third law to find an orbital radius) The fourth moon of Jupiter, Callisto, has a period of 16.7 days. Find its distance from Jupiter using the same units as Galileo used. Ra=18.5 units Example problem Copernicus found the period of Saturn to be 29.5 earth years and it’s orbital radius to be 9.2 AU. Use these measurements and units to predict the orbital radius of Mars, whose period is 687 days. rb=1.47 AU Practice Problems (1-4) Reviewing Concepts (1 & 3) Applying Concepts (1) Problems (1-5) Newton's Law of Universal Gravitation The force of gravity is proportional to the product of the two masses that are interacting and inversely proportional to the square of the distance between their centres m1m2 Fg G 2 r Where: F G m1 m2 r is the Gravitational Force is the Gravitational Constant (6.67 × 10−-11 N m2 /kg2) is the mass of first object is the mass of second object is the distance between the objects Example problem Determine the force of gravitational attraction between the earth (m = 5.98 x 1024 kg) and a 70-kg physics student if the student is standing at sea level, a distance of 6.37 x 106 m from earth's centre. F= 688 N Example problem A 65.0 kg astronaut is walking on the surface of the moon, which has a mean radius of 1.74x103 km and a mass of 7.35x1022 kg. What is the weight of the astronaut? 105 N Example problem Now let’s use Newton’s law of universal gravitation to calculate the force of gravity here on Earth. m1m2 Fg G 2 r 24 5.98 10 m2 11 Fg 6.67 10 (6.37 106 )2 Fg 9.8m2 As you can see Newton’s law of universal gravitation is really another version of his second law of motion F=ma Pg 580 #’s 1 - 8 Gravitational Fields So far we have studied gravitational interaction in two related manners. First, we studied it in terms of energy AKA. gravitational potential Energy Then in terms of force. AKA Weight Yet there is another way to look at gravitational interactions. We can study it in terms of what is called a gravitational field. In the simplest form, we define a gravitational field as a region in which gravitational force can be experienced. For example here on earth at sea level we can experience the force of gravity. More specifically we are said to be within a gravitational field with a field intensity of 9.8 m/s2 What we have traditionally referred to as, the value of g (g = 9.8 m/s2), is a specific case example of the strength of the gravitational field intensity here on earth at sea level. Gravitational field intensity will change in strength as the separation between the two mass changes We have already seen this in the case where the value of g is larger at the bottom of a trench, and smaller on top of a mountain The following is a diagram of the gravitational field intensity of both the earth and moon system. Can be seen that both the magnitude and direction of the value g changes with location. We can also see gravitational field intensity by looking at Newton’s law of universal gravitation m1m2 Fg G 2 r If we now substitute in the values for Earth at sea level we get 24 5.98 10 m2 11 Fg 6.67 10 (6.37 106 )2 Now simplified to get Fg 9.8m2 We can now see that the gravitational field intensity (g) can be found by the manner m1m2 Fg G 2 r 24 5.98 10 m2 11 Fg 6.67 10 (6.37 106 )2 Fg 9.8m2 From this it can be seen that the universal formula for gradational field intensity is m1 g G 2 r Or equivalently, if the gravitational force (weight) is known and radius is not. g Fg m2 Example problem A mass of 4.60 kg is placed 6.37x106 m from the center of a planet and experiences a gravitational force of attraction of 45.1 N. Calculate the gravitational field intensity at this location. 9.8 m/s2 Example problem An astronaut is sitting on the seat of a 1100.0 kg lunar rover, on the surface of the Moon. The seat is 50.0 cm above the centre of mass of the rover. What gravitational field intensity does the rover exert on the astronaut? 2.93 107 N/kg [down] Do #’s 15 – 19 pg 649 Tying universal gravitation to circular motion Since the planets are not flying off into space (ie in a straight line) there must be a force causing them to stay in orbit, which would have to be some sort of centripetal force . Fc mpv r 2 Here the gravitational force of the sun can be thought of as that centripetal force which is causing the circular motion. Fg G ms m p r 2 So if the gravitational force is the centripetal force, we can equate them to get G ms m p r 2 mpv 2 r ms 2 G v r which gives us a formula for calculating orbital velocity ms v G r We also know that for circular motion 2r v T Therefor by substituting this in for the velocity we get ms 2 r G r T 2 3 Then rearrange to get Gms r 2 2 T 4 Where ms is the mass of the planet or star which the object is orbiting around Example problem How fast is the moon moving as it orbits Earth at a distance of 3.84 x 105 km from earth’s centre? ms v G r 1.02x103 m/s Example problem A satellite in low Earth orbit is 225 km above the surface. What is it’s orbital velocity? 7.78 km/s Practice Problems (5-8) Reviewing Concepts (4-9) Applying Concepts (2-11) Problems (6-19) Weightlessness Fact or Myth? To help answer this lets examine the fallowing scenario. If a space station has an orbit of 226 km, and an astronaut has a mass of 65 kg use Newton's law of gravitation to find their weight Fg G ms m p r 2 In actual fact there is no such thing as weightlessness, NASA coined the phase “micro gravity” to describe the condition of “apparent weightlessness”. This is the feeling an object would experience during free fall and is caused by simply not having a normal force to counteract the force of gravity. Simply put a person can be “weightless” right here on Earth simply by removing their normal force. AKA. If they are in free fall. Question? What keeps a satellite up in orbit? What prevents it from falling out of the sky? Answer: Nothing! It is falling! It just keeps missing the earth. What is a satellite? An object that revolves around a planet in a circular or elliptical path is termed a satellite. The moon is Earth's original satellite but there are many manmade satellites, mostly closer to Earth. The path that a satellite follows is termed an orbit. An object, such as a javelin, that is projected horizontally will fall to earth describing a parabolic arc. A bullet fired by a rifle is projected at a higher velocity than the javelin so will travel further but must still fall to earth describing a parabolic arc. The part that is different here is the fact that the Earth is in fact round. For this reason the curvature of the Earth itself becomes significant, and allows the bullet to gain extra range before landing. If we could, however, fire a rocket with a large enough velocity, the rocket would cover enough distance in a short amount of time, so that the curvature of the Earths would fall out from under the rocket. And the rocket would continually miss the surface of the earth as it falls. The Earth would still cause a gravitational pull which would have the effect of continuously changing the rockets direction. If the direction is continuously changing while the speed remains constant then we have circular motion where the centripetal force is caused be the gravitational force. This is what we refer to as an object in orbit. In short, the rocket is always falling to the Earth, but it keeps missing Newton’s Cannon Fire a pig out of a cannon from the top of a high mountain. The pig falls towards the earth. If too low of a initial speed, the pig noseplants into the earth. However, there “is” a certain speed at which the pig falls toward the earth at the same rate as the earth's surface curves away. The pig then "misses" the earth and keeps "falling around it", (i.e. pigs in space) 15468.0 Geostationary Orbit A geostationary orbit is one in which a satellite orbits the earth at exactly the same speed as the earth turns and at the same latitude, specifically zero, the latitude of the equator. A satellite orbiting in a geostationary orbit appears to be hovering in the same spot in the sky, and is directly over the same patch of ground at all times. THE END Reviewing Concepts (10-13) Problems (20-28)