Download Universal Gravitation - White Plains Public Schools

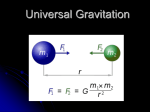
Universal
Gravitation
Unit 8
Lesson 1 : Newton’s Law of
Universal Gravitation
In 1687 Newton published Mathematical
Principles of Natural Philosophy
In this work he states :
Every particle in the Universe attracts
every other particle with a force that is
directly proportional to the product of their
masses and inversely proportional to the
square of the distance between them.
Fg =
G m1 m2
product of
masses
r2
distance
squared
Universal Gravitational
Constant
G has been measured experimentally. Its value is
G = 6.673 x 10-11 N.m2 / kg2
Measuring the Gravitational Constant (G)
Henry Cavendish (1798)
Gravitational attraction forms an
“action-reaction” pair.
F21 = -F12
The gravitational force exerted by a finitesize, spherically symmetric mass distribution
on a particle outside the distribution is the
same as if the entire mass of the distribution
were concentrated at the center.
Force exerted by the
Earth on a mass m near
the Earth’s surface.
Fg =
G ME m
RE2
Newton’s Test of the Inverse Square Law
The acceleration of the apple has
the same cause as the centripetal
acceleration of the moon.
aM
g
=
=
1/rM2
1/RE2
(6.37 x 106 m)2
(3.84 x 108 m)2
= 2.75 x 10-4
=
RE2
rM2
Centripetal acceleration of the Moon :
(2.75 x 10-4)(9.80 m/s2) = 2.70 x 10-3 m/s2
Newton calculated ac from its mean distance and
orbital period :
ac =
v2
(2prM / T)2
=
=
r
rM
=
4p2(3.84 x 108 m)
(2.36 x 106 s)2
= 2.72 x 10-3 m/s2
4p2rM
T2
Example 1
Three 0.300 kg billiard
balls are placed on a
table at the corners of
a right triangle.
Calculate the
gravitational force on
the cue ball (m1)
resulting from the
other two balls.
Free-Fall Acceleration and Gravitational Force
Equating mg and Fg :
mg =
G ME m
RE 2
g=
G ME
RE 2
Free-fall acceleration at a distance h above Earth’s surface :
g=
G ME
(RE + h)2
Example 2
Find the mass of the Earth and the average
density of the Earth.
Lesson 2 : Kepler’s Laws of Planetary Motion
Kepler’s First Law
All planets move in elliptical orbits
with the Sun at one focus.
F1 , F2 are foci located c from center
r1 + r2 = constant
2a = major axis
a = semimajor axis
2b = minor axis
b = semiminor axis
For planetary orbits, the Sun
is at one focus. There is
nothing at the other focus.
Eccentricity (e) of an Ellipse
describes the shape of
the ellipse
e=
c
a
e = 0.25
0<e<1
For circles, c = 0, e = 0.
Earth’s orbit e = 0.017
e = 0.97
Kepler’s Second Law
The radius vector drawn from the Sun
to a planet sweeps out equal areas in
equal time intervals.
Since t = r x F = 0, the angular
momentum L is constant.
In the time interval dt radius vector r sweeps out the
area dA, which equals half the area (r x dr) of the
parallelogram formed by vectors r and dr.
L
dA = ½ (r x dr) = ½ (r x v dt) =
dt
2Mp
constant
The radius vector
(r) from the Sun to
any planet sweeps
out equal areas in
equal times.
Kepler’s Third Law
The square of the orbital period of any
planet is proportional to the cube of the
semimajor axis of the elliptical orbit.
Since gravitational force provides centripetal force,
G MS MP
r2
=
MP v2
r
Since orbital speed = 2pr / T,
G MS
r2
=
(2pr / T)2
r
Solving for T2 ,
T2
4p2
GMS
=
4p2
r3
GMS
is a constant KS = 2.97 x 10-19 s2/m3
Replacing r with a,
T2 = KS a3
Example 1
Calculate the mass of the Sun using the fact
that the period of the Earth’s orbit around the
Sun is 3.156 x 107 s and its distance from the
Sun is 1.496 x 1011 m.
Example 2
Consider a satellite of mass m moving in a
circular orbit around the Earth at a constant
speed v and at an altitude h above the
Earth’s surface, as shown above.
a) Determine the speed of the satellite in terms of
G, h, RE (radius of Earth), and ME (mass of
Earth).
b) If the satellite is to be geosynchronous (that is,
appearing to remain over a fixed position on
the Earth), how fast is it moving through
space ?
Lesson 3 : Gravitational Potential Energy
Ug = mgh
only valid when the mass is
near the Earth’s surface,
where the gravitational
force is constant
What is the general form of the
gravitational potential energy function ?
Gravitational Force is Conservative
Work done by
gravitational force is
independent of path
taken by an object.
As particle moves from
point A to B, it is acted
upon by a central force F,
which is a radial force.
Work done depends
only on rf and ri.
Work done by force F is
always perpendicular to
displacement.
So, work done along
any path between
points A and B = 0
The total work done by
force F is the sum of the
contributions along the
radial segments.
rf
W=
 F(r) dr
ri
DU = Uf – Ui = -

rf
F(r) dr
ri
F(r) = -
GMEm
r2
negative sign
means force is
attractive
Negative of the
work done by
gravitational
force
Uf – Ui = GMEm

ri
rf
dr
1
= GMEm [ 2
r
r
Uf – Ui = - GMEm (
1
rf
-
1
ri
)
Taking Ui = 0 at ri = infinity,
U(r) = -
GMEm
r
(for r > RE)
Because of our choice of Ui, the
function U is always negative.
]
rf
ri
U(r) = -
GMEm
r
(for r > RE)
In General (for any two particles)
Gm1m2
U=r
Gravitational potential energy
varies as 1/r, whereas gravitational
force varies as 1/r2.
U becomes less negative as r increases.
U becomes zero when r is infinite.
Example 1
A particle of mass m is displaced through a
small vertical distance Dy near the Earth’s
surface. Show that in this situation the general
expression for the change in gravitational
potential energy given by
Uf – Ui = - GMEm (
1
rf
-
1
ri
)
reduces to the familiar relationship DU = mgDy.
Lesson 4 : Energy in Planetary and Satellite
Motion
E = KE + U
E=½
mv2
GMm
r
Newton’s Second Law
applied to mass m :
GMm
= ma =
r2
mv2
r
Multiplying both sides by r and dividing by 2,
½
mv2
GMm
=
2r
Substituting into E = ½
mv2
GMm
,
r
GMm
GMm
E=
2r
r
GMm
E= 2r
(total energy for
circular orbits)
GMm
E= 2r
total energy is negative
KE is positive and equal to half the
absolute value of U.
For elliptical orbits, we replace r with
semimajor axis a,
GMm
E= 2a
(total energy for
elliptical orbits)
In all isolated gravitationally bound
two-object systems :
Total energy is constant.
Total angular momentum is
constant.
Example 1
The space shuttle releases a 470 kg
communications satellite while in an orbit 280 km
above the surface of the Earth. A rocket engine on
the satellite boosts it into a geosynchronous orbit,
which is an orbit in which the satellite stays
directly over a single location on the Earth. How
much energy does the engine have to provide ?
Escape Speed
Minimum value of the initial speed
needed to allow the object to move
infinitely far away from the Earth.
When object reaches rmax, vf = 0, and
½
mvi2
GMEm
GMEm
= RE
RE
Solving for vi2,
vi2 = 2GME
(
1
1
RE
rmax
)
vi2 = 2GME
(
1
1
RE
rmax
If we let rmax  infinity,
vesc =
2GME
RE
)
Example 2
Calculate the escape speed from the Earth
for a 5000 kg spacecraft, and determine
the kinetic energy it must have at the
Earth’s surface in order to move infinitely
far away from the Earth.
Example 3 (AP 1984 #2)
Two satellites, of masses m and 3m, respectively,
are in the same circular orbit about the Earth’s
center, as shown in the diagram above. The
Earth has mass Me and radius Re. In this orbit,
which has radius 2Re, the satellites initially move
with the same orbital speed vo, but in opposite
directions.
a) Calculate the orbital speed vo of the satellites
in terms of G, Me, and Re.
b) Assume that the satellites collide head-on and
stick together. In terms of vo, find the speed
v of the combination immediately after the
collision.
c) Calculate the total mechanical energy of the
system immediately after the collision in
terms of G, m, Me, and Re. Assume that the
gravitational potential energy of an object is
defined to be zero at an infinite distance
from the Earth.
Example 4 (AP 1992 #3)
A spacecraft of mass 1,000 kg is in an elliptical orbit about
the Earth, as shown above. At point A the spacecraft is at a
distance rA = 1.2 x 107 m from the center of the Earth and
its velocity, of magnitude vA = 7.1 x 103 m/s, is
perpendicular to the line connecting the center of the Earth
to the spacecraft. The mass and radius of the Earth are
ME = 6.0 x 1024 kg and rE = 6.4 x 106 m, respectively.
Determine each of the following for the spacecraft
when it is at point A.
a) The total mechanical energy of the spacecraft,
assuming that the gravitational potential
energy is zero at an infinite distance from the
Earth.
b) The magnitude of the angular momentum of the
spacecraft about the center of the Earth.
Later the spacecraft is at point B on the
exact opposite side of the orbit at a distance
rB = 3.6 x 107 m from the center of the Earth.
c) Determine the speed vB of the spacecraft at
point B.
Suppose that a different spacecraft is at point A, a
distance rA = 1.2 x 107 m from the center of the
Earth. Determine each of the following.
d) The speed of the spacecraft if it is in a circular
orbit around the Earth.
e) The minimum speed of the spacecraft at point A
if it is to escape completely from the Earth.