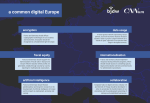
* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Survey
Document related concepts
Transcript
Management of Encrypted Databases --Homomorphic Encryption and Order-Preserving Indexing Dongxi Liu CSIRO ICT Centre [email protected] Outline • Overview of Encrypted Databases • Encrypted databases in our system • Our techniques • Homomorphic encryption scheme • Order-preserving indexing • Translation of SQL queries • Related works • The advantages of our method Databases – an appealing target to attack • Databases are widely used in information systems. • E.g., Web applications • Information in organizations is usually gathered in their databases • An attacker could get a large amount of information if a database is compromised • An example in Australia: • http://thenextweb.com/au/2012/08/15/hackers-grab500000-credit-card-details-australian-retailer-disasterwaiting-happen/ Database Security by Encryption • Obviously, encryption can be used to improve database security • even if the databases are outsourced to untrusted servers, or • the database servers are compromised. • A fragment of an encrypted table in our system A plain table The table after encryption Management of Encrypted Databases • However, encryption should not hamper the normal functionality of databases (e.g., performing queries) • Decrypting databases for answering queries is not acceptable • Ideally, queries should be executed directly over encrypted databases • Our method for encrypted database management is designed for this purpose The Architecture of Managing Encrypted Databases • The query proxy mediates communication between applications and encrypted databases • Our threat model • databases might be deployed on an untrusted or compromised machine. • the proxy and applications are in the trusted domain. SQL Queries and Cryptographic Techniques • Databases interact with applications mainly through SQL queries • Different types of queries • Equality query • “select a staff whose id is 10” • Secure hash or deterministic encryption • Range query • “select staffs whose incomes are in between 1000 and 2000” • Order-preserving encryption or indexing • Aggregate query (e.g., SUM and AVG) • “select the income sum of staffs” • Homomorphic encryption • Their combinations • “select the income average of staffs who join the company from year 2000 to year 2010” Features of SQL Operations • Addition on a large number of records • Multiplication on a few fixed number of table attributes • The bound of an aggregate query result is hard to determine for a long-standing databases • A query example • Select SUM(Rate*Hours) from Satff Name Address Peter 1 Vimiera Rd 70.0 36.32 Tom 2 Pembroke Rd 40.12 … Rate 53.2 Hours Homomorphic Encryption – Overview (1) • Described in the Australian Provisional Patent 2012902653 • Let K(n) be the key and v a value to encrypt • Enc(K(n), v) = (c1, …, cn) • Dec(K(n), (c1, …, cn)) = v • Additively homomorphic • Enc(K(n), v) = (c1, …, cn) • Enc(K(n), v’) = (c1’, …, cn’) • Dec(K(n), (c1+c1’, …, cn+cn’)) = v + v’ • Used when calculating sum Homomorphic Encryption – Overview (2) • Multiplicatively homomorphic • Enc(K(n), v) = (c1, …, cn) • Dec(K(n), (h*c1, …, h*cn)) = h*v, where h can be a real number • Used when calculating average • Enc(K(m), v’) = (c1’, …, cm’) • K(n) and K(m) can be two different keys • The multiplication of ciphertexts is their outer product (c1*c1’, …, cn*c1’ c1*c2’, …, cn*c2’ … c1*cm’, …, cn*cm’) • Steps of Dec(K(n), K(m), (c1*c1’,…, cn*cm’)) • Dec(K(n), (c1*ci’, …, cn*ci’ )) obtains v*ci’ (1≤ i ≤m) • Dec(K(n), (v*c1’, …, v*cm’)) returns v*v’. Homomorphic Encryption – Instance 1 • Key Generation • the key K(n) is a list of tuples of real numbers, [(k1, s1, t1), …, (kn, sn, tn)], where • n ≥ 3, ki ≠ 0 and ti ≠ 0 (1 ≤ i ≤ n-1), and kn+sn+ tn ≠ 0. • Encryption • Decryption • Variant: more s components in subciphertexts. Homomorphic Encryption - Correctness 1 • Simple proof • S = cn/(kn+tn+sn) = rn-1 • I = cn-1 – S*sn-1 = cn-1 – rn-1*sn-1= kn-1*tn-1*(r1+…+rn-2) • For i from 1 to n-2, we have • ci – S*si = ci – rn-1*si= ki*ti*v + ti*ri • (ci – S*si )/(L*ti) = ( ki*ti*vi + ti*ri)/(L*ti) = (ki*v + ri)/L • The sum of (ki*v + ri)/L from 1 to n-2 is • ((k1+…+kn-2)*v+r1+…+rn-2) /L= (L*v+r1+…+rn-2) /L • I/(L*kn-1*tn-1) = kn-1*tn-1*(r1+…+rn-2)/(L*kn-1*tn-1)= (r1+…+rn-2)/L • Finally, (L*v+r1+…+rn-2) /L - (r1+…+rn-2)/L = v Homomorphic Encryption - Instance 2 • Key Generation • the key K(n) is a list of tuples of real numbers, [(k1, s1, t1), …, (kn, sn, tn)], where • n ≥ 3, ki ≠ 0 and ti ≠ 0 (1 ≤ i ≤ n-1), , and kn+sn+ tn ≠ 0. • Encryption • Decryption • Variant: more s components in subciphertexts. Homomorphic Encryption - Correctness 2 • Simple proof • S = cn/(kn+tn+sn) = rn • c1 – S*s1 = c1 – rn*s1= k1*t1*v + k1*(r1-rn-1) • (c1 – S*s1)/(T*k1) = (t1*v + (r1-rn-1))/T, denoted by N1 • For i from 2 to n-1, we have • ci – S*si = ci – rn*si= ki*ti*v + ki *(ri-ri-1) • (ci – S*si )/(T*ki) = (ki*ti*v + ki *(ri-ri-1))/(T*ki) = (ti*v + (ri –ri-1))/T, denoted by Ni • The sum of Ni from 1 to n-1 is • ((t1+…+tn-1)*v+r1-rn-1+r2-r1…+rn-1-rn-2) /T= (T*v) /T=v Security Analysis – IND-CPA Instance 1 • cn and cn-1 is indistinguishable for every pair of values • Since they are not dependent on plaintexts • For ci (1≤i≤n-2) , we require ti *ki < si, v < rn-1 and ki *vi < ri • ci is dominated by the noises • Bigger noises means less probability to distinguish two ciphertexts • Maybe the hardness of LWE problem can also be used to prove the security. Conversion to a Public Key Scheme • Based on the subset sum problem, our scheme can be converted into a public key scheme. • The private key is the same K(n). • The public key is two sets of ciphertexts • The encryptions of zero • The encryptions of one • To encrypt v, • • • • • Step 1: Choose randomly an encryption of one Step 2: Multiply each subciphertexts in this encryption with v Step 3: Choose randomly a subset of zero encryptions Step 4: Add all zero encryptions in this subset Step 5: Add the ciphertexts in Step 2 and Step 4 Performance of Instance 1 • Encrypt the value 7985746234523.12 and decrypt the resulting ciphertext 200,000 times. • Key and noise configuration: • • • • 4 subciphertexs Each ki or ti has 4 digits (ddd.d) Each si has 8 digits (ddddddd.d) Each ri has have 6 digits (ddddd.d) • Key space size • The product of the space sizes of L, S, s1, t1, s2, t2, s3, t3, k3. • 104*108*(108*104*108*104*108*104*104)=1052, bigger than the key space size of AES-128. • Time on a Dell Latitude E4310 laptop in Eclipse • 422ms (HomoEnc: Java code uses data type double) • 8359ms (HomoEnc: Java code uses BigDecimal to represent value) • 859ms (AES-128 in SunJCE with ECB/PKCS5Padding) Order-Preserving Encryption (OPE) • If v1< v2, then OPE(k,v1) < OPE(k,v2) • Recall that OPE is used to process range queires • R. Agrawal et al. “Order Preserving Encryption for Numeric Data” (SIGMOD 2004) • Alexandra Boldyreva, et al. “ Order-Preserving Symmetric Encryption”. (EUROCRYPT 2009) Our Work: Order-Preserving Indexing (OPI) • If v1< v2, then OPI(k,v1) < OPI(k,v2) • Unlike OPE, it is not required to recover plaintexts from indexes. • Used together with the existing encryption schemes (e.g., AES or Homomorphic schemes) to manage encrypted databases • benefiting from the advance of existing encryption schemes. • Sensitivity of plaintexts • The absolute minimum between two consecutive plaintext values. • For example, the integer values can have sensitivity 1; the salary of “ddd.dd” (d is a digit from 0 to 9) have the sensitivity 0.01. • Configured in query proxy. The OPI Scheme: basic form • a*f(x)*x+b+noise • a, b and parameters in f are kept secret • a >0 • noise is sampled from the range [0, a*f(x+sens)*(x+sens)a*f(x)*(x)), where sens is the sensitivity of plaintexts; • f(x) > 0 for x ≠ 0; • f(x1) ≥ f(x2) for x1 > x2 ≥ 0 or x1 < x2 ≤ 0. • Denoted by nindexsens[a,b,f](x) The OPI Scheme: instances of f(x) • f(x) = |x|; • f(x) = logc(d + e * |x|), • where c > 1, d > 1 and e > 0. • f(x) = c * |x|/π + d * cos (|x|% π + π) + e, • where d > 0, c ≥ 2 * d, e ≥ d, and _ and % are the floor and modulo operators, respectively. • Composition of f(x): • logc(d + e * | g * |x|/ π + h * cos (|x|% + π) + i |), • where c > 1, d > 1, e > 0, h > 0, g ≥ 2 * h, i ≥ h. The OPI Scheme: An example • Input values: -10 to 10 with the sensitivity 1 • the indexing expression: 1600*log7(10+18*|x|)*x+317+noise The Indexing Scheme: programmability • Different plaintexts can be indexed with different expressions • Separate the distribution of plaintexts and ciphertexts • Make the indexes more robust • More secrets • The indexing program is not necessarily public, though the syntax is public The Indexing Scheme: a program The Indexing Scheme: a program Distribution of Ciphertexts Distribution of plaintext values Security of OPI • Like OPE, OPI is also vulnerable to Plaintext Chosen Attacks (CPA) • Since the order among ciphertexts reals information of plaintexts and the attack can be done by binary search • In our system, the proxy is placed in trusted domain to prevent CPAs. • We are still not clear if an attack happens to know some pairs of plaintexts and their indexes, what is the probability of obtaining plaintexts from other indexes. • But complex indexing programs can make it harder for performing such attacks Encrypted Database Management • Different table structures • Designed by application developers • E.g., a Staff table, with a Salary attribute • Created by the Query Proxy on the database services • E.g., a table with its name (Staff) hashed, and its attributes with hashed names • If an attribute does not support aggregate operations, its values can be encrypted with other schemes, like AES. • If an attribute does not support range queries, its values do not need to be indexed such as a Boolean attribute. Creation of Databases and Tables • Statements from applications • Statements from the proxy Data Insertion • Statements from applications • Statements from the proxy • where Enc(K(n),v) = (c1,…,cn) SQL Query (1) • Statements from applications • Statements from the proxy • cond’ is the translation of cond • Translation of conditions: • col_name < c Hash(k, col_name+“RngIdx”) < Index(c,0). • col_name = c Hash(k, col_name+“EqIdx”) = Hash(k, c). • col_name > c Hash(k, col_name+“RngIdx”) >= Index(c+sens,0). SQL Query (2) • Statements from applications • Statements from the proxy SQL Query (3) • Statements from applications • Statements from the proxy • One query might be translated into several ones • Another example: “select staffs whose salaries grater than average” Unsupported Queries • The conditions operating on several columns cannot be supported • E.g., the condition colnm1*colnm2+ colnm3 > colnm4*colnm5 • Our solution: by designing or adjusting table structures, almost all types of queries can be processed • E.g., we can add two columns in a table storing the OPI indexes of colnm1*colnm2+ colnm3 and colnm4*colnm5, respectively. • Need more work Performance of Querying Encrypted DB • The key configuration • • • • 4 subciphertexs Each ki or ti has 4 digits (ddd.d) Each si has 8 digits (ddddddd.d) Each ri has have 6 digits (ddddd.d) • The indexing expression • The table person(id int, name varchar(64), gender varchar(8), birthdate bigint, income numeric(10,2)) Performance of Insertion Performance of Query • select * from person where income > min and income < max Performance of Aggregate Query • select SUM(income) from person where income > min and income < max Related Works • Comparisons from the following perspectives • The native operations in DBMSs, such as SUM and AVG, should be used to support the operations on encrypted data. • The existing DBMSs should be used. • The database servers should not necessarily own the encryption keys. • The maximum sum of values in one table column should not be predetermined. • The maximum number of values should not be required. Related Works – Use of Native DBMS Operations • R. A. Popa, et al. “CryptDB: protecting confidentiality with encrypted query processing” . In ACM SOSP ’11. • From MIT • In this work, to calculate sum of values, they calculate the multiplication of encrypted data due to the use of Paillier’s homomorphic encryption system (EUROCRYPT 1999) • Multiplication is implemented as user-defined functions in particular DBMSs. • Multiplication is slower than addition. • Multiplication generates big values than addition. Related Works – Existing DBMSs (1) • T. Ge and S. Zdonik. “Answering aggregation queries in a secure system model”. VLDB 2007. • From Brown University • The values in multiple records are encrypted into one ciphertexts • • • • E.g., Salaries of four people are encrypted together . Their encrypted databases are not in the relational model. DBMSs need to be changed to process queries. Databases are hard to update. Related Works – Existing DBMSs (2) • Craig Gentry: Fully homomorphic encryption using ideal lattices. ACM STOC 2009. • From Stanford University and IBM Watson • Homomorphic operations must be mixed with a “ciphertext refresh step” to reduce noises in the ciphertexts • Since the somewhat homomorphic encryption scheme can only support a limited number of additions and multiplications • If Gentry’s idea is used, it means that the DBMSs must be changed to take into account “ciphertext refersh” when they executing the operations like SUM Related Works – Location of keys • In Oracle Database, AES can be used to encrypt some columns • Encryptions are transparent to users • That is, keys must be accessed by database server. • If the server is compromised, the key might be stolen, too. • AES is not a homomorphic encryption scheme. Related Works – Maximum Sum of Values • Zvika Brakerski, et al. “Fully Homomorphic Encryption from Ring-LWE and Security for Key Dependent Messages”. Crypto 2011. • From Weizmann Institute of Science • Craig Gentry: Fully homomorphic encryption using ideal lattices. ACM STOC 2009. • From Stanford University and IBM Watson • Other homomorphic encryption schemes • Their correctness asks the sum of one table column not greater than the modulus (for addition) • That is, the maximum sum of plaintexts needs to be predetermined to use these schemes. • Big modulus leads to big ciphertexts. • The maximum sum is hard to determine for long-standing databases. Related Works – Maximum number of Values • R. Agrawal, et al. “Order preserving encryption for numeric data”. ACM SIGMOD 2004. • From IBM Research • Their OPE scheme needs to know the total number of plaintexts (or the values in a table column) • This number might change for a table column after a longperiod of time Some Ideas for Collboration • Security Analysis • Both homomorphic encrtyption and order-preserving indexing schemes • Application of homomorphic encryption in big data processing platform • Dealing with scalability of multiplication • Appling homomorphic encryption to secure outsourced computing to clouds (e.g., data mining algorithm) Conclusion • Our techniques have the better usability for practical applications. • Homomorphic encryption scheme • Order-preserving index scheme • Translation of Query rewriting • A demo system is publically available • http://150.229.2.229/familySys/home Thanks!