Download Blackbody radiation Temperature of stars

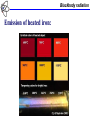
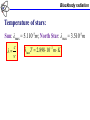
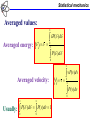
Lecture_02: Outline
Thermal Emission
 Blackbody radiation, temperature
dependence, Stefan’s law, Wien’s law
 Statistical mechanics, Boltzmann
distribution, equipartition law
 Cavity radiation, Rayleigh-Jeans classical
formula
Blackbody radiation
Matter under irradiation:
Blackbody radiation
Colors of matter:
Absorbs everything: black
Reflects everything: white
Transparent for everything: no color
Absorbs everything, but yellow: yellow
Absorbs everything, but red: red
This is not an emission!
Blackbody radiation
Emission of heated iron:
Blackbody radiation
Emission of heated iron:
Blackbody radiation
Emission of heated iron:

c

Blackbody radiation
Stefan’s Law:
Radiancy, RT, is the total energy emitted per unit time per unit
area from a blackbody with temperature T
Spectral radiancy, RT(ν), is the radiancy between frequencies ν
and ν+dν


0
0
RT   RT ( )d   RT ( )d
RT  T 4
Stefan-Boltzmann constant:
  5.67 108 W m2 K 4
RT(λ)
Blackbody radiation
Wien’s displacement law:
 max  T
 max  cT 2.898 10
3
Blackbody radiation
Temperature of stars:
Sun: λmax = 5.1ּ10-7m; North Star: λmax = 3.5ּ10-7m

c

max T  2.898 10 m  K
3
Blackbody radiation
Temperature of stars:
Sun: λmax = 5.1ּ10-7m; North Star: λmax = 3.5ּ10-7m

c

max T  2.898 10 m  K
3
Sun: T = 5700K; North Star: T = 8300K
Blackbody radiation
Temperature of stars:
Sun: λmax = 5.1ּ10-7m; North Star: λmax = 3.5ּ10-7m

c

max T  2.898 10 m  K
3
Sun: T = 5700K; North Star: T = 8300K
Radiancy of stars:
RT  T 4
  5.67 108 W m2  K 4
Blackbody radiation
Temperature of stars:
Sun: λmax = 5.1ּ10-7m; North Star: λmax = 3.5ּ10-7m

c

max T  2.898 10 m  K
3
Sun: T = 5700K; North Star: T = 8300K
Radiancy of stars:
RT  T 4
  5.67 108 W m2  K 4
Sun: RT = 5.9ּ107 W/m2; North Star: RT = 2.71ּ108 W/m2
Statistical mechanics
Ideal gas:
Temperature is related to averaged
kinetic energy
1
3
2
KE  m v  kT
2
2
For each of projections
(degrees of freedom):
1
1
1
1
2
2
2
m v x  m v y  m vz  kT
2
2
2
2
Statistical mechanics
Theorem of Equipartition of Energy:
Each degree of freedom contributes ½kT to the
energy of a system, where possible degrees of
freedom are those associated with translation,
rotation and vibration of molecules
Statistical mechanics
Boltzmann Distribution:
Distribution function (number density) nV(E):
It is defined so that nV(E) dE is the number of
molecules per unit volume with energy between E
and E + dE
Probability P(E):
It is defined so that P(E) dE is the probability to
find a particular molecule between E and E + dE
nV (E )  n0 e
E kT
e E kT
P(E ) 
kT
Statistical mechanics
Free particle:
E  KE  mv 2
2
P (v ) 
e
 mv 2 2 kT
kT
Harmonic oscillator:
1
1
2
KE  m vx  kT
2
2
1
PE  kT
2
E  E  KE  PE  kT
Statistical mechanics
Averaged values:

Averaged energy: E  E 
 EP(E )dE
0

 P(E )dE
0

Averaged velocity:
v v 
 vP(v)dv
0

 P(v)dv
0


0
0
Usually:  P(E )dE   P(v)dv  1
Rayleigh-Jeans formula
Cavity radiation:
• A good approximation of
a black body is a small
hole leading to the inside
of a hollow object
• The hole acts as a perfect
absorber
Energy density, ρT(ν), is the energy contained in a unit volume of
the cavity at temperature T between frequencies ν and ν+dν
T ( )  RT ( )
Rayleigh-Jeans formula
Electromagnetic waves in cavity:
E = Emax sin(2πx/λ) sin(2πνt)
With metallic walls,
E = 0 at the wall (x = 0,a)!
a
Rayleigh-Jeans formula
Electromagnetic waves in cavity:
E = Emax sin(2πx/λ) sin(2πνt)
With metallic walls,
E = 0 at the wall (x = 0,a)!
Only standing waves
are possible!
2a/λ = n
2aν/c = n
a
n=1
n=2
n=3
n=4
Rayleigh-Jeans formula
Allowed frequencies:
ν = cn/2a
2a
(  d )
c
2a

c
1
2
3
4
5
n
Number of allowed waves, N(ν)dν, between frequencies ν and ν+dν
2a
N ( )d  2  d
c
Polarization
Rayleigh-Jeans formula
Polarization:
E = Emax sin(2πx/λ) sin(2πνt)
Two independent waves
for each ν, λ
Rayleigh-Jeans formula
One-dimensional case:
Three-dimensional case:
4a
N ( )d 
d
c
4a 3
N ( )d  3 2 2 d
c
Energy spectrum, ρT(ν)dν, is equal to the number of allowed wave
per unit volume times the energy of each wave
1
T ( )d  3 N ( )d  E
a
Each wave can be considered as a harmonic oscillator with
E  kT
Rayleigh-Jeans formula
Rayleigh-Jeans formula:
8 2 kT
T ( )d 
d
3
c