Download of a Star

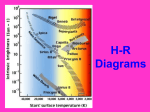
Chapter 8:
The Family of Stars
Motivation
We already know how to
determine a star’s
• surface temperature
• chemical composition
• surface density
In this chapter, we will learn how
we can determine its
• distance
• luminosity
• radius
• mass
and how all the different types of stars
make up the big family of stars.
Recent Picture from SDO
• A flare erupts from the sun's surface on March
30, in one of the first images sent back by
NASA's Solar Dynamics Observatory. Launched
in February, SDO is the most advanced
spacecraft ever designed to study the sun.
SDO provides solar images with clarity 10
times better than high-definition television.
Solar Flare -- SDO
Hipparchus -- ~ 150 BC
•
•
•
•
Credited with first star catalog
Introduced 360° in a circle
Introduced use of trigonometry
Using data from solar eclipse was able to
calculate distance to moon.
• Accurate star chart with 850 stars
• Created magnitude scale of 1 to 6
Hipparcos
• High Precision Parallax Collecting Satellite
• Mission – Map 100000 nearest stars to 2
milliseconds of arc
• Map another 1000000 stars to 10 milliseconds
of arc along with color information.
• Exceeded goals. 120000 stars to 1milliseconds
• Launched 1989 - Ended 1993
• Exceeded all goals. ESA European Space
Agency
Hipparcos Satallite
Distances to Stars
d in parsec (pc)
p in arc seconds
1
d = __
p
Trigonometric Parallax:
A star appears slightly shifted from
different positions of the Earth on its orbit.
The further away the star is (larger d),
the smaller the parallax angle p.
1 pc = 3.26 LY
The Trigonometric Parallax
Example:
Nearest star, a Centauri, has a parallax of p = 0.76 arc seconds
d = 1/p = 1.3 pc = 4.3 LY
The Limit of the Trigonometric Parallax Method:
With ground-based telescopes, we can measure
parallaxes p ≥ 0.02 arc sec
=> d ≤ 50 pc
=> This method does not work for
stars further away than 50 pc.
Intrinsic Brightness /
Absolute Magnitude
The more distant a light source
is, the fainter it appears.
The same amount of light falls
onto a smaller area at distance
1 than at distance 2 => smaller
apparent brightness
Area increases as square of distance => apparent
brightness decreases as inverse of distance squared
Intrinsic Brightness / Absolute
Magnitude
The flux received from the light is proportional to its
intrinsic brightness or luminosity (L) and inversely
proportional to the square of the distance (d):
L
__
F~ 2
d
Star A
Star B
Earth
Both stars may appear equally bright, although
star A is intrinsically much brighter than star B.
Distance and
Intrinsic Brightness
Example:
Recall:
Magn. Diff.
Intensity Ratio
1
2.512
2
2.512*2.512 = (2.512)2
= 6.31
…
…
5
(2.512)5 = 100
For a magnitude difference of
0.41 – 0.14 = 0.27, we find a
flux ratio of (2.512)0.27 = 1.28
Betelgeuse
App. Magn. mV = 0.41
Rigel
App. Magn. mV = 0.14
Distance and
Intrinsic Brightness
Rigel appears 1.28 times
brighter than Betelgeuse.
Betelgeuse
But, Rigel is 1.6 times
further away than
Betelgeuse.
Thus, Rigel is actually
(intrinsically) 1.28*(1.6)2
= 3.3 times brighter than
Betelgeuse.
Rigel
Absolute Magnitude
To characterize a star’s intrinsic
brightness or luminosity, we
define the Absolute Magnitude
(MV):
Absolute Magnitude MV =
Magnitude that a star would have
if it were at a distance of 10 pc.
Absolute Magnitude
Back to our example of
Betelgeuse and Rigel:
Betelgeuse
Betelgeuse Rigel
mV
0.41
0.14
MV
-5.5
-6.8
d
152 pc
244 pc
Difference in absolute magnitudes:
6.8 – 5.5 = 1.3
=> Luminosity ratio = (2.512)1.3 = 3.3
Rigel
The Distance Modulus
If we know a star’s absolute magnitude,
we can infer its distance by comparing
absolute and apparent magnitudes:
Distance Modulus
= mV – M V
= -5 + 5 log10(d [pc])
Distance in units of parsec
Equivalent:
d = 10(mV – MV + 5)/5 pc
The Size (Radius) of a Star
We already know: flux increases with surface
temperature (~ T4); hotter stars are brighter
But brightness also increases with size:
A
Star B will be
brighter than
star A.
B
Absolute brightness is proportional to the surface area
of the star, and thus its radius squared, L ~ R2.
Quantitatively:
L = 4 p R2 s T4
Surface area of the star
Surface flux due to a
blackbody spectrum
Example:
Polaris has just about the same spectral type
(and thus surface temperature) as our sun, but
it is 10,000 times brighter than our sun.
Thus, Polaris is 100 times larger than the sun.
This causes its luminosity to be 1002 =
10,000 times more than our sun’s.
Organizing the Family of Stars: The
Hertzsprung-Russell Diagram
We know:
Stars have different temperatures,
different luminosities, and different sizes.
Absolute mag.
or
Luminosity
To bring some order into that zoo of different
types of stars: organize them in a diagram of:
Luminosity versus Temperature (or spectral type)
Hertzsprung-Russell Diagram
Spectral type: O
Temperature
B
A
F
G
K
M
The Hertzsprung Russell Diagram
Most stars
are found
along the
Main
Sequence
The Hertzsprung-Russell Diagram
Same
temperature,
but much
brighter than
MS stars
→ Must be
much larger
→ Giant
Stars
Radii of Stars in the HertzsprungRussell Diagram
Betelgeuze
Rigel
Polaris
Sun
100 times smaller than the sun