* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download PowerPoint Presentation - Neutron stars, pulsars and black
Main sequence wikipedia , lookup
Nuclear drip line wikipedia , lookup
Stellar evolution wikipedia , lookup
Astronomical spectroscopy wikipedia , lookup
Gravitational lens wikipedia , lookup
Accretion disk wikipedia , lookup
Star formation wikipedia , lookup
Astrophysical X-ray source wikipedia , lookup
Hawking radiation wikipedia , lookup
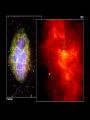
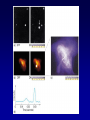
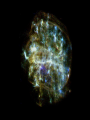
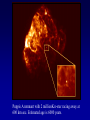
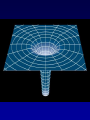
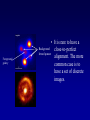
Last Section of AY4 • • • • • Last quiz: Thursday, June 5 Optional Final: Week of June 9 Neutron stars, pulsars, x-ray binaries Relativity Black Holes Neutron Stars • There is a last test of SNII theory • If the scenario is correct, there should be a VERY dense, VERY hot ball of neutrons left behind after the explosion. • Supported by neutron degeneracy (although there is an “atmosphere” of normal matter) This is called neutron “star” White dwarf 6000 km Neutron Star 10 km Neutron Stars: Predictions • Neutron star mass: > 1.4Mo • Neutron star radius: 10 - 80 km • Neutron star density: 1014 grams/cm3 100 million tons/thimble (all of humanity) • Initial Temperature: >2,000,000k • Neutron star remnant will be spinning rapidly and have a huge magnetic field Neutron Star Spins • The reason n-stars are predicted to be rapidly spinning is another Law of Physics called `Conservation of Angular Momentum’. • Linear momentum is a property of a moving object and is a vector quantity: of a moving object to remain in motion. • To change linear momentum p m v you need to exert a force on an object. Conservation of Angular Momentum • Any spinning object has `angular momentum’ which depends on how fast it is spinning and how the object’s mass is distributed. • `how fast’ -> w (greek letter omega) • `mass distribution’ -> Moment of inertia (I) L Iw Conservation of Angular Momentum • Conservation of angular momentum means: L initial L final Moment of Inertia Iiw i I f w f Ii w f I f wi Angular velocity Conservation of Angular Momentum • Think about those ice skaters. With arms out, a skater has a large moment of inertia. Pulling his/her arms in reduces the moment of inertia. Arms out: large I, low spin rate Arms in: small I, high spin rate Conservation of Angular Momentum • The moment of inertia for a solid sphere is: 2 2 I MR 5 • If a sphere collapses from a radius of 7x105km to a radius of 10km, by what factor does it’s spin rate increase? • Conservation of angular momentum means: Linitial L final Iiw i I f w f 2 2 2 MRi w i MR 2f w f 5 5 Ri2w i R 2f w f 5 2 R 7 10 9 w f w i w 4.9 10 wi i R 10 2 i 2 f • Sun rotates at 1 rev/month. Compress it to 10km and conserve L, it will spin up to 1890 revolutions/second (and fly apart) Magnetic Fields • Magnetic field lines are also conserved. When the core collapses, the field lines are conserved, and the density of the field lines goes way up . This is the strength of the magnetic field. Neutron Stars • The possibility of n-stars was discussed way back in the 1930’s but for many decades it was assumed they would be impossible to detect (why?) • But, in 1967, Jocelyn Bell and Tony Hewish set up a rickety barbed-wire fence in the farmland near Cambridge England to do some routine radio observations. LGMs • Bell and Hewish discovered a source in Vela that let out a pulse every 1.3 seconds. Then they realized is was accurate to 1.337 seconds, then 1.3372866576 seconds. They soon realized that the best clocks of the time were not accurate enough to time the object. They called it ‘LGM’. First Pulsar • Bell was a graduate student at the time. The source was assumed to be man made, but when no terrestrial source could be identified, they briefly considered an artificial extra-terrestrial source. • When a second source was discovered (Cass A) they announced the discovery as a new phenomenon. • The discovery led to a year of wild speculation, but explanations involving neutron stars quickly rose to the top. • A pulsing source with period of 0.033 seconds was discovered in the Crab nebula. • Big clue! Spin the Sun or Earth or a WD 30 times per second and they will be torn apart. • Need a small object with very large material strength. Pulsars • The new objects were named ‘pulsars’ and is was soon discovered that they were slowly slowing down -- this provided the answer to the mystery of why the Crab Nebula was still glowing. • There are now more than 1000 known pulsars in the Galaxy. Pulsars: The Lighthouse Model • So, what is the pulsing all about? • The key is to have a misalignment of the nstar magnetic and spin axes? • What do you call a rotating powerful magnetic field? Lighthouse model • A rotating magnetic field is called a generator. The pulsar is a dynamo which is typically about 1029 times more powerful than all the powerplants on Earth. The huge electric field rips particles off the surface and accelerates them out along the magnetic field axis. • The misalignment of the magnetic and spin axes results in a lighthouse-like effect as the beam sweeps past the Earth once per rotation period. Pulsars • The period of the Crab pulsar is decreasing by 3 x 10-8 seconds each day. The rotational energy is therefore decreasing and the amount of the decrease in rotation energy is equal to the luminosity of nebula. Old pulsars spin more slowly. • There is a mysterious cutoff in pulsar periods at 4 seconds. The Crab will slow to this in about 10 million years. The pulsar will turn off. Although the n-star will still be there, it will be essentially invisible. • Most pulsars have large space velocities. This is thought to be due to asymetric SNII explosions. Pulsars • Do all SN remnants have pulsars? • No - some SN remnants are from SNI • No - some rotating neutrons stars will have beams that don’t intersect the Earth Milli-sec Pulsars and X-ray Binaries • Since the first x-ray telescopes went into space on rockets it has been known that there are Luminous X-ray stars. • In 1982, the first of many milli-second pulsars was discovered • The two phenomenon are connected. • When a neutron stars has a close companion, it pulls material through the L1 point. This material flies down to the surface of the n-star and crashes onto the surface, releasing LOTS of gravitational potential energy. This energy comes out mostly as x-rays and is modulated with the n-stars spin. Mass-transfer and N-stars • Some of the x-ray binaries have allowed a measurement of the neutron star mass: In 10 of 11 cases, M=1.44Mo This is good! Neutron stars are all supposed to be more massive than the Chandrasekar limit and there is even reason to expect them to be close to this limit as that is what initiated the core collapse in a SNII Millisecond Pulsars • The discovery of pulsars that were spinning more than 100 times per second (the first was spinning 640 times per second) threw the field for a loop. When some millisecond pulsars were discovered in old star clusters it was even more confusing. • Eventually it was determined that all millisecond pulsars were in close binary systems and were `spun up’ by accreting material. Detecting Neutron Stars • Detecting n-stars via their photospheric emission is difficult. • N-stars are VERY hot, but have a tiny surface area so have low luminosity. • Initial temperature may be greater than 3,000,000k so a very young n-star will emit most of its Planck radiation in X-rays. • First isolated n-star observed in photospheric light was discovered in 1997. • Tsurface=700,000 • Estimated age is 106 years. • This is combined xray through visible light image • In 2002 there were about 6 isolated nstars known that are seen in the light of their Plank radiation. • Most are very nearby (<300 pc) and traveling VERY fast. Puppis A remnant with 2 millionK n-star racing away at 600 km.sec. Estimated age is 6000 years. Sun: R=105km density=6 gram/cm3 Neutron `star’: R=20km density=1014 Mass > 1.4Mo White Dwarf: R=6000km density=106 Mass < 1.4Mo Is there a limit to neutron degeneracy? • Yes! Gravity wins the final battle. The current best estimate for the maximum mass of a neutron-degenerate star is 3Mo. • If a neutron star exceeds this mass it will collapse into an infinitely small volume called a black hole. • But, this story starts with Einstein’s theories of special and general relativity. Special Relativity • Various experiments starting in the late 1800s suggested that the speed of light was constant, independent of the motion of the observer. • This is very counter-intuitive. • The spaceship traveling in the same direction of a photon measures the photon zooming away at the speed of light NO MATTER how fast the spaceship is traveling! Special Relativity • Einstein (and others before him) decided to take the speed of light as an invariant and not make any assumptions about the two properties that go into determining speed: Space and Time Time Dilation and Length Contraction • The invariance of the measured speed of light independent of the motion of the observer can be understood if: (1) Clocks run more slowly as speed increases. (2) Metersticks shrink as speed increases. Say What? Time Dilation • As your speed with respect to another observer increases, your watch runs more slowly than the observers. This is called `time dilation’ T T0 1 (v /c) 2 Note, when v<<c, T=T0 Time Dilation • As v approaches c, v/c -> 1 and the denominator goes to zero. Dividing by zero gives infinity. As v approaches c, time grinds to a stop! • Q. Suppose you measure an event that lasts for 1 second by your watch. What will your friend in a spaceship moving at 0.98c measure as the duration of the event? T T0 1 (0.98) 2 5.02T0 • Time has been stretched by a factor of 5 for your friend. Length Contraction • In the same way, metersticks (space) contracts in the direction of motion. L L0 1 (v /c) • But wait, there’s more! 2 Mass • Mass grows with speed. M M0 1 (v /c) 2 Constant Speed of Light • The shrinking rulers and slowing clocks conspire to let observers in any moving frame measure the same speed of light. The Reason Travel to other Galaxies will be Difficult • The slowing clocks and increasing mass conspire to make it impossible for objects with mass to ever reach the speed of light. • The increasing mass requires an ever-larger force to accelerate to larger speed and the force needed would become infinite. (F=ma) • Even if you could find the force, your clock would slow and slow and the last step would take and infinitely long time Is this right? • Yes! There are many tests of Special Relativity. • In particle accelerators mass increase and time dilation effects are routinely measured • There have been tests flying very accurate clocks in high-speed jets that show time dilation directly. • We might not be here if not for time dilation in the frame of cosmic rays called muons. General Relativity • Einstein’s theory of General Relativity is a theory of gravity • The basic idea is to drop Newton’s idea of a mysterious force between masses and replace it with the 4-dimensional SpaceTime Continuum General Relativity • In GR, mass (or energy) warps the spacetime fabric of space. • Orbits of planets around stars are not due to a central force, but rather the planets are traveling in straight lines through curved space Imagine tossing a shotput onto your bed and rolling marbles at different speeds and distances from the shotput. (also imagine that you have a frictionless blanket on the bed). The marbles that are moving slowly or close will fall down toward the shotput. If you look from above, it will appear as if the marbles were attracted to the shotput. Fabric of Space • This is a RADICALLY different view of the Universe and gravity • In regions where space is not strongly curved, GR reduces to Newton’s law of gravity • Einstein pointed out his new theory would explain the Precession of the Perihelion of Mercury The Deflection of Starlight • There were several other predictions of GR, one important one was that light rays would also follow straight lines through curved space. Tests of GR • In 1919, during a total eclipse of the Sun, the predicted deflection of starlight for stars near to the limb of the Sun was measured and Einstein became a household name. • GR also predicted that time would slow in strongly curved space. This was verified experimentally in 1958. Tests of GR • There is another long list of predictions made by GR -- in every case to date, they have verified the theory perfectly. The Bending of Light • The bending of light in GR leads to some very useful and interesting phenomenon. • One is the effect called a gravitational lens. • The light from a distant galaxy is bent by a large mass along the line of sight to to Earth. If everything is lined up perfectly, you get an “Einstein Ring”. Very useful for identifying and measuring “Dark Matter” Foreground galaxy • It is rare to have a Background close-to-perfect lensed quasar alignment. The more common case is to have a set of discrete images. On to Black Holes • The second very interesting aspect of light bending in General Relativity is the idea of Black Holes. It starts with the concept of escape velocity. Escape Velocity • Imagine feebly tossing a rocketship up in the air. It falls back to Earth because its kinetic energy was less than its gravitational potential energy. • However, toss it with a larger and larger velocity and it will go higher and higher before falling back to Earth. • There is a velocity above which it will not return to Earth -- this is the escape velocity. Escape Velocity • To determine the escape velocity from Earth you set the gravitational potential energy equal to kinetic energy and solve for velocity 2G M Vescape R Radius from which you want to escape Mass of the object from which you want to escape Escape Velocity • Note that the escape velocity doesn’t depend on the mass of the escaping body. • For the Earth, put in the mass and radius of the Earth (for escape from the surface of the Earth) and you get: Vesc= 11 km/sec = 25,000 miles/hr Escape Velocity • Now suppose you shrink the Earth to 1/100 of its current radius (at constant mass). What happens to Vesc? Vesc 2GM R 1 Vesc R As R goes up, Vesc goes down As R goes down, Vesc goes up Don’t forget the square root For this case, Vesc increases by 10x Escape Velocity • Reduce the radius of the Earth to 1cm and Vesc=c (speed of light) • In this new theory of Gravity, where photons are affected by gravity, if the escape velocity equals or exceeds the speed of light, that object can no longer be observed. This is a Black Hole Black Holes • The critical radius for which an object of a particular mass has an escape velocity of `c’ is called the Schwarzschild Radius. • This is also called • the `Event Horizon’. Schwarzschild Radius • You can easily calculate the Schwarzschild radius for any mass by setting Vesc=c Vesc 2MG c Rs 2MG 2MG c Rs 2 Rs c 2 • Every object has a radius at which it becomes a Black Hole Black Holes • But, it is VERY, VERY difficult to compress an object to its Schwarzschild radius. • For the Sun, you would have to somehow overcome thermal pressure, then edegeneracy, then neutron degeneracy. We know of no `cosmic vice’ that can do that. Black Holes • But, go back to a neutron star and we are building a pretty big vice. Thermal pressure has already been overcome as has edegeneracy pressure. • There is a limit to the pressure that can be generated by neutron degeneracy. Its hard to calculate, but is probably between 2Mo and 3Mo Black Holes • Think about the n-star core of a SNII explosion. If say 1.6Mo of material falls back, the core will exceed the neutron degeneracy limit and undergo collapse to zero volume (what?) zero volume. Black Holes • What is left behind? – The gravitationally force (i.e. a warp in spacetime) including a `singularity’ at the center of the warp – An Event Horizon with radius given by RSch=8.9km Hawking radiation Black Hole FAQs • What would happen if the Sun collapsed into a Black Hole, would the Earth be dragged in? • No, the gravitational force at the distance of the Earth would not change. • Is the Event Horizon a physical boundary? No, it is simply the distance from the center where the escape velocity of `c’. • What happens if a Black Hole absorbs some mass? As M increases, the Schwarzschild radius also increases. • Is there any reason to believe that Black Holes exist? You Bet! This would be great. But not too likely… Black Hole Evidence • The best stellar-mass cases are binary x-ray sources. Cygnus X-1 is a good example. Black Hole Evidence • Cyg X-1 is a bright x-ray source. Look there in the visual part of the spectrum, we see a 30Mo blue main-sequence star which is a spectroscopic binary with a period of 5.6 days. • The companion has a mass of between 5 and 10Mo. What is it? Cygnus X-1 • There is no sign of the companion at any wavelength so what is it? 1) A red giant would be easily seen 2) A main-sequence star would be seen with a little effort 3) Can’t be a WD because M>1.4Mo 4) Can’t be a n-star because M>3Mo Cygnus X-1 • By elimination, we are left with a black hole • The x-rays back this up. In an accreting WD we see UV radiation, in an n-star we see `soft’ x-rays, in Cyg X-1 we see `hard’ xrays because the accreting material falls into a deeper potential well. Stellar-mass Black Holes • We now have a few dozen excellent stellar-mass black hole candidates and few people doubt that such objects exist. • There was a `microlensing’ event in 1996 that was ascribed to a blackhole gravitationally lensing a background star. • There are various claims that x-ray transients are black holes accreting little bits of stuff. Supermassive Black Holes • Since the early 1960s extraordinarily energetic objects called `qso’s or `quasars’ have been identified a large distances and lookback times. • The only explanation astronomers could come up with for their energy source was accreting mass onto a large (>105Mo) black hole. Supermassive Black Holes • QSOs had large radio jets emitted at enormous velocities. • Eventually it became clear that QSOs were all located in the cores of galaxies and nearby counterparts were identified. • Cen A radio jets • The nearby systems allowed observations much closer to the central engine and over time the evidence for the black holes has become more direct The Galactic Center • After years of speculation about a possible supermassive black hole in the center of the Milky Way, work at Keck by Andrea Ghez at UCLA demonstrated convincingly in 1999 that we have a 2 million solar mass black hole at the center of the Galaxy. Supermassive Black Hole in the Galaxy • 2002 observations pretty much cinch the case for a 2.6 million solar mass black hole in the center of the galaxy. • See the movie!