Download Stellar Structure - Astronomy Centre : Research

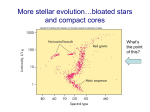
Stellar Structure
Section 6: Introduction to Stellar Evolution
Lecture 18 – Mass-radius relation for black dwarfs
Chandrasekhar limiting mass
Comparison with observation
Virial theorem explanation of mass limit
Thermal effects (approximate model)
Final fate of more massive remnants:
… mass loss, neutron stars, black holes
… observational evidence for ns, bh
Chandrasekhar’s results – repeat
• First calculations by Chandrasekhar, late 1920s, found two
curious results (see sketches on blackboard):
 as the total mass increases, the total radius decreases
 the total radius tends to zero for a finite total mass
• There is a critical mass, above which no solution can be found
(see blackboard) – the Chandrasekhar limiting mass
• In the absence of hydrogen, the limiting mass is 1.44 M
• Hard to measure masses and radii of white dwarfs – but available
observations lie close to model relationship (Handout 16)
• Chandrasekhar’s model now fully accepted
Virial theorem argument to explain
Chandrasekhar’s model
• Low-mass white dwarfs, with low central density, will be nonrelativistic: P  5/3
• Applying the virial theorem, and just looking at the scaling,
gives a balance between two terms, and yields a mass-radius
relation (see blackboard)
• As the central density increases, so does the mass (using the
mass-radius relation) – see blackboard
• Higher-mass white dwarfs therefore have higher central
densities and relativistic effects become important: P  4/3
• In this extreme case (see blackboard), there is balance for only
one mass: the Chandrasekhar mass
Thermal effects in surface layers – a
simple model
• Realistically: degree of degeneracy decreases towards surface,
with surface layers having low enough density to be completely
non-degenerate; smooth transition
• Model: fully degenerate core, ideal gas envelope, sharp
boundary between them
Non-degenerate envelope, ideal
gas equation of state
Black dwarf degenerate core,
non-relativistic degenerate
equation of state
Temperature at transition layer
(see blackboard for mathematics)
• Observed effective temperatures => radiative envelopes
• Observed mean density in envelopes => bound-free opacity
dominates – take Kramers’ law
• Neglect radiation pressure in envelope
• Take surface values for M, L, 
• Derive P-T relation in envelope
• Equate pressures at transition between core and envelope, and
use to eliminate the density at that radius
• Solve for the temperature at the transition radius
• Core ~isothermal – so this is ~core temperature, ~few106 K
• Implies XWD ≈ 0, and LWD comes from cooling of core
Final fate of stars more massive than
Chandrasekhar mass
• May lose enough mass via winds and superwinds to produce
white dwarf and planetary nebula: needs MMS < ~8 M
• More massive stars develop core with mass above
Chandrasekhar limit, and undergo core collapse in Type II
supernova explosion
• Collapse (implosion of core) → very high core densities, and
neutronisation, producing degenerate neutron gas
• Neutron degeneracy pressure can support core against gravity
• Remnant of SN explosion may be neutron star
Properties of neutron stars
• Neutron stars have masses not much more than the Chandra
mass, but radii much smaller than white dwarfs: RNS ~10 km
• Neutrons also Fermi particles, so equation of state similar to that of
white dwarfs, except that effects of special and general relativity
now important, especially in structure equations
• Expect maximum mass, as for WD
• Relativistic effects alone → Oppenheimer-Volkoff mass: ~0.72 M
• Must also include particle-particle interactions – poorly understood
at nuclear densities, so can only say that maximum mass is likely
to be between 2 and 3 M
• Some models shown on Handout 17
Core masses above NS limit
• If core mass above NS limit, nothing can halt collapse under
gravity
• Quantum effects probably prevent collapse to singularity with
infinite density, but unobservable:
• Remnant vanishes through its event horizon once escape
speed from surface exceeds speed of light (see blackboard)
• Event horizon occurs at Schwarzschild radius – remnant within
that radius is a black hole, detectable only by its (long-range)
gravitational field: no light can escape
• Black holes have only mass, angular momentum and charge
• (Quantum effects do allow Hawking radiation)
Observations of extreme remnants?
• Neutron stars:
 Detected in pulsars, low-mass X-ray binaries
 May have been directly detected by thermal x-ray emission
from hot surface in some X-ray binaries
 Masses from binaries all ~ Chandra mass (Handout 18),
suggesting formation by accretion onto a white dwarf
• Black holes:
 Cannot be observed directly
 More than a dozen high-mass X-ray binaries contain
compact remnants with masses above any possible neutron
star mass => detected gravitationally
That’s all, folks