Download Document

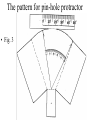
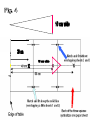
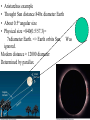
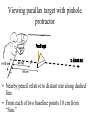
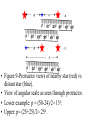
Angular Size & Parallax
• Fig. 1
Appearance and position of pin-hole
protractor
• Figure 2
The pattern for pin-hole protractor
• Fig. 3
Fold on dashed lines
Cut along solid black line to make a strip. Fold on dashed.
Cut object template and “Paper Mate Sharpwriter” holder
from part of an 8 ½ x 11 inch sheet of paper as shown
here.
Fig. 5 lower. Assembled ang. Size object and parallax target
• Tape pencil to middle of 10 cm wide object.
• Make object which holds pencil 4 cm high.
• Dashed line divides triangle symmetrically.
• Example: d=115 cm
angular size= 6o.
Phy.size th.=115cm(6o/57.3o)
= 12 cm
Actual size =13 cm
=100(13-12)/13=8%
•
•
•
•
Aristarchus example
Thought Sun distance 840x diameter Earth
About 0.5o angular size
Physical size =840(0.5/57.3)=
7xdiameter Earth. => Earth orbits Sun, Was
ignored.
Modern distance ≈ 12000 diameter
Determined by parallax
Aristarchus’ ideas were rejected. Why?
Common sense AND failure to observe stars’ parallax.
Parallax used to get distances of solar
system objects and stars.
• Fig. 6 Geometry of parallax experiment set-up
Layout for parallax observation versus
theory
Layout for parallax observation versus
theory
Viewing parallax target with pinhole
protractor
• Nearby pencil relative to distant star along dashed
line.
• From each of two baseline points 10 cm from
“Sun.”
• Figure 9-Protractor views of nearby star (red) vs
distant star (blue).
• View of angular scale as seen through protractor.
• Lower example: p = (50-24)/2= 13o.
• Upper: p= (25+25)/2= 25o.
•
•
•
•
Lower example previous page: p= 13o. R= 10 cm
d = 57.3 o (10/13 o) = 44.1 cm
Actual d = 43.3 cm
% error=100(44.1-43.1)/43.3 ≈ 2%
Finding the Distance of our Sun)
• Recall Copernicus found relative distances of
planets in solar system wrt Earth-Sun 1 AU.
• Measure parallax of Earth-Sun, Earth-Planets etc
• Observe from one side of Earth to other
• 93 million miles=150 million km.
The Long Quest for Stellar
Parallax
• Not until 1800’s.
• German astronomer Karl
Bessel
• First accurate measurement
of parallax of star 61 Cygni
in 1838.
• Tiny, p = 0.3 seconds of arc.
One arc sec= 1/3600 o
Distance pc=1/p parallax in arc sec
1 arc sec = 1/3600 degree
1 pc=200,000 AU=3.26 LY.
1 LY = 6trillion miles
Even the nearest stars are
amazingly far away.
• Nearest star parallax,
• p ~0.7725 arc sec
• 1/0.7725=1.3 pc away,
about four light years
travel time.
• > 200,000 times EarthSun distance
• The double star, Alpha
& Proxima Centaurus.
Example calculation of distance
with parallax.
• A star’s Π = 0.5 sec of arc.
• Distance in parsec = 1/Π in arc sec.
• Distance = 1/0.5 = 2 parsecs
= 6.52 light years or about 400,000 AU
= 39 trillion miles.
Progress in Measuring Parallax
• Limited by atmosphere “seeing.” and instrument.
• Bessel could measure distances to ~8 pc, ~25 ly,
only a few neighboring stars.
• 1989 Hipparchus satellite, to 0.001 arc sec;
d=1000pc= 3000 ly.
• Still only 3% of our Galaxy.
• 2011 Gaia space probe, will cover our whole
Galaxy.
End of Presentation