* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download The Degenerate Remnants of Massive Stars
Survey
Document related concepts
Observational astronomy wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Astronomical unit wikipedia , lookup
Expansion of the universe wikipedia , lookup
Kerr metric wikipedia , lookup
First observation of gravitational waves wikipedia , lookup
Transcript
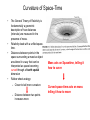
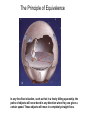
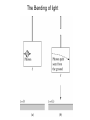
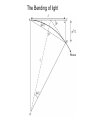
Black Holes and General Relativity • • • The General Theory of Relativity Intervals and Geodesics Black Holes The General Theory of Relativity Newton • Simple • Works (extremely) well • • Describes how things fall on earth Describes motion of solar system objects…predicted existence of Neptune • Unable to account for … • for 43”/century of observed 574”/century shift of mercury perihelion…hmmm? Einstein • Elegant • Works even better • Alters basic view of Universe • Mass space-time • Accounts for … • • additional 43”/century of observed 574”/century shift of mercury perihelion… Shifting of star positions during eclipse… Advance of the Perihelion of Mercury • • • Perihelion-nearest approach point of Mercury’s orbit advances due to effects from planets,etc… Newtonian Gravitation can not account for total observed shift of 574”/century….Planet Vulcan??? Einstein’s General Theory of relativity could fully account for the observed perihelion advance http://en.wikipedia.org/wiki/Tests_of_general_relativity http://en.wikipedia.org/wiki/Laplace%E2%80%93Runge%E2%80%93Lenz _vector http://en.wikipedia.org/wiki/Two-body_problem_in_general_relativity • Need to account for trivial precession of equinoxes 1.5 degree/century Advance of the Perihelion of Mercury www.math.toronto.edu/~colliand/426_03/Papers03/C_Pollock.pdf Curvature of Space-Time? Salvador Dali's "Soft Watch at Moment of First Explosion" Curvature of Space-Time • • • • The General Theory of Relativity is fundamentally a geometric description of how distances (intervals) are measured in the presence of mass. Relativity deals with a unified spacetime. Distances between points in the space surrounding a massive object are altered in a way that can be interpreted as space becoming curved through a fourth spatial dimension Rubber sheet analogy: – Closer to ball more curvature – Distance between two points increases more Mass acts on Spacetime, telling it how to curve Curved space-time acts on mass telling it how to move Curvature of Space-Time • Curved space….can see that….kinda • Curved time? The rate of flow of time is determined by the strength of the gravitational field where it is measured… Curvature of Space-Time Space and Time http://ion.uwinnipeg.ca/~vincent/4500.6-001/Cosmology/general_relativity.htm Gravity curves space ,eh? Looks like balls follow different curves to me!!... Curvature of Space-Time Space and Time Need to look at space and time….In space-time the balls trajectory do indeed have the same curvature… Curvature of Space-Time Space and Time Bullet and Ball initially take same paths in space. Why don’t they continue following same path if gravity is curving space? http://curious.astro.cornell.edu/question.php?nu mber=649 Bullet and Ball take different paths in space-time experience different curvature Curvature of Space-Time Space and Time Bullet and Ball initially take same paths in space. Why don’t they continue following same path if gravity is curving space? http://curious.astro.cornell.edu/question.php?nu mber=649 Bullet and Ball take different paths in space-time experience different curvature Curvature of Space-Time Since spacetime itself is curved even the trajectory of massless photons deviates from a “straight” line The Principle of Equivalence We’re in a “no gravity” state? The Principle of Equivalence In any free-float situation, such as that in a freely falling spaceship, the paths of objects will never bend in any direction when they are given a certain speed. These objects will move in completely straight lines. The Principle of Equivalence When the Earth (or a rocket) pushes on the spaceship, the tracks curve relative to the spaceship. The Principle of Equivalence The ball appears to move in the familiar curved path which we have come to view (since the time of Newton) as the effect of a gravitational force directed towards the center of the Earth. With the platform severed from its attachment to the Earth, the small house is in a free-fall situation. This time the ball will move in a straight line, unaffected by any socalled 'gravity' force. The Principle of Equivalence The Principle of Equivalence • Weak Equivalence principle – mg/mi is a constant • The Principle of Equivalence: All local, freely falling, nonrotating laboratories are fully equivalent for the performance of all physical experiments The Bending of light The Bending of light The Bending of light Gravitational Redshift and Time Dilation An outside observer, not in free-fall inside of the lab, would measure only the gravitational redshift (blueshift if the photon were going downward) Gravitational Redshift and Time Dilation • Light pulse generated at instant cable is released. In the time for the photon to cross the elevator cabin, the meter has attained a speed v=gt=gh/c. • Doppler blueshift should change meter’s frequency measurement by • In fact no frequency shift would be observed in accordance with principle of equivalence. The gravitational redshift exactly compensates by An outside observer, not in free-fall inside of the lab, would measure only the gravitational redshift (blueshift if the photon were going downward) Gravitational Redshift Calculation for a beam that escapes to infinity Gravitational Redshift and Time Dilation Gravitational Redshift Time Dilation Gravitational time dilation: Time passes more slowly as the surrounding space-time becomes more curved Intervals and Geodesics • General Relativity allows one to relate events (x,y,z,t) in spacetime in the presence of mass that results in the fabric of spacetime being curved!!! • T is the stress-energy tensor which evaluates the effect of a given distribution of mass and energy on the curvature of spacetime. • G is the Einstein Tensor for Gravity that mathematically describes the curvature of space-time. • Note that the Gravitational constant G and the speed of light play a role in the gravitational field equation. Field Equation: for calculating the geometry of space-time produced by a given distribution of mass and energy Worldlines and Light Cones • Worldline: The path followed by an object as it moves through spacetime. • Light Cone: worldline of photon originating at event A. The speed of light is taken to be 1. • What is the worldline for a freely falling object in response to the local curvature of spacetime? Spacetime Intervals, Proper Time and Proper Distance • • What is a “distance” in spacetime? Spatial distance between two points (x1,y1,z1) and (x2,y2,z2) in flat space • Spacetime interval: between two events (xA,yA,zA,tA) & (xB,yB,zB,tB) in flat spacetime s)2>0: timelike. Light has more than enough time to travel between the events A and B s)2=0. Lightlike separation. s)2<0: spacelike. Light does not have enough time to travel between the events Proper time: the time between two events that occurs at the same location. s is invariant under Lorentz transformations. An observer in another inertial frame S’ would measure the same interval between events A and B Proper Distance: The distance measured between two events A and B in a reference frame for which they occur simultaneously (tA=tB). The Metric for Flat Spacetime • Metric for flat 3-dimensional space • Path length for arbitrary path • • Straightest possible line between points minimizes length Metric for flat spacetime • Total interval along worldline •The interval measured along any timelike interval is the proper time multiplied by c. •The proper time along any lightlike worldline is zero •The proper time along any spacelike worldline is undefined •In flat spacetime, the interval measured along a straight timelike worldline is a maximum!!! The Metric for Flat Spacetime Curved Spacetime and the Schwarzschild Metric • Flat spacetime metric in polar coordinates •Mass acts on spacetime, telling it how to curve •Spacetime in turn acts on mass, telling it how to move • Schwarzschild metric in space time curved by a spherical body of mass M where r>R •Geodesic: “Straightest” possible worldline. In a flat spacetime a geodesic is a straight worldline. In a curved spacetime a geodesic will be curved. •Any freely falling particle (including a photon) follows the straightest possible worldline, a geodesic, through spacetime. For a massive particle the geodesic has a maximum or a minimum interval, while for light , the geodesic has a null interval. Shortest distance between two points may not be a straight line The Schwarzschild metric •Consider a sphere of radius R and mass M placed at the origin of the coordinate system. The coordinate r does NOT represent distance from the origin. A concentric sphere whose surface is at r would have a surface area 4r2. •A Flamm paraboloid helps “visualize” this curvature. Remember that “you” would be contained in the curved spacetime and you cannot directly “view” the curvature into the 4th dimension…. •Proper distance along a radial line •Proper Time at radial coordinate r • http://en.wikipedia.org/wiki/Schwarzschild_ metric • • http://casa.colorado.edu/~ajsh/schwp.html http://people.hofstra.edu/Stefan_Waner/diff_geo m/Sec15.html http://channel.nationalgeographic.com/episode/journey-to-theedge-of-the-universe-3023/Overview#tab-interactive The Orbit of a Satellite • Starting with Schwarzschild metric with dr=0, d=0 and d=dt where v/r Tests of General Relativity http://en.wikipedia.org/wiki/Tests_of_general_relativity • Classical Tests – Perihelion Precession of Mercury – Deflection of light by the Sun – Gravitational Redshift of Light • Modern Tests – Gravitational Lensing – Light travel time delay testing – Equivalence Principle tests • Gravitational redshift • Lunar Ranging… – Frame dragging tests • Strong Field Tests (Neutron stars,Black holes) • Gravitational Wave Detectors • Cosmological Tests Gravitational Lens Gravitational Lens “Einstein Cross” Gravitational Lens Studies at the U Gravitational Lens Studies at the U Black Holes • In 1783 John Mitchell pondered that the escape velocity from the surface of a star 500 times larger than the sun with the same average density would equal the speed of light. v esc = 2GM /r = 2G(500MÄ ) /7.93RÄ = c • • • Light would not be able to escape from such a star!!!! Naïve solution of Newtonian escape velocity equation for c gives a radius of R=2GM/c2 for a star whose escape velocity equals the speed of light. R=2.95(M/M) km….kinda small!!! In 1939 J. Robert Oppenheimer and Hartland Snyder described the ultimate gravitational collapse of a massive star that has exhausted its sources of nuclear fusion. They pondered what happened to the cores of stars whose mass exceeded the limit of neutron stars.. In 1967 the term “black hole” was coined By John Archibald Wheeler The Schwarzschild Radius • Consider the Schwarzschild metric • When the radial coordinate of the star’s surface has collapsed to RS=2GM/c2 the square roots in the metric go to zero. RS is known as the Schwarzschild Radius. • • • • At r=RS the behavior of space and time is “remarkable”…. The proper time measured by a clock here is d=0. Time has slowed to a complete stop! As measured from a vantage point far away. From this viewpoint nothing ever happens at the Scwarzschild radius Does this mean that even light is frozen in time??? The speed of light by an observer suspended above the star must always be c. But from far away we can determine that light is delayed as it moves through curved spacetime… •The apparent speed of light, the rate at which the spatial coordinates of a photon change, is called the coordinate speed of light. For light ds=0. • For dd=0, we have •In flat spacetime dr/dt~c, however at r=RS dr/dt=0 Light does appear frozen in time at the Schwarzschild radius!!!