Download Data Mining Tutorial

Data Mining Tutorial
D. A. Dickey
Data Mining - What is it?
•
•
•
•
Large datasets
Fast methods
Not significance testing
Topics
– Trees (recursive splitting)
– Regression & Logistic Regression
– Neural Networks
– Association Analysis
– Nearest Neighbor
– Clustering
– Etc.
If the Life Line is long and deep, then this
represents a long life full of vitality and
health. A short line, if strong and deep,
also shows great vitality in your life and
the ability to overcome health problems.
However, if the line is short and shallow,
then your life may have the tendency to
be controlled by others
http://www.ofesite.com/spirit/palm/lines/linelife.htm
Wilson & Mather JAMA 229 (1974)
X=life line length
Y=age at death
proc sgplot;
scatter Y=age X=line;
reg Y=age X=line;
run ;
Result: Predicted Age at Death = 79.24 – 1.367(lifeline)
(Is this “real”??? Is this repeatable???)
We Use LEAST SQUARES
Squared residuals sum to 9609
Distribution of t
Under H0
Estimated slopes vary in repeated samples.
Standard deviation (estimated) of sample slopes = “Standard error”
Compute t = (estimate – hypothesized)/standard error
p-value is probability of larger |t| when hypothesis is correct (e.g. 0 slope)
p-value is sum of two tail areas.
Traditionally p<0.05 implies hypothesized value is wrong.
p>0.05 is inconclusive.
proc reg data=life;
model age=line;
run;
Parameter Estimates
Variable DF
Intercept 1
Line
1
Parameter
Estimate
79.23341
-1.36697
Standard
Error
14.83229
1.59782
H0:slope=0
-0.86
t Value Pr > |t|
5.34
<.0001
-0.86
0.3965
Area 0.19825
Area 0.19825
0.39650
0.86
Conclusion: insufficient evidence against the hypothesis of no linear relationship.
H0:
H1:
H0: Innocence
H1: Guilt
Beyond reasonable
doubt
P<0.05
H0: True slope is 0
(no association)
H1: True slope is not 0
P=0.3965
Need estimate of variability around the true line. True variance is 
Estimate uses sums of squared residuals (SS).
Sum of squared residuals from the mean is “SS(total)”
Sum of squared residuals around the line is “SS(error)”
2
9755
9609
(1) SS(total)-SS(error) is SS(model)
=
146
(2) Variance estimate is SS(error)/(degrees of freedom) = 200
(3) SS(model)/SS(total) is R2, i.e. proportion of variablity
“explained” by the model.
Analysis of Variance
Source
Model
Error
Corrected Total
Root MSE
14.14854
DF
1
48
49
Sum of
Squares
146.51753
9608.70247
9755.22000
R-Square
0.0150
Mean
Square
146.51753
200.18130
F Value
0.73
Pr > F
0.3965
Trees
•
•
•
•
•
•
•
•
A “divisive” method (splits)
Start with “root node” – all in one group
Get splitting rules
Response often binary
Result is a “tree”
Example: Loan Defaults
Example: Framingham Heart Study
Example: Automobile fatalities
Recursive Splitting
Pr{default} =0.007
Pr{default} =0.012
Pr{default} =0.006
X1=Debt
To
Income
Ratio
Pr{default} =0.0001
Pr{default} =0.003
No default
Default
X2 = Age
Some Actual Data
• Framingham Heart
Study
• First Stage Coronary
Heart Disease
– P{CHD} = Function of:
• Age - no drug yet! 
• Cholesterol
• Systolic BP
Import
Example of a “tree”

Pruning options:
N=4
Gini for splits
Assessment = Avg. Sq. Err.
How to make splits?
• Which variable to use?
• Where to split?
– Cholesterol > ____
– Systolic BP > _____
• Goal: Pure “leaves” or “terminal nodes”
• Ideal split: Everyone with BP>x has
problems, nobody with BP<x has
problems
How to make
splits?

Contingency
tables
Heart Disease
No
Yes
180 ?
240?
Low
BP
High
BP
95
5
Heart Disease
No
Yes
100
100
75
55
150
45
50
DEPENDENT (effect)
25
100
100
75
25
150
50
INDEPENDENT (no effect)
c2 Test Statistic
• Expect 100(150/200)=75 in upper left if
independent (etc. e.g. 100(50/200)=25)
Heart Disease
No
Yes
Low
BP
High
BP
(observed  exp ected ) 2
c  allcells
exp ected
2
95
(75)
55
(75)
5
(25)
45
(25)
100
150
50
200
100
WHERE IS HIGH BP CUTOFF???
2(400/75)+
2(400/25) =
42.67
Compare to
Tables –
Significant!
Measuring “Worth” of a Split
• P-value is probability of Chi-square as
great as that observed if independence is
true. (Pr {c2>42.67} is 6.4E-11)
• P-values all too small.
• Logworth = -log10(p-value) = 10.19
• Best Chi-square  max logworth.
Logworth for Age Splits
?
Age 47 maximizes logworth
How to make splits?
• Which variable to use?
• Where to split?
– Cholesterol > ____
– Systolic BP > _____
• Idea – Pick BP cutoff to minimize p-value
for c2
• What does “signifiance” mean now?
Multiple testing
• 50 different BPs in data, 49 ways to split
• Sunday football highlights always look
good!
• If he shoots enough times, even a 95% free
throw shooter will miss.
• Tried 49 splits, each has 5% chance of
declaring significance even if there’s no
relationship.
Multiple testing
a=
Pr{ falsely reject hypothesis 2}
a=
Pr{ falsely reject hypothesis 1}
Pr{ falsely reject one or the other} < 2a
Desired: 0.05 probabilty or less
Solution: use a = 0.05/2
Or – compare 2(p-value) to 0.05
Multiple testing
•
•
•
•
•
•
50 different BPs in data, m=49 ways to split
Multiply p-value by 49
Bonferroni – original idea
Kass – apply to data mining (trees)
Stop splitting if minimum p-value is large.
For m splits, logworth becomes
-log10(m*p-value)  ! ! !
Validation
• Traditional stats – small dataset, need all
observations to estimate parameters of
interest.
• Data mining – loads of data, can afford
“holdout sample”
• Variation: n-fold cross validation
– Randomly divide data into n sets
– Estimate on n-1, validate on 1
– Repeat n times, using each set as holdout.
Pruning
• Grow bushy tree on the “fit data”
• Classify validation (holdout) data
• Likely farthest out branches do not improve,
possibly hurt fit on validation data
• Prune non-helpful branches.
• What is “helpful”?
• What is good discriminator
criterion?
Goals
• Split if diversity in parent “node” > summed
diversities in child nodes
• Prune to optimize
– Estimates
– Decisions
– Ranking
• in validation data
Accounting for Costs
• Pardon me (sir, ma’am) can you spare
some change?
• Say “sir” to male +$2.00
• Say “ma’am” to female +$5.00
• Say “sir” to female -$1.00 (balm for
slapped face)
• Say “ma’am” to male -$10.00 (nose splint)
Including Probabilities
Leaf has Pr(M)=.7, Pr(F)=.3.
You say:
Sir
Ma’am
True
Gender
M
0.7 (2)
0.7 (-10)
0.3 (5)
F
+$1.10
-$5.50
Expected profit is 2(0.7)-1(0.3) = $1.10 if I say “sir”
Expected profit is -7+1.5 = -$5.50 (a loss) if I say “Ma’am”
Weight leaf profits by leaf size (# obsns.) and sum
Prune (and split) to maximize profits.
Additional Ideas
• Forests – Draw samples with replacement
(bootstrap) and grow multiple trees.
• Random Forests – Randomly sample the
“features” (predictors) and build multiple
trees.
• Classify new point in each tree then
average the probabilities, or take a
plurality vote from the trees
Lift
3.3
* Cumulative Lift Chart
- Go from leaf of most
to least predicted
1
response.
- Lift is
proportion responding in first p%
overall population response rate
Regression Trees
• Continuous response Y
• Predicted response Pi constant in regions
i=1, …, 5
Predict 80
Predict 50
X2
Predict
130
Predict 100
X1
Predict
20
• Prediction PREDi in cell i.
• Yij jth response in cell i.
• Split to minimize Si Sj (Yij-PREDi)2
Predict 80
Predict 50
Predict
130
Predict 100
Predict
20
• Predict Pi in cell i.
• Yij jth response in cell i.
• Split to minimize Si Sj (Yij-Pi)2
Real data example: Traffic accidents in Portugal*
Y = injury induced “cost to society”
Help - I ran
Into a “tree”
Help - I ran
Into a “tree”
* Tree developed by Guilhermina Torrao, (used with permission)
NCSU Institute for Transportation Research & Education
An alternative method:
Multiple Regression
Issues:
(1) Testing joint importance versus individual significance
Two engine plane can still fly if engine #1 fails
Two engine plane can still fly if engine #2 fails
Neither is critical individually
Jointly critical (can’t omit both!!)
(2) Prediction versus modeling individual effects
(3) Collinearity (correlation among inputs)
Example: Hypothetical company’s sales Y depend on TV
advertising X1 and Radio Advertising X2.
Y = b0 + b1X1 + b2X2 +e
Data Sales; length sval $8; length cval $8;
input store TV radio sales;
(more code)
cards;
Sales
1 869 868 9089
2 836 820 8290
(more data)
40 969 961 10130
Radio
TV
proc g3d data=sales;
scatter radio*TV=sales/shape=sval color=cval zmin=8000;
run;
Conclusion: Can predict well with just TV, just radio, or both!
SAS code:
proc reg data=next; model sales = TV radio;
Analysis of Variance
Source
Model
Error
Corrected Total
Root MSE
Sum of
Squares
32660996
1683844
34344840
DF
2
37
39
213.32908
Mean
Square
16330498
45509
R-Square
F Value
358.84
Pr > F
<.0001 (Can’t omit both)
0.9510  Explaining 95% of variation in sales
Parameter Estimates
Variable
Intercept
TV
radio
DF
1
1
1
Parameter
Estimate
531.11390
5.00435
4.66752
Standard
Error
359.90429
5.01845
4.94312
t Value
1.48
1.00
0.94
Pr > |t|
0.1485
0.3251 (can omit TV)
0.3512 (can omit radio)
Estimated Sales = 531 + 5.0 TV + 4.7 radio with error variance 45509 (standard deviation 213).
TV approximately equal to radio so, approximately
Estimated Sales = 531 + 9.7 TV
or
Estimated Sales = 531 + 9.7 radio
Summary:
Good predictions given by
Sales = 531 + 5.0 x TV + 4.7 x Radio or
Sales = 479 + 9.7 x TV
or
Sales = 612 + 9.6 x Radio or
(lots of others)
Why the confusion?
The evil Multicollinearity!!
(correlated X’s)
Multicollinearity can be diagnosed by looking at principal components
(axes of variation)
Variance along PC axes  “eigenvalues” of correlation matrix
Direction axes point  “eigenvectors” of correlation matrix
Principal Component
Axis 1
Proc Corr; Var TV radio sales;
Pearson Correlation Coefficients, N = 40
Prob > |r| under H0: Rho=0
TV
radio
sales
TV
1.00000
0.99737
<.0001
0.97457
<.0001
radio
0.99737
<.0001
1.00000
0.97450
<.0001
sales
0.97457
<.0001
0.97450
<.0001
1.00000
TV $
Principal Component
Axis 2
Radio $
Grades vs. IQ and Study Time
Data tests; input IQ Study_Time Grade; IQ_S = IQ*Study_Time;
cards;
105
10
75
110
12
79
120
6
68
116
13
85
122
16
91
130
8
79
114
20
98
102
15
76
;
Proc reg data=tests; model Grade = IQ;
Proc reg data=tests; model Grade = IQ Study_Time;
Variable
Intercept
IQ
Variable
Intercept
IQ
Study_Time
DF
1
1
Parameter
Estimate
62.57113
0.16369
Standard
Error
48.24164
0.41877
t Value
1.30
0.39
Pr > |t|
0.2423
0.7094
DF
1
1
1
Parameter
Estimate
0.73655
0.47308
2.10344
Standard
Error
16.26280
0.12998
0.26418
t Value
0.05
3.64
7.96
Pr > |t|
0.9656
0.0149
0.0005
Contrast:
TV advertising looses significance when radio is added.
IQ gains significance when study time is added.
Model for Grades:
Predicted Grade = 0.74 + 0.47 x IQ + 2.10 x Study Time
Question:
Does an extra hour of study really deliver 2.10 points for
everyone regardless of IQ? Current model only allows this.
proc reg; model Grade = IQ Study_Time IQ_S;
Source
Model
Error
Corrected Total
Root MSE
Variable
Intercept
IQ
Study_Time
IQ_S
DF
Sum of
Squares
Mean
Square
3
4
7
610.81033
31.06467
641.87500
203.60344
7.76617
2.78678
R-Square
F Value
Pr > F
26.22
0.0043
0.9516
DF
Parameter
Estimate
Standard
Error
t Value
Pr > |t|
1
1
1
1
72.20608
-0.13117
-4.11107
0.05307
54.07278
0.45530
4.52430
0.03858
1.34
-0.29
-0.91
1.38
0.2527
0.7876
0.4149
0.2410
“Interaction” model:
Predicted Grade =
72.21  0.13 x IQ  4.11 x Study Time + 0.053 x IQ x Study Time
= (72.21  0.13 x IQ )+(  4.11 + 0.053 x IQ )x Study Time
IQ = 102 predicts
Grade = (72.21-13.26)+(5.41-4.11) x Study Time = 58.95+ 1.30 x Study Time
IQ = 122 predicts
Grade = (72.21-15.86)+(6.47-4.11) x Study Time = 56.35 + 2.36 x Study Time
Slope = 2.36
Slope = 1.30
(1)
(2)
(3)
(4)
Adding interaction makes everything insignificant (individually) !
Do we need to omit insignificant terms until only significant ones remain?
Has an acquitted defendant proved his innocence?
Common sense trumps statistics!
Logistic Regression
•
•
•
•
“Trees” seem to be main tool.
Logistic – another classifier
Older – “tried & true” method
Predict probability of response from input
variables (“Features”)
• Linear regression gives infinite range of
predictions
• 0 < probability < 1 so not linear regression.
Example: Seat Fabric Ignition
• Flame exposure time = X
• Ignited Y=1, did not ignite Y=0
– Y=0, X= 3, 5, 9 10 ,
13,
16
– Y=1, X =
7, 11, 12, 14, 15, 17, 25, 30
• Q=(1-p1)(1-p2)p3(1-p4)(1-p5)p6p7(1-p8)p9p10(1p11)p12p13p14
• p’s all different : pi=exp(a+bXi) /(1+exp(a+bXi))
• Find a,b to maximize Q(a,b)
• Logistic idea: Map p in (0,1) to L in whole
real line
• Use L = ln(p/(1-p))
• Model L as linear in temperature, e.g.
• Predicted L = a + b(temperature)
• Given temperature X, compute L(x)=a+bX
then p = eL/(1+eL)
• p(i) = ea+bXi/(1+ea+bXi)
• Write p(i) if ignition, 1-p(i) if not
• Multiply all n of these together, find a,b to
maximize
Generate Q for array of (a,b) values
DATA LIKELIHOOD;
ARRAY Y(14) Y1-Y14; ARRAY X(14) X1-X14;
DO I=1 TO 14; INPUT X(I) y(I) @@; END;
DO A = -3 TO -2 BY .025;
DO B = 0.2 TO 0.3 BY .0025;
Q=1;
DO i=1 TO 14;
L=A+B*X(i); P=EXP(L)/(1+EXP(L));
IF Y(i)=1 THEN Q=Q*P; ELSE Q=Q*(1-P);
END; IF Q<0.0006 THEN Q=0.0006; OUTPUT; END;END;
CARDS;
3 0 5 0 7 1 9 0 10 0 11 1 12 1 13 0 14 1 15 1 16 0 17 1
25 1 30 1
;
Likelihood function (Q)
-2.6
0.23
Concordant pair 
Discordant Pair
IGNITION DATA
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Parameter
Intercept
TIME
DF
1
1
Estimate
-2.5879
0.2346
Standard
Error
1.8469
0.1502
Wald
Chi-Square
1.9633
2.4388
Pr > ChiSq
0.1612
0.1184
Association of Predicted Probabilities and Observed Responses
Percent Concordant
Percent Discordant
Percent Tied
Pairs
79.2
20.8
0.0
48
Somers' D
Gamma
Tau-a
c
0.583
0.583
0.308
0.792
Example:
Shuttle Missions
•
•
•
•
•
O-rings failed in Challenger disaster
Low temperature
Prior flights “erosion” and “blowby” in O-rings
Feature: Temperature at liftoff
Target: problem (1) - erosion or blowby vs. no
problem (0)
Example: Framingham
• X=age
• Y=1 if heart trouble, 0 otherwise
Framingham
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Parameter
DF
Intercept
age
1
1
Standard
Wald
Estimate
Error Chi-Square
-5.4639
0.0630
0.5563
0.0110
96.4711
32.6152
Pr>ChiSq
<.0001
<.0001
Neural Networks
X1
inputs
X2
X3
H1
(0,1)
Output = Pr{1}
H2
Logistic function of
X4
• Very flexible functions
• “Hidden Layers”
• “Multilayer
Perceptron”
Logistic functions
**
Of data
** (note: Hyperbolic
tangent functions are just
reparameterized logistic
functions)
Arrows represent linear
combinations of “basis
functions,” e.g. logistic
curves (hyperbolic tangents)
p1
p2
p3
b1
b2
Y
b3
Example:
Y = a + b1 p1 + b2 p2 + b3 p3
Y = 4 + p1+ 2 p2 - 4 p3
(-10)
3
-0.4
0.8
X1
(-13)
0
(-1)
-1
0.25
X2
P
-0.9
0.01
(20)
2.5
(“biases”)
A Complex Neural Network Surface
• Should always use holdout sample
• Perturb coefficients to optimize fit (fit data)
– Nonlinear search algorithms
• Eliminate unnecessary complexity using
holdout data.
• Other basis sets
– Radial Basis Functions
– Just normal densities (bell shaped) with
adjustable means and variances.
A Combined Example
Cell Phone Texting Locations
Black circle:
Phone moved > 50 feet in first two
minutes of texting.
Green dot:
Phone moved < 50 feet. .
Tree
Neural Net
Logistic Regression 

Three Models
Training Data
Lift Charts
Validation Data
 Lift Charts
Resulting
 Surfaces
Unsupervised Learning
• We have the “features” (predictors)
• We do NOT have the response even on a
training data set (UNsupervised)
• Clustering
– Agglomerative
• Start with each point separated
– Divisive
• Start with all points in one cluster then spilt
– Direct
• State # clusters beforehand
EM  PROC FASTCLUS
• Step 1 – find (50) “seeds” as separated as
possible
• Step 2 – cluster points to nearest seed
– Drift: As points are added, change seed
(centroid) to average of each coordinate
– Alternatively: Make full pass then recompute
seed and iterate.
• Step 3 – aggregate clusters using Ward’s
method
Clusters as Created
As Clustered – PROC FASTCLUS
Statistics to Data Mining Dictionary
Statistics
(nerdy)
Data Mining
(cool)
Independent variables
Dependent variable
Estimation
Clustering
Features
Target
Training, Supervised Learning
Unsupervised Learning
Prediction
Slopes, Betas
Intercept
Scoring
Weights (Neural nets)
Bias (Neural nets)
Composition of Hyperbolic
Tangent Functions
Radial Basis Function
and my personal
Type I and Type II Errors
Neural Network
Normal Density
favorite…
Confusion Matrix
Association Analysis
• Market basket analysis
– What they’re doing when they scan your “VIP”
card at the grocery
– People who buy diapers tend to also buy
_________ (beer?)
– Just a matter of accounting but with new
terminology (of course  )
Association Analysis is just elementary probability with new names
0.3
A
Pr{A
and B}
= 0.2
Pr{A} =0.5
Pr{B}
=0.3
A: Purchase Milk
B
B: Purchase Cereal
0.1
0.4
0.3+0.2+0.1+0.4 = 1.0
Cereal=> Milk
Rule B=> A “people who buy B will buy A”
Support:
Support= Pr{A and B} = 0.2
A
0.3
0.2
B
0.1
0.4
Independence means that Pr{A|B} = Pr{A} = 0.5
Pr{A} = 0.5 = Expected confidence if there is no
relation to B..
Confidence:
Confidence = Pr{A|B}=Pr{A and B}/Pr{B}=2/3
??- Is the confidence in B=>A the same as the
confidence in A=>B?? (yes, no)
Lift:
Lift = confidence / E{confidence} = (2/3) / (1/2) = 1.33
Gain = 33%
B
Marketing A to the 30%
of people who buy B will
result in 33% better sales
than marketing to a random
30% of the people.
TEXT MINING
Hypothetical collection of news releases (“corpus”) :
release 1: Did the NCAA investigate the basketball scores and
vote for sanctions?
release 2: Republicans voted for and Democrats voted against
it for the win.
(etc.)
Compute word counts:
NCAA basketball score vote Republican Democrat win
Release 1
1
1
1
1
0
0
0
Release 2
0
0
0
2
1
1
1
Text Mining Mini-Example: Word counts in 16 e-mails
--------------------------------words-----------------------------------------
d
o
c
u
m
e
n
t
E
l
e
c
t
i
o
n
P
r
e
s
i
d
e
n
t
1
2
3
4
5
6
7
8
9
10
11
12
13
14
20
5
0
8
0
10
2
4
26
19
2
16
14
1
8
6
2
9
0
6
3
1
13
22
0
19
17
0
R
e
p
u
b
l
i
c
a
n
B
a
s
k
e
t
b
a
l
l
D
e
m
o
c
r
a
t
V
o
t
e
r
s
N
C
A
A
10
9
0
7
4
9
1
4
9
10
0
21
12
4
12
5
14
0
16
5
13
16
2
11
14
0
0
21
6
4
0
12
0
5
0
2
16
9
1
13
20
3
0
2
2
14
0
19
1
4
20
12
3
9
19
6
1
0
12
2
15
5
12
9
6
0
12
0
0
9
L
i
a
r
T
o
u
r
n
a
m
e
n
t
S
p
e
e
c
h
5
9
0
12
2
20
13
0
24
14
0
16
12
3
3
0
16
3
17
0
20
12
4
10
16
4
5
8
8
12
4
15
3
18
0
9
30
22
12
12
9
0
W
i
n
s
S
c
o
r
e
_
V
S
c
o
r
e
_
N
18
12
24
22
9
13
0
3
9
3
17
0
6
3
15
9
19
8
0
9
1
0
10
1
23
0
1
10
21
0
30
2
1
14
6
0
14
0
8
2
4
20
Eigenvalues of the Correlation Matrix
1
2
3
4
5
6
7
8
9
10
11
12
13
Eigenvalue
Difference
7.10954264
2.30455155
1.00292318
0.76887967
0.55817886
0.45732963
0.30169451
0.16772870
0.16271459
0.1192580
0.0303509
0.0159719
0.0008758
4.80499109
1.30162837
0.23404351
0.21070080
0.10084923
0.15563511
0.13396581
0.00501411
0.04345658
0.08890707
0.01437903
0.01509610
Proportion
Cumulative
0.5469
0.1773
0.0771
0.0591
0.0429
0.0352
0.0232
0.0129
0.0125
0.0092
0.0023
0.0012
0.0001
Prin 2
Prin 1
0.5469
0.7242
0.8013
0.8605
0.9034
0.9386
0.9618
0.9747
0.9872
0.9964
0.9987
0.9999
1.0000
55% of the variation in
these 13-dimensional
vectors occurs in one
dimension.
Variable
Prin1
Basketball
NCAA
Tournament
Score_V
Score_N
Wins
-.320074
-.314093
-.277484
-.134625
-.120083
-.080110
Speech
Voters
Liar
Election
Republican
President
Democrat
0.273525
0.294129
0.309145
0.315647
0.318973
0.333439
0.336873
Eigenvalues of the Correlation Matrix
1
2
3
4
5
6
7
8
9
10
11
12
13
Eigenvalue
Difference
7.10954264
2.30455155
1.00292318
0.76887967
0.55817886
0.45732963
0.30169451
0.16772870
0.16271459
0.1192580
0.0303509
0.0159719
0.0008758
4.80499109
1.30162837
0.23404351
0.21070080
0.10084923
0.15563511
0.13396581
0.00501411
0.04345658
0.08890707
0.01437903
0.01509610
Proportion
0.5469
0.1773
0.0771
0.0591
0.0429
0.0352
0.0232
0.0129
0.0125
0.0092
0.0023
0.0012
0.0001
Cumulative
0.5469
0.7242
0.8013
0.8605
0.9034
0.9386
0.9618
0.9747
0.9872
0.9964
0.9987
0.9999
1.0000
Prin 2
Prin 1
Prin1 coordinate =
.707(word1) – .707(word2)
55% of the variation in
these 13-dimensional
vectors occurs in one
dimension.
Variable
Prin1
Basketball
NCAA
Tournament
Score_V
Score_N
Wins
-.320074
-.314093
-.277484
-.134625
-.120083
-.080110
Speech
Voters
Liar
Election
Republican
President
Democrat
0.273525
0.294129
0.309145
0.315647
0.318973
0.333439
0.336873
PROC CLUSTER (single linkage) agrees !
Cluster 2
Cluster 1
Summary
• Data mining – a set of fast stat methods for
large data sets
• Some new ideas, many old or extensions of old
• Some methods:
– Trees (recursive splitting)
– Logistic Regression
– Neural Networks
– Association Analysis
– Nearest Neighbor
– Clustering
– Etc.
Classification Variables (dummy variables, indicator variables)
Predicted Accidents = 1181 + 2579 X11
X11 is 1 in November, 0 elsewhere.
Interpretation:
In November, predict 1181+2579(1) = 3660.
In any other month predict 1181 + 2579(0) = 1181.
1181 is average of other months.
2579 is added November effect (vs. average of others)
Model for NC Crashes involving Deer:
Proc reg data=deer; model deer = X11;
Analysis of Variance
Source
Model
Error
Corrected Total
Root MSE
Variable
Intercept
X11
DF
1
58
59
580.42294
Label
Intercept
Sum of
Squares
30473250
19539666
50012916
R-Square
DF
1
1
Mean
Square
30473250
336891
F Value
90.45
Pr > F
<.0001
0.6093
Parameter
Estimate
1181.09091
2578.50909
Standard
Error
78.26421
271.11519
t Value
15.09
9.51
Pr > |t|
<.0001
<.0001
Looks like December and October need dummies too!
Proc reg data=deer; model deer = X10 X11 X12;
Analysis of Variance
Source
DF
Sum of
Squares
Mean
Square
Model
Error
Corrected Total
3
56
59
46152434
3860482
50012916
15384145
68937
Root MSE
Variable
Intercept
X10
X11
X12
262.55890
DF
1
1
1
1
Parameter
Estimate
929.40000
1391.20000
2830.20000
1377.40000
R-Square
Standard
Error
39.13997
123.77145
123.77145
123.77145
date
F Value
Pr > F
223.16
<.0001
0.9228
t Value
23.75
11.24
22.87
11.13
Pr > |t|
<.0001
<.0001
<.0001
<.0001
Average of Jan through Sept. is 929 crashes per month.
Add 1391 in October, 2830 in November, 1377 in December.
JAN03
FEB03
MAR03
APR03
MAY03
JUN03
JUL03
AUG03
SEP03
OCT03
NOV03
DEC03
JAN04
FEB04
MAR04
APR04
MAY04
JUN04
JUL04
AUG04
SEP04
OCT04
NOV04
DEC04
x10 x11 x12
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
1
What the heck – let’s do all but one (need “average of rest” so must leave out at least one)
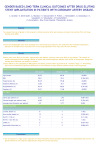
Proc reg data=deer; model deer = X1 X2 … X10 X11;
Analysis of Variance
Source
Model
Error
Corrected Total
Root MSE
DF
11
48
59
182.07290
Sum of
Squares
48421690
1591226
50012916
R-Square
Mean
Square
4401972
33151
F Value
132.79
Pr > F
<.0001
0.9682
Parameter Estimates
Variable
Label
Intercept
X1
X2
X3
X4
X5
X6
X7
X8
X9
X10
X11
Intercept
DF
Parameter
Estimate
Standard
Error
t Value
Pr > |t|
1
1
1
1
1
1
1
1
1
1
1
1
2306.80000
-885.80000
-1181.40000
-1220.20000
-1486.80000
-1526.80000
-1433.00000
-1559.20000
-1646.20000
-1457.20000
13.80000
1452.80000
81.42548
115.15301
115.15301
115.15301
115.15301
115.15301
115.15301
115.15301
115.15301
115.15301
115.15301
115.15301
28.33
-7.69
-10.26
-10.60
-12.91
-13.26
-12.44
-13.54
-14.30
-12.65
0.12
12.62
<.0001
<.0001
<.0001
<.0001
<.0001
<.0001
<.0001
<.0001
<.0001
<.0001
0.9051
<.0001
Average of rest is just December mean 2307. Subtract 886 in January,
add 1452 in November. October (X10) is not significantly different than
December.
positive
negative
Add date (days since Jan 1 1960 in SAS) to capture trend
Proc reg data=deer; model deer = date X1 X2 … X10 X11;
Analysis of Variance
Source
Model
Error
Corrected Total
Root MSE
DF
12
47
59
129.83992
Sum of
Squares
49220571
792345
50012916
R-Square
Mean
Square
4101714
16858
F Value
243.30
Pr > F
<.0001
0.9842
Parameter Estimates
Variable
Intercept
X1
X2
X3
X4
X5
X6
X7
X8
X9
X10
X11
date
Label
Intercept
DF
1
1
1
1
1
1
1
1
1
1
1
1
1
Parameter
Estimate
-1439.94000
-811.13686
-1113.66253
-1158.76265
-1432.28832
-1478.99057
-1392.11624
-1525.01849
-1618.94416
-1436.86982
27.42792
1459.50226
0.22341
Standard
Error
547.36656
82.83115
82.70543
82.60154
82.49890
82.41114
82.33246
82.26796
82.21337
82.17106
82.14183
82.12374
0.03245
t Value
-2.63
-9.79
-13.47
-14.03
-17.36
-17.95
-16.91
-18.54
-19.69
-17.49
0.33
17.77
6.88
Trend is 0.22 more accidents per day (1 per 5 days) and is significantly
different from 0.
Pr > |t|
0.0115
<.0001
<.0001
<.0001
<.0001
<.0001
<.0001
<.0001
<.0001
<.0001
0.7399
<.0001
<.0001
Receiver Operating Characteristic Curve
Cut point 1
Logits of 1s Logits of 0s
Logits
of 0s
red of 1s Logits
black
red
black
Receiver Operating Characteristic Curve
Cut point 2
Logits of 1s Logits of 0s
Logits
of 0s
red of 1s Logits
black
red
black
Receiver Operating Characteristic Curve
Cut point 3
Logits of 1s Logits of 0s
Logits
of 0s
red of 1s Logits
black
red
black
Receiver Operating Characteristic Curve
Cut point 3.5
Logits of 1s
red
Logits of 0s
black
Receiver Operating Characteristic Curve
Cut point 4
Logits of 1s
red
Logits of 0s
black
Receiver Operating Characteristic Curve
Cut point 5
Logits of 1s Logits of 0s
Logits
of 0s
red of 1s Logits
black
red
black
Receiver Operating Characteristic Curve
Cut point 6
Logits of 1s
red
Logits of 0s
black