* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download A New Gravitational Clustering Algorithm
Survey
Document related concepts
Transcript
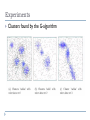
A New Gravitational Clustering Algorithm Jonatan Gomez, Dipankar Dasgupta, Olfa Nasraoui Outline Introduction Background Proposed Algorithm Analysis Introduction Many clustering techniques rely on the assumption that a data set follows a certain distribution and is free of noise Given noise, several techniques (k-means, fuzzy k-means) based on a least squares estimate are spoiled Most clustering algorithms require the number of clusters to be specified The authors propose a novel, robust, unsupervised clustering technique based on Newton’s Law of Gravitation, and Newton’s second law of motion Introduction Gravitational concepts have been applied to cluster visualization and analysis before Properties of Wright’s Gravitational Clustering [2]: New position of a particle is found using remaining particles When two particles are close they merge Maximum movement of particles per iteration is capped Algorithm terminates when only one particle remains Improvements over Wright: Speed, robustness, and determining number of clusters Background Newton’s Laws of Motion If acceleration is constant: Background Newton’s Law of Gravitation Background Optimal Disjoint Set Union-Find Structure A disjoint set Union-Find structure supports three operators: MAKESET(X) FIND(X) UNION(X,Y) Time complexity of any sequence of m Union and Find operations on n elements is at most O(m+n) in practice Proposed Algorithm Ideas behind applying gravitational law: A data point exerts a higher gravitational force on other data points in the same cluster than on data points not in the same cluster. Thus, points in a cluster move toward the center of the cluster. If a point is a noise point, the gravitational forces acting on it will be so small the point will be immobile. Thus, noise points won’t be assigned to any cluster Proposed Algorithm Simplified equation used to move point x according to gravitational field of point y Velocity considered to be zero at all points in time Reduce G after each iteration to prevent the “big crunch” Proposed Algorithm Proposed Algorithm Use threshold to extract valid clusters which have at least a minimum number of points Proposed Algorithm Similarities to Agglomerative Hierarchical Clustering Differences from Agglomerative Hierarchical Clustering Proposed Algorithm Comparison to Wright [2] Experiments Synthetic data Experiments Results (over 10 trials) Parameters: M = 500, G = 7x10-6, ∆G = 0.01, ε = 10-4 k-Means and Fuzzy k-Means given 150 iterations Experiments Clusters found by the G-algorithm Experiments Clusters found by the G-algorithm (noise removed) Experiments Movement of points over iterations Experiments Scalability (average of 50 trails for each percentage) Do not need to use entire data set to get good results Experiments Sensitivity to α Use α = 0.03 Experiments Sensitivity to G To big => one cluster To small => no clusters No universal value => depends on data set Experiments Sensitivity to ∆(G) To big => no clusters To small => one cluster Best value ~0.01 based on experiments Experiments Sensitivity to ε To big => one cluster Experiments Real data set Intrusion detection benchmark data set 42 attributes, 33 numerical, N = 492,021 2 classes – no intrusion (19.3%) and intrusion (80.7%) Use only the numerical attributes Use only 1% of the data (chosen randomly) Parameter settings G = 1x10-4 (based on testing) ∆(G) = 0.01 α = 0.03 ε = 1x10-6 M = 100 Experiments Clustering-Classification Strategy Assign to each cluster the class with more training data records assigned to that cluster Given an unknown data point, the data point is assigned to the closest cluster (the center of the clusters is used to compute the distance) Experiments Real data set results (over 100 trials) Conclusions / Future Work Successfully determines the number of clusters in noisy data sets Can be used to pre-process data by removing noise Three of four parameters can be set to constant values Future Work: Determine method to automatically set G Extend to different distance metrics References [1] J. Gomez, D. Dasgupta, and O. Nasraoui, “A New Gravitational Clustering Algorithm,” In Proc. of the SIAM Int. Conf. on Data Mining, 2003. [2] W. E. Wright, “Gravitational Clustering,” Pattern Recognition, 9:151166, Pergamon Press, 1977.