* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Snubber Circuits - aboutme.samexent.com
Valve RF amplifier wikipedia , lookup
Integrating ADC wikipedia , lookup
Regenerative circuit wikipedia , lookup
Flexible electronics wikipedia , lookup
Schmitt trigger wikipedia , lookup
Operational amplifier wikipedia , lookup
Index of electronics articles wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Integrated circuit wikipedia , lookup
Power electronics wikipedia , lookup
Power MOSFET wikipedia , lookup
Current mirror wikipedia , lookup
RLC circuit wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Crossbar switch wikipedia , lookup
Surge protector wikipedia , lookup
Network analysis (electrical circuits) wikipedia , lookup
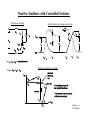
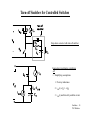
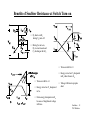
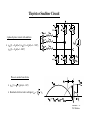
Lecture Notes Snubber Circuits William P. Robbins Dept. of Electrical and Computer Engineering University of Minnesota Outline A. Overview of Snubber Circuits B. Diode Snubbers C. Turn-off Snubbers D. Overvoltage Snubbers E. Turn-on Snubbers F. Thyristor Snubbers Snubbers -11 W.P. Robbins Overview of Snubber Circuits for Hard-Switched Converters Function: Protect semiconductor devices by: • Limiting device voltages during turn-off transients • Limiting device currents during turn-on transients • Limiting the rate-of-rise (di/dt) of currents through the semiconductor device at device turn-on • Limiting the rate-of-rise (dv/dt) of voltages across the semiconductor device at device turn-off • Shaping the switching trajectory of the device as it turns on/off Types of Snubber Circuits 1. Unpolarized series R-C snubbers • Used to protect diodes and thyristors 2. Polarized R-C snubbers • Used as turn-off snubbers to shape the turn-on switching trajectory of controlled switches. • Used as overvoltage snubbers to clamp voltages applied to controlled switches to safe values. • Limit dv/dt during device turn-off 3. Polarized L-R snubbers • Used as turn-on snubbers to shape the turn-off switching trajectory of controlled switches. • Limit di/dt during device turn-on Snubbers - 2 W.P. Robbins Need for Diode Snubber Circuit d i Df + Vd - Lσ Rs Df Cs Io i Df (t) Io Vd = d t Lσ t I rr Sw v • Lσ = stray inductance • S w closes at t = 0 • Rs - Cs = snubber circuit • Df (t) • Diode voltage without snubber t Vd Lσ di Lσ d t diLσ Diode breakdown if Vd + Lσ > BVBD dt Snubbers - 3 W.P. Robbins Equivalent Circuits for Diode Snubber Lσ + Vd - cathode Diode snap-off • Simplified snubber the capacitive snubber Rs Lσ anode + + v Cs - Vd i Df - t Cs • Rs = 0 • Worst case assumptiondiode snaps off instantaneously at end of diode recovery •v = -v Cs Df d2vCs Governing equation - • Boundary conditions - vCs(0+) = 0 and iLσ(0+) = Irr LσCs = Vd • dt2 + vCs LσCs Snubbers - 4 W.P. Robbins Performance of Capacitive Snubber • vCs(t) = Vd - Vd cos(ωot) + Vd • • Cbase sin(ωot) Cs ωo = 1 LσCs Vcs,max = Vd ; 1 + I 2 rr Cbase = Lσ Vd Cbase 1 + Cs 5 4 V Cs,max Vd 3 2 1 0 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 C base Cs 5 2 Snubbers - 5 W.P. Robbins Effect of Adding Snubber Resistance Snubber Equivalent Circuit Lσ i(t) - + V d - v Rs Df (t) + Cs • Governing equation • Boundary conditions i(0+) = Irr and Lσ d2i di i + Rs + =0 dt Cs dt2 Vd - IrrRs di(0+) = dt Lσ Diode voltage as a function of time Vdf Vd (t) = - 1 ωa = ωo e-αt sin(ωat - φ + ζ) ; Rs ≤ 2 Rb η cos(φ) Rs 2 1- (α/ ωo) ; α = 2 L ; ωo = σ 1 (2-x) η -1 ; φ = tan LσCs 4 - ηx2 Lσ [Irr]2 Cs Rs Vd η = C ; x = R ; Rb = I ; Cb = ; ζ = tan-1(α/ωa) 2 b b rr Vd Snubbers - 6 W.P. Robbins Performance of R-C Snubber 3 • • • • • At t = tm vDf(t) = Vmax tan-1(ωa/α) φ - ξ tm = + ω ≥0 ωa a Vmax Vd η = =1+ Cs Cbase Cbase = Ls Irr2 Vd2 x= and R V max V d 1 Rs Rbase Rbase = base = 1.3 2 1 + η-1 - x exp(-αtm) and R s,opt C s = Cbase R s I rr V d Vd Irr 0 0 1 Rs R base 2 Snubbers - 7 W.P. Robbins Diode Snubber Design Nomogram Wtot 2 L s I r r /2 3 WR 2 L s I r r /2 0 2 0 V max 0 0 0 V d 0 0 00 0 00 0 00 0 0 000 1 0 0 for R = R s s,opt 00 R s,op R base 0 0 1 C s / Cbase 2 3 8 Snubbers - 8 W.P. Robbins Need for Snubbers with Controlled Switches Step-down converter L1 V d L σ di dt L2 i L3 Switch current and voltage waveforms sw Sw Io i sw L σ di dt Io + vsw - I rr Io V d vsw to t • L1 , L 2 , L 3 = stray inductances • L σ = L1 + L 2 + L 3 t 1 t 4 3 t5 t6 Switching trajectory of switch idealized switching loci i sw t6 t5 turn-off to t1 turn-on t • Overvoltage at turn-off due to stray inductance • Overcurrent at turn-on due to diode reverse recovery 4 t3 Vd vsw Snubbers - 9 W.P. Robbins Turn-off Snubber for Controlled Switches i + V D f DF d Turn-off snubber Io Ds S - Rs w i Cs Io Df V Step-down converter with turn-off snubber Cs Equivalent circuit during switch turn -off. • Simplifying assumptions 1. No stray inductance. d Io - i i sw Cs sw 2. isw(t) = Io(1 - t/tfi) 3. isw(t) uneffected by snubber circuit. Snubbers - 10 W.P. Robbins Turn-off Snubber Operation • • I ot I ot Capacitor voltage and current for 0 < t < tfi iCs(t) = tfi 2 and v (t) = Cs 2C t s fi Iotfi For Cs = Cs1, vCs = Vd at t = tfi yielding Cs1 = 2Vd Circuit waveforms for varying values of Cs i i sw i sw sw Io i i Df tf i i i Df Df t tf i fi Cs V d v Cs Cs < Cs 1 Cs = Cs 1 Cs > C s 1 Snubbers - 11 W.P. Robbins Benefits of Snubber Resistance at Switch Turn-on vs w D Io f • Ds shorts out Rs during Sw turn-off. Rs V d Sw t rr Io i • During Sw turn-on, Ds reverse-biased and Cs discharges thru Rs. Ds Cs D I rr f Vd Io i sw Rs I rr • Turn-on with Rs > 0 discharge of C s t rr • Turn-on with Rs = 0 vs w V i sw Io d t ri 0 • Energy stored on Cs dissipated in Rs rather than in Sw. t t ri + t rr 2 • Energy stored on Cs dissipated in Sw. • Extra energy dissipation in Sw because of lengthened voltage fall time. • Voltage fall time kept quite short. Snubbers - 12 W.P. Robbins Effect of Turn-off Snubber Capacitance 1 Energy dissipation W / total Wbase W 0.8 WR = dissipation in resistor 0.6 W / Wbase R 0.4 WT / W base W 0.2 0 WT = dissipation in switch Sw 0 0.2 0.4 0.6 0.8 1 1.2 Iotfi Cs1 = 2Vd 1.4 Wtotal = WR + WT Cs / Cs1 i Wbase = 0.5 VdIotfi sw Io Cs < Cs1 RBSOA Switching trajectory Cs = Cs1 Cs > Cs1 V d vs w Snubbers - 13 W.P. Robbins Turn-off Snubber Design Procedure Selection of Cs • Minimize energy dissipation (WT) in BJT at turn-on • Minimize WR + WT • Keep switching locus within RBSOA Snubber recovery time (BJT in on-state) • Reasonable value is Cs = Cs1 • Capacitor voltage = Vd exp(-t/RsCs) • Time for vCs to drop to 0.1Vd is 2.3 RsCs • BJT must remain on for a time of 2.3 RsCs Selection of Rs Vd • Limit icap(0+) = R < Irr s • Usually designer specifies Irr < 0.2 Io so Vd Rs = 0.2 Io Snubbers - 14 W.P. Robbins Overvoltage Snubber Lσ + D f Io R i ov Vd - kV d s w Io Sw Dov C ov • Step-down converter with overvoltage snubber comprised of Dov, Cov, and Rov. • Overvoltage snubber limits overvoltage (due to stray Inductance) across Sw as it turns off. v V d s w o t fi • Switch Sw waveforms without overvoltage snubber • tfi = switch current fall time ; kVd = overvoltage on Sw diLσ Io • kVd = Lσ = Lσ dt tfi kVdtfi • Lσ = Io Snubbers - 15 W.P. Robbins Operation of Overvoltage Snubber i + • Dov on for 0 < t < Lσ L σ V d - R Dov C ov • tfi << π π LσCov 2 LσCov 2 + ov v - Cov • Dov,Cov provide alternate path for inductor current as Sw turns off. • Switch current can fall to zero much faster than Ls current. • Df forced to be on (approximating a short ckt) by Io after Swis off. Snubbers - 16 W.P. Robbins Overvoltage Snubber Design • Limit vsw,max to 0.1Vd kVd tfi Io • Using L = • Cov = kVdtfiIo2 Io(0.1Vd)2 = Io Lο Cov in above equation yields € = 100k tfi Io Vd • Cov = 200 k Cs1 where Cs1 = tfiIo 2Vd which is used in turn-off snubber • Choose Rov so that the transient recovery of Cov is critically damped so that ringing is minimized. For a critically damped circuit Q = 1 = • € Rov = ω o Lσ = Rov Lσ 1 C ov Rov . 0.1Vd Io • Check€that the recovery time of Cov (2.3L /Rov) is less than off-time duration, toff, of the switch Sw. • With choice of Rov from above, trecovery is trecovery = 23 k tf i Snubbers - 17 W.P. Robbins Turn-on Snubber + D I f V d Ls o + f Snubber circuit Ls D R Ls D V d Ls Sw - Io R D Step-down converter with turn-on snubber D Ls Io Ls f Sw - • Snubber reduces Vsw at switch turn-on due drop across inductor Ls. • Will limit rate-of-rise of switch current if Ls is sufficiently large. i sw With snubber Without snubber Switching trajectory with and without turn-on snubber. Ls di sw dt v V d sw Snubbers - 18 W.P. Robbins Turn-on Snubber Operating Waveforms v Small values of snubber inductance (Ls < Ls1) • disw controlled by switch Sw dt and drive circuit. • Δvsw = V tri i Io s w v disw Vd Io • limited by circuit to < dt Ls tri • d LsIo Large values of snubber inductance (Ls > Ls1) • Ls1 = I rr s w t ri t rr I rr s w reduced V d Io Vdtri Io Irr reduced when Ls > Ls1 because Irr proportional to i disw dt s w t on ≈ Ls Io V d > ri t rr+ t Snubbers - 19 W.P. Robbins Turn-on Snubber Recovery at Switch Turn-off + D Io f I o R Lsexp(-R Lst/L s ) Io R Ls is w V d - Ls R Ls D Ls vs w V d Io t rv Sw • Switch waveforms at turn-off with turn-on snubber in circuit. • Assume switch current fall time tri = 0. • Inductor current must discharge thru DLs- RLs series segment. • Overvoltage smaller if tfi smaller. • Time of 2.3 Ls/RLs required for inductor current to decay to 0.1 Io • Off-time of switch must be > 2.3 Ls/RLs Snubbers - 20 W.P. Robbins Turn-on Snubber Design Trade-offs Selection of inductor • Larger Ls decreases energy dissipation in switch at turn-on • Wsw = WB (1 + Irr/Io)2 [1 - Ls/Ls1] • WB = VdIotfi/2 and Ls1 = Vdtfi/Io • Ls > Ls1 Wsw = 0 • Larger Ls increases energy dissipation in RLs • WR = WB Ls / Ls1 • Ls > Ls1 reduces magnitude of reverse recovery current Irr • Inductor must carry current Io when switch is on - makes inductor expensive and hence turn-on snubber seldom used Selection of resistor RLs • Smaller values of RLs reduce switch overvoltage Io RLs at turn-off • Limiting overvoltage to 0.1Vd yields RLs = 0.1 Vd/Io • Larger values of RLs shortens minimum switch off-time of 2.3 Ls/RLs Snubbers - 21 W.P. Robbins Thyristor Snubber Circuit P 3-phase thyristor circuit with snubbers • van(t) = Vssin(ωt), vbn(t) = Vssin(ωt - 120°), vcn(t) = Vssin(ωt - 240°) 1 van + Lσ - vbn + Lσ v cn + Lσ - 5 3 A B - i d C Cs 6 4 2 Rs Phase-to-neutral waveforms • vLL(t) = v 3 Vssin(ωt - 60°) • Maximum rms line-to-line voltage VLL = v α an bn 3 V 2 s v LL = v bn v an= v ba ω t 1 Snubbers - 22 W.P. Robbins Equivalent Circuit for SCR Snubber Calculations Assumptions • Trigger angle α = 90° so that vLL(t) = maximum = 2 VLL Equivalent circuit after T1 reverse recovery • Reverse recovery time trr << period of ac waveform so that vLL(t) equals a constant value of vba(ωt1) = • Worst case stray inductance Lσ gives rise to reactance equal to or less than 5% of line impedance. • Line impedance = Vs 2Ia1 = 2VLL 6Ia1 = i 2 VLL VLL 3Ia1 + V (ω t1) ba - where Ia1 = rms value of fundamental component of the line current. VLL • ωLσ = 0.05 3Ia1 2 Lσ Lσ P Cs T1 after recovery T 3 (on) i T1 Rs A Snubbers - 23 W.P. Robbins Component Values for Thyristor Snubber • • Use same design as for diode snubber but adapt the formulas to the thyristor circuit notation Snubber capacitor Cs = Cbase = Lσ I 2 rr Vd diLσ dt • From snubber equivalent circuit 2 Lσ • Irr = • Vd = • Cs = Cbase = • Snubber resistance Rs = 1.3 Rbase = 1.3 • • diLσ trr dt 2VLL = trr = 2Lσ = 2VLL 0.05 VLL 2 3 Ia1ω 2 VLL trr = 25 ωIa1trr 2 VLL Rs = 0.05 VLL 3 Ia1ω 1.3 25 ωI 2 a1trr = 2VLL 2VLL 25ωIa1trr = 8.7 ωIa1trr VLL Vd Irr 0.07 VLL ωIa1trr Energy dissipated per cycle in snubber resistance = WR • WR = LσIrr2 2 + CsVd2 2 = 18 ω Ia1 VLL(trr)2 Snubbers - 24 W.P. Robbins