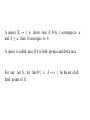Download On D - completions of some *topological structures*

Three levels of D - completions
Zhao Dongsheng
Ho Weng Kin, Wee Wen Shih
Mathematics and Mathematics Education
National Institute of Education,
Nayang Technological University,
Singapore
The 2nd International Conference on Quantitative Logic and Soft
Computing
22-25, October, 2010
Jimei University, Xiamen , China
Outline:
• Subcategory and reflectivity
• Posets , dcpo’s and D – completion of posets
• Monotone convergence ( d - ) spaces,
d-completion of T0 - spaces
• Convergence spaces, D-completion
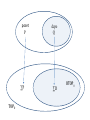
1. Subcategory and reflectivity
Given a category C and a subcategory E of C, E is
reflective in C if the inclusion functor from E into C
has a left adjoint.
ηX
G(X)
X

f
f
C
E
Y
Stone–Čech
compactification
Examples
X
βX
KHSP
CRSP
soberification
X
SX
Sober
TOP0
A space Y is sober if for any non-empty
irreducible closed set F of Y, there is a unique
element a in Y such that F = cl({a})
2. Directed complete posets and dcpo-completion
A non-empty subset D of a poset (P, ≤ ) is directed
if any two elements in D has an upper bound in D.
A poset (P, ≤ ) is directed complete if every directed
subset D of P has a supremum (join) sup D.
A directed complete poset is also called a dcpo.
A mapping f : P → Q between two posets is
Scott continuous if it preserves joins of directed sets:
f( sup D)=sup f(D)
for every directed D for which sup D exists.
Let POS ( DCPO) be the category of posets ( dcpo ) and Scott
continuous mappings between posets.
Question:
Is DCPO reflective in POS ?
Definition [11]
The D-completion of a poset P is a dcpo D(P) ,
together with a Scott continuous mapping η : P → D(P)
such that for any Scott continuous f: P → Q into a dcpo
Q, there is a unique Scott continuous g: D(P) → Q such
that f= g○η
A subset U of P is Scott open if the following
conditions are satisfied:
(i) U=↑U ;
(ii) for any directed set D, sup D in U implies D∩U is nonempty
The set of all Scott closed (open ) sets of P is denoted
by Г(P) ( σ(P)), which is a complete lattice under the
inclusion relation.
A subset F of a poset P is called D-closed if for any
directed subset, D  F implies sup D  F whenever
sup D exists.
The D – closed sets defines a topology--- D - topology.
* A subset F is Scott closed iff it is a down set and
D-closed
Theorem [11]
For every poset P, the D - closure of ф={↓x: x is in P}
in Г(P), or the smallest subdcpo containing ф, is the
D-completion of P.
Theorem[11]
(1) P is continuous iff D(P) is continuous.
(2) P is algebraic iff P is algebraic.
(3) Г(P)≡ Г(D(P)).
*The directed completion o f continuous posets was
considered in [10].
* The dcpo – completion of posets was also considered in
[6] and [7] with different motivations.
* The local dcpo –completion was first considered in
[8] and was revised in [11]
For any T0 space X, the specialization order  on
X is defined as :
x  y iff x is in cl({y}).
3. d-spaces and d-completion to topological
spaces
Remark
1. For any poset P, ΣP=(P, σ(P)) is a T0 space. The
specialization order is the original order on P.
2. f: P → Q is Scott continuous iff it is continuous with
respect to the Scott topology.
So the category POSd is a full subcategory of TOP0
3. If P is a dcpo, then
(i) the specialization of ΣP is directed complete, and
(ii) for any directed subset D, D converges to sup D,
as a net.
Definition
A topological space X satisfying (i) and (ii) is called a
d - space, or monotone convergence space.
Remark:
1. For any poset P, the Scott space ΣP is a d-space iff P is
directed complete.
2. Every Sober space is a d-space.
2. If X is a d - space, then every open set U of X is a
Scott open set of (X, ≤ ), where is the specialization
order on X.
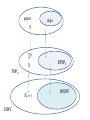
poset
P
∑P
TOP0
dcpo
Q
∑D
DTOP0
Question:
Is DTOP reflexive in TOP0?
Theorem [9] [1] [7]
For each T0 space X there is a d –space D(X) and a
continuous mapping η : X → D(X) such that for any
continuous f: X → Y into a d-space Y, there is a unique
Scott continuous g: D(X) → Y such that f= g∙η .
Theorem [7
For any poset, the d-completion D( ∑P) of the space ∑P
with the specialization order is the D-completion of P.
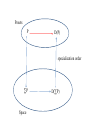
Posets
P
D(P)
specialization order
∑P
Space
D(∑P)
So the D – completion of topological spaces is a
generalization of D – completion of posets
4. Net convergence spaces and D-completion
Definition [ 5]
A (net ) convergence space is a pair (X, →), where X is a
non-empty set and → is a collection of pairs ( S, x ) with S
a net in X and x an element in X ( we write S→x if
(S, x) belongs to → and say that S converges to x ),
such that the following conditions are satisfied:
1.( CONSTANT NET) For any x in X, {x}→x.
2. ( SUBNET) If S → x then S1 → x for any subnet S1 of S.
Continuous functions between convergence spaces are
defined in the usual way. Let CONV be the category
of convergence spaces and continuous functions
between them.
* A net S=(xi ) is a subnet of T=(yj ) if for any j0 there
is i0 such that for any i0 ≤ i , xi belongs to the
j0 - tail of T.
* CONV is cartesian closed
Example
Every topological space (X, τ ) defines convergence space
(X,  ) in the ordinary sense. Such a convergence
space is called a topological convergence space.
Also the assignment of (X,  ) to (X, τ ) extends to
a functor from TOP to CONV, setting TOP as a full
subcategory of CONV.
Definition :
A subset U of a convergence space ( X, → ) is open if
S=(xi ) → x and x is in U, then xi is in U eventually.
The set of all open sets U of ( X, → ) form a topology ,
called the
induced topology and denoted by  .
The specialization order ≤ of the topological space (X,  )
is called the specialization order of ( X, → ) .
A space ( X, → ) is up – nice if S=(xi ) converges to a
and T=(yj ) is a net satisfying the condition below , then T
converges to a:
for any i0 there is j0 such that for any j0 ≤ j , yj
belongs to
↑{xi : i0 ≤ i }.
A space ( X, → ) is down– nice if S=(xi ) converges to a
and b ≤ a , then S converges to b .
A space is called nice, if it is both up-nice and down nice.
For any net S , let lim S={ x: S → x } be the set of all
limit points of S.
Definition[5]
A convergence space ( X, →) is called a d - space of
1). It is order – nice;
2). For any directed set D={ xi : i in I }, sup D exists
and
D → sup D ( take D as a net ).
3). For any net, lim S is closed under supremum of
directed sets.
Example[5]
For each poset P, define → by:
S=(xi ) → x if there is a directed set E
with sup E exist,
x ≤ sup E , and for any e in E,
e≤ xi eventually.
Then
(i) (P, ≤ ) is order – nice;
(ii) (P, ≤ ) is a d – space iff P is a dcpo;
(iii) (P, ≤ ) is topological iff P is a continuous
poset .
Example A topological space (X, τ ) is a d- space iff
the convergence space (X,  ) is a d – space.
Theorem
The category DCONV of d- convergence spaces
( as a subcategory of CONV) is Cartesian closed
Definition
A space ( X, → ) is called an IL space if it satisfies
the Iterated Limit Axiom.
Remark
(1) For any poset P, ( P, →d ) is an IL space if it is
topological, iff P is continuous.
(2) Every topological convergence space is IL.
Definition[5]
A D – completion of a space ( X, → ) is d – space Y
together with a continuous map η : X →Y, such that
for any continuous f: X → Z from X into a d – space
Z, there is a unique continuous h: Y → Z such that
f=h ○η.
Theorem [5]
If X can be embedded into an IL d-space, then X
has a d – completion.
Corollary
Every T0 topological spaces has a d – completion
which is also topological.
poset
dcpo
P
∑P
X
DTOP0
TOP0
(X, )
CONV
DCONV
Problem:
Does every convergence space have a d – completion?
References
[1] Erchov, Yu. L.: On d-spaces, Theoretical Computer Science, (1999),
224: 59-72.
[2] Gierz, G. et al.: Continuous lattices and Domains,
Encyclopedia of Mathematics and Its Applications, Vol.93.
[3] R. Heckmann: A non- topological view of dcpos as convergence
spaces. Theoretical Computer Science, 305(1193), 195 -186.
[4] W. Ho, and D. Zhao, Lattices of Scott-closed sets,
Comment. Math. Univer. Carolinae, 50(2009), 2:297-314.
[5] W. Ho, D. Zhao and W. Wee,
d – completion of net convergence space, Proceeding of this conference.
[6] A. Jung, M. A. Moshier and S. Vickers,
Presenting dcpos and dcpo algebras, (Preprint).
[7] Keimel, K. and Lawson, J. D.: D-completions and the d-topology, Annals of
Pure and Applied Logic 59(2009), 3:292-306.
[8] M. W. Mislove, Local DCPOs, Local CPOs and Local
completions, Electronic Notes in Theoretical Computer Science ,
20(1999).
[9] Wyler, O.: Dedekind complete posets and Scott topologies, In: Lecture
Notes In Mathematics, Springer-Verlag, 1981.
[10] L. Xu, Continuity of posets via Scott topology and sobrification,
Topology Appl., 153(2006), 11:1886-1894.
[11] Zhao, D. and Fan, T., dcpo-completion of posets, Theoretical Computer
Science, 411(2010), 2167-2173.
Thank you !