Download Black Body Radiation and Wien`s Law File

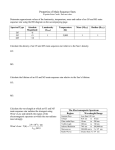
THERMAL RADIATION
And the Planck Distribution
Star Colours
When we look at the stars on a dark night
we can quite easily see that stars are
coloured.
This is an effect produced by the surface
temperature of a star.
Radiating Heat
• Standard bodies are black
• Measure the radiation given off by a black
body at every frequency of the spectrum at
a fixed temperature
Changing the temperature
• Think of a black cooker hot plate.
• It does not remain black but glows when
heated
Getting Hotter
Intensity W/m2
12000
K
6000 K
3000 K
Wavelength (m)
Intensity W/m2
λmax
Wavelength (m)
Intensity W/m2
Wavelength (m)
The Properties Of The Curves
1. the curve is flatter for lower temperature
2. As the temperature increases the wavelength of
maximum intensity (λmax) for that temperature
increases in promenance
3. As the temperature increases λmax moves to the left
towards higher frequency.
4. At higher temperatures there is a sharp falling off of
radiation at values greater than λmax towards a
limiting value in the ultraviolet range which is of very
short wavelength but not zero. This is referred to as
the ultra violet catastrophe.
Intensity W/m2
In 1893 Wihelm Wien dicovered a simple
relationship between λmax and the absolute
temperature of a body
Ultraviolet
Catastrophe
λmaxT = 2.898 x 10-3
Wavelength (m)
As the temperature of the star rises the λmax moves more towards the violet
Using Wien’s Law
λmaxT = 2.898 x 10-3
The spectrum of star  Andromedae is found to be at maximum
intensity at a wavelength of 380 nanometres.
a) What is the surface temperature of the star.
b) What colour would you expect this star to be?
λmaxT = 2.898 x 10-3
Intensity W/m2
T
2.898 10 3
max
2.898 10 3
T
380 10 9
T=7626K
λmax = 380 x10-9m
Wavelength (m)
As the star’s maximum wavelength is beyond the violet end of the spectrum
most of the visible light produced will be blue. It is a blue star.
• Work out the surface
temperature of each
of the star’s here
using Wien's law
• Suggest the observed
colour of each star
star
wavelength of
maximum
intensity(nm)
α draconis
430
ε Ursa Minoris
520
 cephei
740