Download Chapter 11 Frequency Response

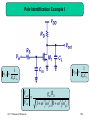
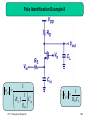
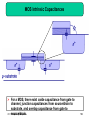
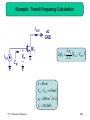
Chapter 11 Frequency Response









11.1
11.2
11.3
11.4
11.5
11.6
11.7
11.8
11.9
Fundamental Concepts
High-Frequency Models of Transistors
Analysis Procedure
Frequency Response of CE and CS Stages
Frequency Response of CB and CG Stages
Frequency Response of Followers
Frequency Response of Cascode Stage
Frequency Response of Differential Pairs
Additional Examples
1
Chapter Outline
CH 11 Frequency Response
2
High Frequency Roll-off of Amplifier
 As frequency of operation increases, the gain of amplifier
decreases. This chapter analyzes this problem.
CH 11 Frequency Response
3
Example: Human Voice I
Natural Voice
Telephone System
 Natural human voice spans a frequency range from 20Hz to
20KHz, however conventional telephone system passes
frequencies from 400Hz to 3.5KHz. Therefore phone
CH 11conversation
Frequency Response differs from face-to-face conversation.
4
Example: Human Voice II
Path traveled by the human voice to the voice recorder
Mouth
Air
Recorder
Path traveled by the human voice to the human ear
Mouth
Air
Ear
Skull
 Since the paths are different, the results will also be
different.
CH 11 Frequency Response
5
Example: Video Signal
High Bandwidth
Low Bandwidth
 Video signals without sufficient bandwidth become fuzzy as
they fail to abruptly change the contrast of pictures from
complete white into complete black.
CH 11 Frequency Response
6
Gain Roll-off: Simple Low-pass Filter
 In this simple example, as frequency increases the
impedance of C1 decreases and the voltage divider consists
of C1 and R1 attenuates Vin to a greater extent at the output.
CH 11 Frequency Response
7
Gain Roll-off: Common Source
Vout

1 
  g mVin  RD ||

C
s
L 

 The capacitive load, CL, is the culprit for gain roll-off since
at high frequency, it will “steal” away some signal current
and shunt it to ground.
CH 11 Frequency Response
8
Frequency Response of the CS Stage
Vout

Vin
g m RD
RD2 C L2 2  1
 At low frequency, the capacitor is effectively open and the
gain is flat. As frequency increases, the capacitor tends to
a short and the gain starts to decrease. A special
is ω=1/(RDCL), where the gain drops by 3dB.
CH 11frequency
Frequency Response
9
Example: Relationship between Frequency
Response and Step Response
H  s  j  
1
R12C12 2  1

t 
Vout  t   V0 1  exp
 u t 
R1C1 

 The relationship is such that as R1C1 increases, the
bandwidth drops and the step response becomes slower.
CH 11 Frequency Response
10
Bode Plot

s 
s 
1 
1 
 
 z1   z 2 

H ( s )  A0



s
s
1 
1 

    
p1 
p2 

 When we hit a zero, ωzj, the Bode magnitude rises with a
slope of +20dB/dec.
 When we hit a pole, ωpj, the Bode magnitude falls with a
ofResponse
-20dB/dec
CH 11slope
Frequency
11
Example: Bode Plot
 p1
1

RD C L
 The circuit only has one pole (no zero) at 1/(R DCL), so the
slope drops from 0 to -20dB/dec as we pass ωp1.
CH 11 Frequency Response
12
Pole Identification Example I
 p1
 p2 
1

RS Cin
Vout

Vin
CH 11 Frequency Response
1  
1
RD C L
g m RD
2
 p21 1   2  p2 2 
13
Pole Identification Example II
 p1
1


1 
 RS ||
Cin
gm 

CH 11 Frequency Response
 p2
1

RD C L
14
High-Pass Filter Response
Vout

Vin
R1C1
R12C1212  1
 The voltage division between a resistor and a capacitor can
be configured such that the gain at low frequency is
reduced.
CH 11 Frequency Response
15
Example: Audio Amplifier
Ci  79.6nF
CL  39.8nF
Ri  100 K
g m  1 / 200
 In order to successfully pass audio band frequencies (20
Hz-20 KHz), large input and output capacitances are
needed.
CH 11 Frequency Response
16
Capacitive Coupling vs. Direct Coupling
Capacitive Coupling
Direct Coupling
 Capacitive coupling, also known as AC coupling, passes
AC signals from Y to X while blocking DC contents.
 This technique allows independent bias conditions between
Direct coupling does not.
CH 11stages.
Frequency Response
17
Typical Frequency Response
Lower Corner
CH 11 Frequency Response
Upper Corner
18
MOS Intrinsic Capacitances
 For a MOS, there exist oxide capacitance from gate to
channel, junction capacitances from source/drain to
substrate, and overlap capacitance from gate to
CH 11source/drain.
Frequency Response
19
Gate Oxide Capacitance Partition and Full Model
 The gate oxide capacitance is often partitioned between
source and drain. In saturation, C2 ~ Cgate, and C1 ~ 0. They
are in parallel with the overlap capacitance to form CGS and
CGD.
CH 11 Frequency Response
20
Transit Frequency
gm
2f T 
CGS
gm
2f T 
C
 Transit frequency, fT, is defined as the frequency where the
current gain from input to output drops to 1.
CH 11 Frequency Response
21
Example: Transit Frequency Calculation
3 n
VGS  VTH 
2fT 
2
2L
L  65nm
VGS  VTH  100mV
 n  400cm 2 /(V .s )
fT  226GHz
CH 11 Frequency Response
22