Download Intermolecular interactions

Intermolecular interactions János Ángyán Équipe Modélisaton Quantique et Cristallographique, LCM3B – 2008 – J. Ángyán (EMQC) IMF 1 / 201 Part I Introduction J. Ángyán (EMQC) IMF 2 / 201 What are intermolecular forces? N2 crystal why are the N2 molecules arranged this way? what are the optimal intermolecular distances? what is the physical origin of the interactions that govern the structure? Intermolecular interactions fragments (subsystems) are well-defined and preserve their identity usually between closed shell molecules, ions or atoms much weaker than chemical bonding long range J. Ángyán (EMQC) IMF 3 / 201 Why are intermolecular forces interesting? Intermolecular forces play an important rôle in numerous fields Deviations of gases from ideal behaviour (pressure, viscosity, diffusion, thermal conductivity). Existence of condensed phases matter Properties of solids and liquids e.g. melting and boiling points. Organization of matter solids, crystal structures Polymorphism requires a very accurate knowledge of intermolecular forces. Liquid structure (pair distribution function, etc.) Reaction mechanisms (steric effects, Organization of soft matter, biopolymers. Heterogeneous catalysis Formation of surface monolayers, micelles and membranes, Transport of ions and molecules across biological membranes Atmospheric chemistry, etc... J. Ángyán (EMQC) IMF 4 / 201 Gecko feet adhesion by van der Waals forces Autumn et al. Proc. Natl. Acad. Sci. 99 (2002) 122. J. Ángyán (EMQC) IMF 5 / 201 Intermolecular potential Ar2 dimer Interaction-dependent contribution, U (R),the interaction energy or intermolecular pair-potential U (R) = Etot (R) − Etot (∞) = Etot (R) − EA − EB The intermolecular pair-potential is the work to bring together the two systems from infinity to the distance R, against the intermolecular force, F (R) Z ∞ U (R) = F (r)dr At infinitely large distance, there is no interaction: the energy is the sum of the energy of isolated atoms Etot (∞) = EA + EB R where At an arbitrary, finite R distance, the total energy F (R) = − Etot (R) = EA + EB + U (R) J. Ángyán (EMQC) IMF dU dEtot =− dR dR 6 / 201 Potential and force U(R) σ is the hard core radius σ Rm ε is the well depth −ε repulsive for R < Rm F(R) attractive for R > Rm Rm for σ < R < Rm negative, but repulsive R Intermolecular energy can negative, but the interaction is repulsive (F>0). J. Ángyán (EMQC) IMF 7 / 201 General intermolecular potential For polyatomic subsystems the intermolecular interaction energy U (R, ω; q A , q B ) depends on the relative position and orientation {R, ω} and on the internal coordinates {q A , q B } R: intermolecular vector (in polar coordinates) ω: relative Euler-angles Even if we neglect the intramolecular degrees of freedom, {q A , q B }, the intermolecular PES (potential energy surface) is six-dimensional. J. Ángyán (EMQC) IMF 8 / 201 Cluster expansion of the interaction energy The interaction energy can be decomposed to the sum of one-, two-, three-, etc. body contributions X 1X 1 X 1 X UN = Ui + Uij + Uijk + Uijkl + . . . 2 ij 3! 4! i ijk ijkl one-body: geometrical deformation of the monomers two-body: dominating term (additivity) three-body, four-body, etc. (non-additivity) Effective (system-dependent) pair-potential UN = X Ui + i 1 X eff Uij (N ) 2 ij may be quite different from the pure pair-potential. Attention: an effective pair-potential, usually obtained by fitting condensed-phase experimental data, is usually not valid for simple binary complexes. J. Ángyán (EMQC) IMF 9 / 201 U(R) Interaction ranges Range Subsystems Overlap Description short intermediate long easy to identify difficult quite easy strong weak no SM SM/PT PT R J. Ángyán (EMQC) IMF 10 / 201 Calculation of intermolecular interaction energy ĤAB = ĤA + ĤA + λV̂AB Supermolecule approach Perturbation theory U = ∆E = U = ∆E = E(AB) − E(A) − E(B) ∞ X λn ∆E (n) n=1 difference of the total energies (large numbers) directly, from the power series expansion in the strength of interaction technically very simple leads directly to the interaction energy does not depend on the intensity of the interaction based on the monomer wavefunction/properties difficult to interpret in terms of the monomer properties easy to interpret (physical insight, decomposition) energy components may have large errors with respect to the interaction energy provides basis of approximate analytical energy expressions systematic errors (BSSE) is the expansion convergent? J. Ángyán (EMQC) IMF 11 / 201 Water molecule density Electron density isosurface at 0.05 e/Å3 J. Ángyán (EMQC) IMF 12 / 201 Water molecule electrostatic potential Electrostatic potential isosurfaces at ±0.1 e/Å3 J. Ángyán (EMQC) IMF 13 / 201 Change of electron density under field Fz =0.028 a.u.; electron density isosurface at ±0.05 e/Å3 J. Ángyán (EMQC) IMF 14 / 201 Change of electron density under field Fz = 0.028 a.u.; deformation density isosurfaces at ±0.001 e/Å3 J. Ángyán (EMQC) IMF 15 / 201 Change of electrostatic potential under field Fz = 0.028 a.u.; potential difference isosurface at ±0.01 e/Å3 J. Ángyán (EMQC) IMF 16 / 201 Long-range correlation effect on the density He dimer: attractive London dispersion forces are due to tiny charge density rearrangements, predicted by Feynmann in 1939. J. Ángyán (EMQC) IMF 17 / 201 Short range antisymmetry effect on the density He dimer deformation density δ%(r) = %He2 (r) − %Hea (r) − %Heb (r) At short distances electrons density is depleted between the two closed shell atom consequence of the Pauli principle. J. Ángyán (EMQC) IMF 18 / 201 Main contributions to the interaction energy Contribution Long-range (U ∼ R−n ) Electrostatic Induction Dispersion Short-range (U ∼ e−αR ) Penetration Overlap repulsion Damping Charge transfer J. Ángyán (EMQC) Pairwise Additive? Sign Comment Yes No approx. ± − − Strong orientation dependence Strongly non-additive Always present Yes No approx. No − + + − Can be repulsive at very short range Dominates at very short range Antisym. effect on induction and disp. Donor-acceptor interaction IMF 19 / 201 Part II Experimental sources J. Ángyán (EMQC) IMF 20 / 201 Experimental sources of intermolecular forces crystal structure analysis thermodynamical properties: heat of vaporization (Trouton’s rule) crystal structures ionic crystals rare gas solids physico-chemical properties: bulk modulus, phonon spectrum, etc. virial coefficients of real gases viscosity, thermal conductivity (collision integrals) spectroscopy: VRT (vibration-rotation tunneling) J. Ángyán (EMQC) IMF 21 / 201 Theory vs. experiments EXPERIMENT {Dexp} {Dtheor} model model Uexp Utheor QUANTUM CHEMISTRY J. Ángyán (EMQC) IMF 22 / 201 Crystal structure analysis van de Waals radii (Pauling, Bondi) anisotropy of the interactions properties of the hydrogen bond J. Ángyán (EMQC) IMF 23 / 201 Interacting atoms are often aspheric Pauling and Bondi compiled nonbonded interatomic distances from crystal structures: tables of spherical van der Waals radii. Atom F Cl Br I N O S Se Bondi 1.47 1.76 1.85 1.98 1.70 1.50 1.74 2.00 rmax 1.38 1.78 1.84 2.13 1.60 1.54 2.03 2.15 rmin 1.30 1.58 1.54 1.76 1.60 1.54 1.60 1.70 Bondi’s vdW radii and major and minor anisotropic radii proposed by Nyburg and Faerman. Nyburg and Faerman, Acta Cryst. B. 41 (1985) 274 J. Ángyán (EMQC) IMF 24 / 201 Anisotropic Cl· · · Cl contacts S.L. Price et al. , J.A.C.S. 116 (1994) 4910 J. Ángyán (EMQC) IMF 25 / 201 Trouton’s rule Empirical relationship between enthalpy of vaporization, ∆Hvap and boiling point, Tb at atmospheric pressure ∆Hvap ≈ 10RTb = 85J K−1 mol−1 Can be explained by the fact that the change in Gibbs free energy is zero at the boiling point, Tb , ∆Gvap = 0 ∆Hvap = Tb ∆Svap Rough estimate of the entropy change by the liquid/gas volume variation: ∆Svap = R ln (Vg /Vl ) ≈ R ln 1000 ≈ 7R ≈ 57J K−1 mol−1 The remaining contribution of 3R can be attributed to liquid structure. J. Ángyán (EMQC) IMF 26 / 201 Well depths from Trouton’s rule The latent heat of evaporation can be approximated by the energy required to separate the liquid to its constituents is ε (zp energy neglected). The total energy for N molecules, each having n neighbours is ∆Hvap ≈ 10RTb ≈ 1 NA n ε 2 An estimation of of the well-depth, ε is given in terms of Tb ε/kB ≈ 20Tb /n Table: Pair potential well-depths from Trouton’s rule He Ar Xe CH4 H2 O J. Ángyán (EMQC) Tb /K 4.2 87.0 166.0 111.5 373.2 n 12 12 12 12 4 (20Tb /n)/K 7 145 277 186 1866 IMF (ε/kB )/K 11 142 281 180-300 ≈2400 ε/kJ mol−1 0.09 1.18 2.34 1.5-2.50 ≈20 27 / 201 Ionic crystals NaCl crystallizes in fcc lattice lattice parameter a = 5.64Å ions are in (0,0,0) and ( 12 , 12 , 12 ) lattice energy Ulatt = −764.4 kJ/mol Cohesion energy is the sum of the Coulomb (Madelung) and repulsion energy: Ucoh = UC + UR where UC is a lattice sum of 1/r interactions, UR is approximated by the Born-Mayer potential. J. Ángyán (EMQC) IMF 28 / 201 Ionic crystals – Born-Mayer potential Born-Mayer potential: UC = Q2 X (±)j rj−1 UR = j X Be−ri /ρ i The lattice sum (Madelung energy) is conditionally convergent, so special techniques (e.g. Ewald summation) are needed to evaluate them. For a NaCl lattice, the energy can be expressed using the Madelung constant, α = 1.7476, UC = −Q2 2 · 1.7476 2α = −1389.9 × kJ/mol = −861.3kJ/mol a 5.64 The repulsion energy is short-range, therefore it is sufficient to sum over the 6 first-neighbours: X −r /ρ UR = Be i = 6Be−a/2ρ i J. Ángyán (EMQC) IMF 29 / 201 Ionic crystals – parameters of the BM potential The Born-Mayer potential has two unknown parameters, B and ρ. Repulsion energy exp UR = Ucoh − UC = −764.4 + 861.3 = 96.9kJ/mol Condition of equilibrium in the minimum of the lattice energy ∂Ucoh 6B −a/2ρ 2α Uc UR = −Q2 2 − e =− − =0 ∂a a 2ρ a 2ρ Effective "ion radius" is obtained from the repulsion and Madelung energies ρ=− 1 UR · a = 0.3164 2 UC The B parameter of the Born-Mayer potential is B= J. Ángyán (EMQC) UR = 1.168 · 105 kJ/mol 6e−a/2ρ IMF 30 / 201 Ionic crystals – check the potential Second derivative of the cohesion energy „ 2 « ∂ 2 Ucoh ∂ 1 ∂UR Q 2α = − − ∂a2 ∂a a2 2ρ ∂a 1 2 = 2 UC + 2 UR a 4ρ The quality of this potential can be checked by calculating the bulk modulus K=V ∂ 2 Ucoh ∂V 2 where the volume of 1 mole NaCl is V = NA a3 /4. The volume derivative can be calculated as lattice-parameter derivative: „ «−1 ∂V ∂ ∂ = ∂V ∂a ∂a Theoretical bulk modulus „ « 4 2UC UR K= + 9NA a a2 4ρ2 Bulk modulus for the NaCl structure „ «2 2 NA a3 4 ∂ Ucoh K= 4 3NA a2 ∂a2 Conversion to gigapascal 1 kJ/mol/Å3 = 1.667 GPa, i.e. = 14.8016 kJ/mol/Å3 K theor = 24.57 GPa 2 = 4 ∂ Ucoh 9NA a ∂a2 J. Ángyán (EMQC) K exp = 24 GPa IMF 31 / 201 Rare gas crystal Ar crystallizes in fcc lattice lattice parameter a = 5.3109Å ions are in (0,0,0) and ( 12 , 12 , 12 ) lattice energy Ulatt = −8.4732 kJ/mol (after zpe correction) Cohesion energy is the sum of pair potentials Ucoh = N X ULJ (rij ) 2 ij where N = 4, number of atoms in the unit cell, and ULJ is the Lennard-Jones potential: – »“ ” σ 12 “ σ ”6 ULJ (r) = 4ε − r r J. Ángyán (EMQC) IMF 32 / 201 Rare gas crystals - lattice sums Lattice sums can be calculated from √ the number of neighbours at the multiples of the nearest-neighbour distance d = a/ 2: shell r mi 1 d 12 √2 2d 6 √3 3d 24 4 2d 12 √5 5d 24 i fi · d mi General form of the lattice sums „ «n shells shells “ σ ”n “ σ ”n X X σ mi = pn = mi fi−n fi d d d i i Lattice sum for the 6- and 12-potentials Pi p12 = Pi mi fi−12 p6 = i mi fi−6 1 12 12 5 12.13114 14.01839 fcc(∞) 12.13188 14.45392 hcp (∞) 12.13229 14.45489 Cohesion energy of the rare-gas lattice in terms of lattice sums » “ ” “ σ ”6 – Nε σ 12 Ucoh = p12 − p6 2 d d J. Ángyán (EMQC) IMF 33 / 201 Rare gas crystals - fit parameters Stability condition “ σ ”12 1 “ σ ”6 1 ∂Ucoh = −12p12 + 6p6 =0 ∂d d d d d yields the σ parameter as a function of d, the nearest-neighbour distance r 2p12 d= 6 · σ = 1.09026σ p6 Lattice constant a = 1.54186σ. Cohesion energy can be expressed in the function of ε. " „ „ «2 «# p6 p6 Nε − p6 p12 Ucoh = 2 2p12 2p12 or: Ucoh = − J. Ángyán (EMQC) N p26 ε = −2.1525 N ε 8 p12 IMF 34 / 201 Rare gas crystals - structure a = 1.54186 σ Ucoh = −2.1525 N ε Lattice parameters (in Å) and cohesion energies (in µH) from "monomer" Lennard-Jones potentials: Ne Ar Kr Xe re De σ acalc Ucalc aexp Uexp 3.091 3.757 4.008 4.363 133.8 453.5 637.1 893.9 2.75 3.35 3.57 3.89 4.25 5.16 5.51 5.99 1152 3904 5485 7696 4.35 5.23 5.61 6.10 1002 3268 4502 6239 The cohesion energy error is increasing: large cooperative effects. J. Ángyán (EMQC) IMF 35 / 201 Deviations from the ideal gas Equation of state for an ideal gas (noninteracting point masses) P V = RT where P is the pressure, V is molar volume, and R = 8.31J K −1 mol−1 is the gas constant. The standard molar volume V s (1 atm, T=273.15 Ko ) of real gases are different from the ideal value (22414 cm3 ). He: 22377 cm3 CH4 : 22396 cm3 NH3 : 22094 cm3 Considerable deviations can be observed in the behaviour of the compression factor, V . z = PRT J. Ángyán (EMQC) IMF 36 / 201 van der Waals equation of state The van der Waals equation of state accounts for these deviations by introducing two empirical constants, a and b „ « a P + 2 (V − b) = RT V excluded volume in a binary collision 34 πσ 3 b= 2 πNA σ 3 3 reduction of pressure due to intermolecular attraction: the number of binary 2 interactions is proportional to the square of the density, (a/V ) J. Ángyán (EMQC) IMF 37 / 201 van der Waals equation of state Rearrange as V a PV = − RT V −b RT V expanded in the reciprocal volume b − a/RT b2 b3 PV =1+ + 2 + 3 RT V V V repulsive interactions raise the pressure attractive forces reduce the pressure at low T attraction (a), at high T or high pressure repulsion (b) dominates the constants a and b can be obtained from critical parameters Pc , Vc and Tc , where (∂P/∂V )T and ∂ 2 P/∂V 2 )T are both zero: a= J. Ángyán (EMQC) 9 RTc Vc = 3Pc Vc2 8 IMF b= 1 Vc 3 38 / 201 Virial equation of state Virial equation of state – power series of (1/V ) z= B4 PV B2 B3 =1+ + 2 + 3 + ... RT V V V where the second virial coefficient depends on the pair interactions Z B2 (T ) = −2πN ∞` ´ e−u(R)/kT − 1 R2 dR 0 The pair potential u(R) can be obtained by "inversion": mapping measured B2 (T ) points to u(R) – without a priori assumptions. J. Ángyán (EMQC) IMF 39 / 201 Equations of state - generalities The total energy is a function of xα external parameters E = E(x1 , x2 , . . . xn ) Define generalized forces corresponding to external parameters Xα = − ∂E ∂xα In statistical mechanics the equations of state describe the relationship of the external parameters, the generalized forces and the temperature: X α = kT ∂ ln Z ∂xα where Z is the partition function. For the special case of volume (xα = V ) and pressure (X α = P ) ∂ ln Z P = kT ∂V J. Ángyán (EMQC) IMF 40 / 201 The semi-classical partition function ZZ Z 1 . . . e−(K+U )/kT d3 p ~1 d3 p ~2 . . . d3 p ~N d3~r1 d3~r2 . . . d3~rN Z= N !h3N is a product of two terms, depending on the kinetic and the potential energy, respectively: 1X 1 X 2 pj U= ujk K= 2m 2 jk 1 Z= N !h3N ZZ | Z ZZ Z . . . e−K/kT d3 p ~1 d3 p ~2 . . .d3 p ~N . . . e−U/kT d3~r1 d3~r2 . . .d3~rN {z }| {z } ZU (2πmkT )3N/2 Partition function 1 Z= N! J. Ángyán (EMQC) 2πmkT h2 IMF 3N/2 · ZU 41 / 201 Equations of state - ideal gas For an ideal gas uij → 0 (or if T is high kT → ∞) e−U/kT → 1 ZU = V N and the corresponding partition function «– » „ 3 3 1 2πm + N ln V + ln kT + ln ln Zid = ln N! 2 2 h2 Equation of state for an ideal gas P = kT ∂ ln Zid N kT = ∂V V or P V = N kT J. Ángyán (EMQC) IMF 42 / 201 Equations of state - real gas For a real gas with low number density (n = N/V small) an approximate expression can be obtained for the configurational partition function. Take the average potential energy with β = 1/kT , which satisfies the following relationship RRR U e−βU d3~r1 d3~r2 . . . d3~rN ∂ U = RRR −βU 3 3 =− ln ZU ∂β e d ~r1 d ~r2 . . . d3~rN The logarithm of the partition function is β Z ln ZU (β) = N ln V − U (β 0 )dβ 0 0 In a low-density system the U , the average potential energy of 1/2N (N − 1) molecule pairs is equal N 2 /2-fold of the average potential energy of an arbitrary pair of molecules: U= J. Ángyán (EMQC) 1 1 N (N − 1) u ≈ N 2 u 2 2 IMF 43 / 201 The average potential energy of a pair of molecules R Z ~ u(R)e−βu(R) d3 R ∂ ~ u = R −βu(R) =− ln e−βu(R) d3 R ~ ∂β e d3 R Since u(R) = 0 almost everywhere, excepted the small distances, it is worthwhile to transform the integral as Z Z h “ ”i ~ = V + I(β) ~ = 1 + e−βu(R) − 1 d3 R e−βu(R) d3 R The quantity in parentheses is the Mayer-function f (R) = e−βu(R) − 1, and its integral over the intermolecular separation, R is Z ∞“ ” e−βu(R) − 1 R2 dR I(β) = 4π 0 J. Ángyán (EMQC) IMF 44 / 201 Calculate the average potential energy for a pair of molecules » „ «– I(β) ∂ ∂ 1 ∂I(β) u= ln [V + I(β)] = ln V + ln 1 + ≈− · ∂β ∂β V V ∂β which is substituted in the expression of the configurational partition function 1 N2 [I(0) − I(β)] 2 V ln ZU (β) = N ln V + The equation of state is P ∂ ln Z ∂ ln Z N 1 N2 = = = − I(β) kT ∂V ∂VU V 2 V2 or PV PV 4π N = =1− RT N kT 2 V J. Ángyán (EMQC) Z IMF ∞ “ ” e−βu(R) − 1 R2 dR 0 45 / 201 This is the first term of the virial equation of state: z= ∞ X PV Bn+1 =1+ RT Vn n=1 and the virial coefficient is ∞ Z B2 (T ) = −2πN “ ” e−u(R)/kT − 1 R2 dR 0 J. 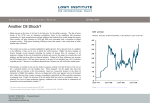Ángyán (EMQC) IMF 46 / 201 Temperature dependence of the virial coefficient J. Ángyán (EMQC) IMF 47 / 201 Temperature dependence of the virial coefficient T \R low small (u > 0) large (u < 0) + –– B2 < 0 + – B2 > 0 kT < u0 high kT > u0 f (R) = e−u(R)/kT − 1 J. Ángyán (EMQC) IMF 48 / 201 Third virial coefficients B3 (T ) = B3add + ∆B3 For a strictly additive potential B3add = − N 3 8π 3 ZZZ f12 f13 f23 r12 r13 r23 dr12 dr13 dr23 The non-additivity correction depends on the 3-body potential ∆U3 ZZZ “ ” N 3 8π e−∆U3 /kT − 1 e−U2 /kT r12 r13 r23 dr12 dr13 dr23 3 For rare gases ∆B3 is up to 50% of the third virial coefficient! ∆B3 = J. Ángyán (EMQC) IMF 49 / 201 VRT spectroscopy Calculated splitting due to tunneling is very sensitive to the height and shape of the barrier – stringent test of the PES. J. Ángyán (EMQC) IMF 50 / 201 Experimental vs. calculated VRT splittings with different water-water potentials. None of the 14 potentials was found to be fully satisfactory. Fellers, Braly, Saykally, Leforestier, J. Chem. Phys. 110 (1999) 6306 J. Ángyán (EMQC) IMF 51 / 201 Further experimental techniques transport properties of gases: thermal conductivity, diffusion coefficient, viscosity lattice vibrations (phonon dispersion) liquid structure: atom-atom pair distribution functions from X-ray and N scattering, diffusion coefficient (velocity autocorrelation function) rotational fine structure of vibrational spectra molecular beam experiments: scattering cross sections etc.... Further reading: Rigby, Smith, Wakeham, Maitland: The forces between molecules, Clarendon Press, Oxford (1986). J. Ángyán (EMQC) IMF 52 / 201 Match theory vs. experiment: advantage theory... J. Ángyán (EMQC) IMF 53 / 201 Part III Long range electrostatic interaction J. Ángyán (EMQC) IMF 54 / 201 Poisson’s equation ∇· Force between two point charges F = therefore q q0 (r − r 0 ) |r − r 0 |3 Z ∇ · E(r) = 4π and the electric field is the force acting on a unit charge in interaction with q 0 placed at the origin: dr 0 δ(r − r 0 )ρ(r 0 ) = 4π ρ(r) Since the field is the negative gradient of the potential: q0 E(r) = r |r|3 E(r) = −∇ · V (r) Using the superposition law, the electric field of a continuous charge distribution Z ρ(r) E(r) = dr 0 (r − r 0 ) |r − r 0 |3 one gets Poisson’s equation ∇2 V (r) = −4π ρ(r) The electrostatic potential is Z ρ(r) V (r) = dr 0 |r − r 0 | Take the divergence of both sides and use J. Ángyán (EMQC) (r − r 0 ) = 4π δ(r − r 0 ) |r − r 0 |3 IMF 55 / 201 Taylor expansion of the electrostatic potential Potential V (R) of the charge distribution %(r) Z %(r) V (R) = dr |R − r| Z = dr T (R − r) %(r) can be expanded in Taylor series around r = 0 (|r| < |R|). Taylor expansion in Cartesian coordinates of the Coulomb interaction function „ « „ « 1 1 X 1 1 XX 1 T (R − r) = − rα ∇α + rα rβ ∇α ∇β R 1! α R 2! α R β „ « X X X 1 1 rα rβ rγ ∇α ∇β ∇γ − + ... 3! α R γ β Attention to alternating signs! J. Ángyán (EMQC) IMF 56 / 201 Expanded electrostatic potential Taylor expansion in the electrostatic potential expression Z Z Z 1 XX V (R) = T (R) dr%(r) − Tα (R) drrα %(r) + Tαβ (R) drrα rβ %(r) 2! α β Z X X X 1 − Tαβγ (R) drrα rβ rγ %(r) + . . . 3! α γ β Cartesian interaction tensors Multipole moments Z q= T (R) = dr%(r) „ « 1 R „ « 1 Tαβ (R) = ∇α ∇β R „ « 1 Tαβγ (R) = ∇α ∇β ∇γ R „ « 1 Tαβ...ν (R) = ∇α ∇β . . . ∇ν R Z mα = Tα (R) = ∇α drrα %(r) Z Qαβ = drrα rβ %(r) Z Oαβγ = drrα rβ rγ %(r) Z ξαβ...ν = J. Ángyán (EMQC) 1 R (n) drrαβ...ν %(r) IMF 57 / 201 Tensor notation generalization of the notion of scalar, vector and matrix its rank is the number of indices rank rank rank rank 0: 1: 2: 3: scalar e.g. charge q vector e.g. dipole µα = {µx , µy , µz } matrix e.g. quadrupole Θαβ e.g octupole Ωαβγ its dimension is the range of the indices (e.g. 3-dimensional) Kronecker delta is defined as  δαβ = 1, 0, if α = β; if α = 6 β. Einstein summation convention over repeated indices: Aαα = Axx + Ayy + Azz = TrA µα V α = µx V x + µy V y + µz V z δαα = δxx + δyy + δzz = 3 J. Ángyán (EMQC) IMF trace contraction (not equal to 1!) 58 / 201 Electrostatic potential, field, field gradient... Using the tensor notation the potential is simply V (R) = qT (R) − mα Tα (R) + (−)n 1 Qαβ Tαβ (R) − . . . + ξαβ...ν Tαβ...ν (R) 2! n! The electric field is the negative gradient of the potential: Fα (R) = −∇α V (R) Since ∇α Tβγ...ν (R) = Tαβγ...ν (R) – the rank of interaction tensor is increased, Fγ (R) = −qTγ (R) + mα Tαγ (R) − 1 Qαβ Tαβγ (R) + . . . 2! It is "easy" to obtain higher derivatives: just add another suffix to the interaction tensors. Field gradient: Fγ (R) = −qTγ (R) + mα Tαγ (R) − J. Ángyán (EMQC) IMF 1 Qαβ Tαβγ (R) + . . . 2! 59 / 201 Let us look at in more details the expansion of the electrostatic potential V (R) = X i qi |R − r i | Expand in Taylor series as V (R) = X qi i  × 1 + riα R „ ∂ 1 ∂riα |R − r i | « + r iα =0 1 riα riβ 2 „ ∂2 1 ∂riα ∂riβ |R − r i | « ff + ... r iα =0 Change derivative w.r.t. riα to Rα (change of sign!): V (R) = X qi i  × „ 1 + riα R − 1 ∂ ∂Rα |R − r i | « + r iα =0 1 riα riβ 2 „ ∂2 1 ∂Rα ∂Rβ |R − r i | ff « + ... r iα =0 Set r iα = 0 V (R) = X i  qi 1 1 1 1 1 1 − riα ∇α + riα riβ ∇α ∇β − riα riβ riγ ∇α ∇β ∇γ + . . . R R 2 R 3! R = qT − mα Tα + J. Ángyán (EMQC) ff 1 1 Qαβ Tαβ − Oαβγ Tαβγ 2 3! IMF 60 / 201 Calculation of cartesian interaction tensors They are defined as T = 1 1 = R−1 = p R Rx2 + Ry2 + Rz2 Use the following derivation rules: ∇α Rβ = δαβ ∇α Rn = nRα R(n−2) ∇α R−n = −nRα R−(n+2) First order Tα (R) = ∇α T (R) = −Rα R−3 Second order Tαβ (R) = ∇α ∇β T (R) = −∇α Rβ R−3 = −δαβ R−3 + 3Rα Rβ R−5 = (3Rα Rβ − R2 δαβ )R−5 Third order Tαβγ (R) = ∇α ∇β ∇γ T (R) = δα (3Rβ Rγ − R2 δβγ )R−5 = 3δαβ Rγ R−5 + 3δαγ Rβ R−5 + 3δβγ Rα R−5 + 3 · 5 · Rα Rβ Rγ R−7 “ ” = 3 5Rα Rβ Rγ − R2 (Rα δβγ + Rβ δγα + Rγ δαβ ) R−7 J. Ángyán (EMQC) IMF 61 / 201 Properties of cartesian interaction tensors Symmetric w.r.t. permutation of indices – order of differentiation does not matter Tαβγ = Tβαγ = Tβγα = . . . Contraction of any pairs of indices gives zero: Tαβ...β...ν = 0 For instance, at second order: Tαα = (3Rα Rα − R2 δαα )R−5 = (3R2 − R2 3)R−5 = 0 (1/R) satisfies the Laplace equation: ∇2 J. Ángyán (EMQC) 1 1 = ∇α ∇α =0 R R IMF 62 / 201 Traced Cartesian multipole moments There are several conventions in the literature to define multipole moments. The previously defined traced cartesian multipole moments Z (n) (n) ξαβ...ν = drrαβ...ν %(r) are symmetric tensors ξαβ = ξβα and their trace is nonzero . X ξαα = ξαα 6= 0 α They are called unnormalized traced Cartesian multipoles. The unabridged multipoles of Applequist differ from them by a normalization factor: (n) µαβ...ν = J. Ángyán (EMQC) 1 (n) ξ n! αβ...ν IMF 63 / 201 Meaning of the trace Spatial extent The trace of the second moment of a charge distribution is used to P characterize its spatial extent, h i ri2 i (a kind of scalar moment of inertia for the electrons). The full charge density can be reconstructed from traced multipoles. Consider the Fourier transform of %(r) Z %(k) = dreikr %(r) and expand the exponential Z Z Z 1 %(k) = dr%(r) +ikα dr rα %(r) − kα kβ dr rα rβ %(r) + . . . 2! {z } | {z } | | {z } q J. Ángyán (EMQC) mα IMF Qαβ 64 / 201 Traceless Cartesian multipoles (Buckingham) Potential of the second moment V (2) (R) = Since the T (R) = 1 R 1 Qαβ Tαβ (R) 2 function satisfies the Laplace equation „ « 1 ∇2 =0 R « „ X X 1 ∇α ∇α = Tαα (R) = 0 R α α we can add to the quadrupole potential an arbitrary quantity λδαβ Tαβ (R) without changing its value V (2) (R) = J. Ángyán (EMQC) 1 (Qαβ + λδαβ ) Tαβ (R) 2 IMF 65 / 201 Let us choose λ such as the trace of Qαβ 1 1X λ = − Qαα = − Qαα = r2 3 3 α The new expression of the quadrupole potential Z ” “ 1 1 V (2) (R) = · dr 3rα rβ − r2 δαβ %(r)Tαβ (R) 2 3 1 = Θαβ Tαβ (R) 3 in terms of the traceless cartesian quadrupole moment Z ” “ 1 Θαβ = dr 3rα rβ − r2 δαβ %(r) 2 J. Ángyán (EMQC) IMF 66 / 201 Traceless (Buckingham) multipole moments General definition (n) Mαβ...ν = (−)n n! Z dr%(r)r2n+1 ∂n ∂rα ∂ . . . rν „ « 1 r Electrostatic potential V (R) = X n (−)n (n) (n) M T (R) (2n − 1)!! αβ...ν αβ...ν where the notation (2n − 1)!! means (2n − 1)!! = 1 · 3 · 5 · . . . (2n − 1) The traceless multipoles do not contain the full information about the %(r) charge distribution, since they are undetermined up to an arbitrary spherically symmetric component. Example of quadrupole: Z 1 (2) dr%(r) r5 (3rα rβ − δαβ r2 )r−5 = Θαβ Mαβ = 2 J. Ángyán (EMQC) IMF 67 / 201 Dipole moments Typical values of dipole moments H2O H2S HF HCl HBr HI CO NH3 PH3 AsH3 NaCl H2CO CH3CN D 1.85 0.98 1.91 1.08 0.80 0.42 0.12 1.47 0.58 0.20 9.00 2.33 3.91 J. Ángyán (EMQC) a.u. 0.728 0.386 0.751 0.425 0.315 0.165 0.047 0.578 0.228 0.079 3.541 0.917 1.538 1030 Cm 6.17 3.27 6.37 3.60 2.67 1.40 0.40 4.90 1.93 0.67 30.02 7.77 13.04 Traditional unit is Debye: 1 D=10−18 e.s.u. SI units are impractical 1 D = 3.33564×10−30 C m 1 C m = 0.29979×1030 D 1 C m = 0.11795×10−30 a.u. Atomic units are convenient: 1 a.u. = 2.54177 D 1 a.u. = 8.47836×10−30 C m IMF 68 / 201 Quantum chemical calculation of dipole moments Good basis set with polarization function needed Hartree-Fock overestimates dipole moments Correlated methods are recommended DFT methods are usually not too bad Mol CO H2 O H2 S HF HCl NH3 PH3 SO2 HF/POL -0.25 1.98 1.11 1.92 1.21 1.62 0.71 1.99 J. Ángyán (EMQC) MP2/POL 0.31 1.85 1.03 1.80 1.14 1.52 0.62 1.54 BLYP/POL 0.19 1.80 0.97 1.75 1.08 1.48 0.59 1.57 IMF B3LYP/cc-pVTZ 0.13 1.92 1.19 1.83 1.21 1.59 0.53 2.01 B3LYP/POL 0.10 1.86 1.01 1.80 1.12 1.52 0.62 1.67 exp. 0.12 1.85 0.98 1.83 1.11 1.47 0.58 1.63 69 / 201 Quadrupole moments Quadrupole moment is a second-order tensor: matrix 0 3xi xi − ri2 3xi yi 1 X @ 3xi yi 3yi yi − ri2 Θ= qi 2 i 3xi zi 3yi zi 1 3xi zi A 3yi zi 2 3zi zi − ri tensor notations: Θαβ = ´ 1 X ` qi 3riα riβ − ri2 δαβ 2 i Symmetrical Traceless Has the dimensions of [charge]×[length]2 , so the atomic units are ea20 = 4.49 × 10−40 C m Other units: Buckinghams (B) 1 B = 1 DÅ= 10−26 e.s.u. 1 a.u. =1.3450×10−26 e.s.u. = 4.487×10−40 C m2 J. Ángyán (EMQC) IMF 70 / 201 Estimation of quadrupole moments The traceless quadrupole moment tensor has five independent components: Θαβ = Θβα Trace is zero: Θαα = 0 Independent components: Θzz , Θxx − Θyy , Θxy , Θyz , Θxz For systems with axial symmetry, Θxx − Θyy = 0 and we have Θzz = 1 X qi (3zi2 − ri2 ) 2 i 1 X z2 qi ri2 (3 i2 − 1) 2 i ri 1 X = qi ri2 (3 cos θ2 − 1) 2 i = Angular function 1/2(3 cos θ2 − 1) > 0 near the z-axis (θ < 54.736◦ or θ > 125.264◦ ) so positive charge in these regions contribute positively, while positive charge near the xy plane (54.736◦ < θ < 125.264◦ ) contribute negatively. J. Ángyán (EMQC) IMF 71 / 201 Quadrupole moments BX3 CO2 Negatively charged O atoms on the z axis lead to negative quadrupole moment of -3.3 a.u. J. Ángyán (EMQC) Negatively charged X(=F,Cl) atoms in the xy plane lead to a positive quadrupole moment: BF3 ∼ 2.5 a.u.; BCl3 ∼ 1.5 a.u. (Theory: 3.0 a.u. and 0.8 a.u.) IMF 72 / 201 Some experimental quadrupole moments Water (xz plane −z axis to O ) Molecule H2 N2 HCl CO benzene C6 F6 ethane C3 H3 NH3 DÅ +0.6 -1.4 +3.8 -2.5 -8.5 +9.5 -0.8 +1.6 -2.3 J. Ángyán (EMQC) a.u. +0.45 -1.04 +2.83 -1.86 -6.32 +7.06 -0.59 +1.19 -1.71 10−40 Cm2 +2.1 -4.9 +12.3 -8.2 -29.7 +31.7 -2.7 +5.3 -7.7 0 +2.63 0 Θ=@ 0 0 −2.50 0 1 0 A 0 −0.13 H2 C=CH2 (yz plane z axis along C=C) 0 −3.25 0 Θ=@ 0 IMF 0 +1.62 0 1 0 A 0 +1.62 73 / 201 Change of origin: dipole moments Dipole moment of a point charge distribution X µα = qi riα i In a new frame obtained after a translation by a vector R X X X µ0α = qi (riα − Rα ) = qi riα − Rα qi = µα − Rα qtot i i i Dipole of a neutral system (qtot = 0) is invariant to translation of origin. Dipole moment of a charged system can always be set zero if the origin is at the center of charge (barycenter). J. Ángyán (EMQC) IMF 74 / 201 Change of origin: quadrupole moment Change of origin; r 0 = r − R ´ 1` 3(r − R)α (r − R)β − |r − R|2 δαβ 2 3 3 1 = Θαβ − Rα µβ − Rβ µα + µ · Rδαβ + q(3Rα Rβ − R2 δαβ ) 2 2 2 Θ0αβ = In general, it is not possible to find a center of dipole (5 quadrupole components to be annihilated, only 3 translational degrees of freedom) For molecules with 3-fold (or higher) axis of symmetry Θzz = −2Θxx = −2Θyy and only 1 nonzero dipole (µz ): Θ0zz = Θzz − 2Rz µz thus Rz = 12 Θzz µ−1 z is the center of dipole J. Ángyán (EMQC) IMF 75 / 201 Change of origin: quadrupole moment Quadrupole relative to the center of mass Quadrupole relative to the H atom Θzz > 0 Θzz < 0 Hydrogen fluoride molecule J. Ángyán (EMQC) IMF 76 / 201 Electrostatic energy Work to assemble a set of point charges qi at r i is U= The charge distribution is partitioned to two (or more) pieces: 1X qi V (r i ) 2 i B %r = %A r + %r Total electrostatic energy splits on several contributions: Generalized for continuous charge distributions Z 1 U= dr%(r) V (r) 2 U= splits to a self-energy contribution Using the expression of the potential we obtain the total electrostatic energy ZZ %(r)%(r 0 ) 1 drdr 0 U= 2 |r − r 0 | J. Ángyán (EMQC) 1 1 B B A Uself = %A %r %r0 Trr0 r %r 0 Trr 0 + 2 2 and an interaction energy B Uint = %A r %r 0 Trr 0 Shorthand notation U= 1 A A B (%r + %B r )(%r 0 + %r 0 ) Trr 0 2 We are interested in the electrostatic interaction energy 1 %r %r0 Trr0 2 IMF 77 / 201 Electrostatic interaction energy Electrostatic interaction energy of two charge distributions is the interaction of one charge distribution with the potential of the other. ZZ U= %A (r)%B (r 0 ) |r − r 0 | Z dr%A (r)V B (r) Z dr 0 %B (r 0 )V A (r 0 ) = = drdr 0 We know how to calculate the potential created by a charge distribution; what is the energy of %(r) in an external potential? J. Ángyán (EMQC) IMF 78 / 201 Charge distribution in an external potential Choose the origin inside the charge distribution, %(r) and expand the external potential in Taylor series around the origin V (r) = V (0) + rα Vα (0) + 1 1 rα rβ Vαβ (0) + rα rβ rγ Vαβγ (0) + . . . 2! 3! From the expression of the interaction energy Z Z Z U = dr%(r)V (r) = dr%(r)V (0) + dr%(r)rα Vα (0) Z Z 1 1 + dr%(r)rα rβ Vαβ (0) + dr%(r)rα rβ rγ Vαβγ (0) + . . . 2! 3! where one recognizes the unnormalized traced multipoles, U = ξV + ξα Vα + J. Ángyán (EMQC) 1 1 ξαβ Vαβ + ξαβγ Vαβγ + . . . 2! 3! IMF 79 / 201 Interaction with external potential By the virtue of the Laplace equation, Vαα = 0, the trace of ξαβ = Qαβ , i.e. 13 Qαα can be subtracted from the quadrupolar energy 1 1 1 1 Qαβ Vαβ = Vαβ (Qαβ − δαβ Qαα ) = Vαβ Θαβ 2 2 3 3 By similar manipulations at higher orders one obtains the interaction energy in terms of traceless Buckingham multipole moments 1 1 Θαβ Vαβ + Ωαβγ Vαβγ 3 3·5 1 1 (n) + Φαβγδ Vαβγδ + Mα...ν Vα...ν 3·5·7 (2n − 1)!! U = qV + µα Vα + The energy is the scalar product of the field with dipole, field gradient with quadrupole and higher field gradients with the corresponding multipole tensors. Attention: the result may depend on the choice of origin! J. Ángyán (EMQC) IMF 80 / 201 Multipoles in field, field gradient Quadrupole/field-gradient interaction Dipole/field interaction U= U = Fx µx + Fy µy < 0 J. Ángyán (EMQC) IMF 1 Fxy Θxy > 0 3 81 / 201 Multipole-multipole interaction energy Take two sets of multipoles. Double Taylor series of the Coulomb interaction 1 1 1 = = = |τ − τ 0 | |B + s − A − r| |R − (r − s)| „ « „ « 1 1 1 1 = + (rα − sα )∇α + (rα − sα )(rβ − sβ )∇α ∇β + ... R R 2! R which leads directly to an expression of the interaction energy of two multipole charge distributions in terms of their traced Cartesian moments B A U (R) = q A q B T (R) + (mA α q − q mα ) Tα (R) 1 B A B A B A B + (QA αβ q + q Qαβ − mα mβ − mβ mα ) Tαβ (R) + . . . 2! Using the traceless (Buckingham) moments U (R) = X `1 `2 J. Ángyán (EMQC) (−)`1 )[A] (`1 +`2 ) )[B] Mα(`11...ν T (R)Mα(`22...ν 1 α1 ...ν1 α2 ...ν2 2 (2`1 − 1)!!(2`2 − 1)!! IMF 82 / 201 Multipole interactions - general remarks Multipole-multipole interactions with traceless moments: B A U = q A T q B + µA α Tα q − q Tα µα 1 A 1 B − µA Θαβ Tαβ q B + q A Tαβ ΘB α Tαβ µβ + αβ 3 3 1 A 1 1 A 1 A B q Tαβγ ΩB Ωαβγ Tαβγ q B − µA Θβγ Tαβγ µB + αβγ − α Tαβγ Θβγ + α 15 15 3 3 1 A + Θαβ Tαβγδ ΘB γδ + . . . 9 The interaction between multipoles of rank [nA ] and rank [nB ] is: U = M [nA ] M [nB ] × R−nA −nB −1 × angular factor Strongly orientation dependent Electrostatic energy can be truncated either by the highest rank of multipole (e.g. up to Θ-Θ) or by the highest rank of the interaction tensor (e.g. up to R−5 , including q-Φ interactions). J. Ángyán (EMQC) IMF 83 / 201 Summary of multipole-multipole interactions J. Ángyán (EMQC) IMF 84 / 201 Dipole-dipole interaction Dipole-dipole interaction energy B Uµµ = −µA α Tαβ µβ 3Rα Rβ − R2 δαβ B µβ R5 µA · µB − 3 (µA · R̂) (µB · R̂) = R3 = −µA α A convenient setting of the coordinates is the z axis along the intermolecular vector from A to B. The dipoles are specified by their polar angles. 0 1 0 R = @ 0 A, R J. Ángyán (EMQC) 0 µA 1 sin θA cos φA = µA @ sin θA sin φA A cos θA IMF 0 µB 1 sin θB cos φB = µB @ sin θB sin φB A cos θB 85 / 201 Dipole-dipole interaction The dipole-dipole interaction energy becomes Uµµ = − ´ µA µB ` 2 cos θA cos θB − sin θA sin θB cos φ R3 with φ = φB − φA The most favorable orientation at a given distance R is θA = θB = 0, where the interaction energy is −2µA µB /R3 . Another favorable orientation is θA = θB = π/2, φ = π, with the interaction energy −µA µB /R3 J. Ángyán (EMQC) IMF 86 / 201 Dipole-quadrupole interaction Dipole-quadrupole interaction energy of two linear molecules: UµΘ = − ´ 3µA ΘB ` 2 sin θA sin θB cos θB cos φ − cos θA (3 cos2 θB − 1) 2R4 Some of the special configurations: J. Ángyán (EMQC) IMF 87 / 201 Quadrupole-quadrupole interaction Quadrupole-quadrupole interaction energy between two symmetric top molecules. non-zero quadrupole moment components are Θzz = Θ and Θxx = Θyy = − 12 Θ UΘΘ = 3ΘA ΘB ˆ 1 − 5 cos2 θA − 5 cos2 θB − 15 cos2 θA cos2 θB 4R5 ˜ + 2(4 cos θA cos θB − sin θA sin θB cos φ)2 The most favorable structures are the T-shaped and slipped parallel. Both of these occur sometimes in the same crystal structures of quadrupolar molecules (e.g. N2 , CO, benzene). J. Ángyán (EMQC) IMF 88 / 201 Interaction of two HX molecules Competition of three multipolar interactions. Angular dependence for linear molecules (symmetric tops) is the following: dipole-dipole Uµµ = − µA µB (2 cos θA cos θB − sin θA sin θB cos ϕ) R3 dipole-quadrupole UµΘ = 3µA ΘB [cos θA (3 cos2 θB − 1) − sin θA sin 2θB cos ϕ] 4R4 quadrupole-quadrupole ΘA ΘB 3 [1 − 5 cos2 θA − 5 cos2 θB − 15 cos2 θA cos2 θB R5 4 + 2(4 cos θA cos θB − sin θA sin θB cos ϕ)2 ] UΘΘ = J. Ángyán (EMQC) IMF 89 / 201 The structure is characterized by θA ≈ 0 and ϕ = 0, µA = µB = µ and ΘA = ΘB = Θ. The sum of the 4 interaction terms (two for UµΘ ) µ2 · 2 cos θ R3 µΘ 3 + 4 · [(3 cos2 θ − 1) − 2 cos θ] R 2 Θ2 + 5 · 3(3 cos2 θ − 1) R U =− Introduce the parameter λ = Θ µR ¯ 3 µ2 ˘ −2 cos θ + λ [(3 cos2 θ − 1) − 2 cos θ] + λ2 3(3 cos2 θ − 1) 3 R 2 ¯ µ2 ˘ = 3λ(1 + 2λ)(3 cos2 θ − 1) − 2(2 + 3λ) cos θ 3 2R U= J. Ángyán (EMQC) IMF 90 / 201 Electrostatic interaction energy is plotted for the HF dimer µ = 0.72ea0 , Θ = 1.875ea20 R = 5.1a0 ; minimum at 68 degrees (exp. 60) HCl dimer µ = 0.433ea0 , Θ = 2.8ea20 R = 6.8a0 ; minimum at 79 degrees J. Ángyán (EMQC) IMF 91 / 201 Legendre expansion of the potential The distance |R − r| can be expressed with the help of the cosine rule (R − r) · (R − r) = R2 + r2 − 2Rr cos γ The Coulomb interaction T (R−r) = 1/|R−r| can be written in two alternative forms 8 h i−1/2 ` r ´2 `r´ > > R1 1 + R if r < R, − 2 cos γ > R < T (R − r) = > h i−1/2 > > : 1 1 + ` R ´2 − 2` R ´ cos γ r r r J. Ángyán (EMQC) IMF if r > R. 92 / 201 The expression in brackets is just the generator function of the Legendre polynomials (1 + t2 − 2t cos γ)−1/2 = ∞ X Pl (cos γ) tl |t| < 1 l The first few Legendre polynomials P0 (x) = 1 P1 (x) = x 1 P2 (x) = (3x2 − 1) 2 1 P3 (x) = (5x3 − 3x) 2 1 P4 (x) = (35x4 − 30x2 + 3) 8 and at an arbitrary order they can be obtained from the recurrence relation (2l + 1)xPl = (l + 1)Pl+1 + lPl−1 J. Ángyán (EMQC) IMF 93 / 201 Depending on the space domains, either the first (r < R), or the second (R < r) form of the generator function can be applied: 8P∞ l r > < l Rl+1 Pl (cos γ) if r < R T (R − r) = > :P∞ Rl if r > R l r l+1 Pl (cos γ) The formulae for the two domains of space (r < R, r > R) are usually expressed in the following condensed form T (R − r) = ∞ l X r< Pl (cos γ) rl+1 l=0 > The lowest-order terms explicitly for r = |r| |R| 3(r · R)2 − r2 R2 5(r · R)3 − 3 (r · R) r2 R2 1 1 r·R = + + + + ... 3 5 |R − r| R R 2R 2R7 where we used that r R cos γ = r · R J. Ángyán (EMQC) IMF 94 / 201 Exercises Find the 4th order term of the Legendre expansion of 1/|R − r| in the above form (i.e. using scalar products of the vectors r and R). Derive the Legendre expansion in the above form up to 4th order making use of the series expansion 1 x 3x2 5x3 35x4 √ =1− + − + − ... 2 8 16 128 1+x J. Ángyán (EMQC) IMF 95 / 201 Spherical harmonic expansion Addition theorem of spherical harmonics „ Pl (cos γ) = 4π 2l + 1 « X l ∗ Ylm (ω)Ylm (Ω) m=−l where ω = (θ, φ) and Ω = (Θ, Φ) are the angular components of the polar coordinates of r and R, respectively. The (complex) spherical harmonics for m ≥ 0 Ylm (ω) = (−)m „ 2l + 1 4π «„ (l − m)! (l + m)! «1/2 P`m (cos θ) exp(imφ) and for m ≤ 0 ∗ Ylm (ω) = (−)m Ylm (ω) J. Ángyán (EMQC) IMF 96 / 201 Here we used the associated Legendre polynomials, that are defined for m > 0 through the derivatives of Pl (x) as „ «m d P`m (x) = (1 − x2 )m/2 P` (x) dx P00 (cos θ) = 1 P10 (cos θ) = cos θ P11 (cos θ) = sin θ 1 P20 (cos θ) = (3 cos2 θ − 1) 2 P21 (cos θ) = 3 sin θ cos θ P22 (cos θ) = 3 sin2 θ Finally, we obtain the spherical harmonics form of the interaction kernel „ T (R − r) = J. Ángyán (EMQC) 4π 2l + 1 «X ∞ X l l r< ∗ Ylm (ω)Ylm (Ω) rl+1 l=0 m=−l > IMF 97 / 201 Potential outside of the charge distribution If the charge distribution %(r) vanishes in the points R where we want to calculate the potential, the condition r < R is always satisfied V (R) = « Z ∞ X ` „ X 4π ∗ Y`m (Ω)R−`−1 drY`m (ω)r` %(r) 2l + 1 `=0 m=−` Define the modified spherical harmonics „ C`m (ω) = 4π 2l + 1 «1/2 Y`m (ω) as well as the regular, R`m (r), and irregular, I`m (r), spherical harmonics I`m (r) = r−`−1 C`m (ω) R`m (r) = r` C`m (ω) J. Ángyán (EMQC) IMF 98 / 201 Using these functions, in terms of complex spherical harmonics multipole moments, Q`m Z Q`m = drR`m (r)%(r) the potential becomes V (R) = ∞ X ` X Z ∞ X ` X (−) I`m (R) drR`m (r)%(r) = (−)m I`m (R)Q`m m `=0 m=−` `=0 m=−` It is more practical to use real spherical harmonics instead the complex ones r 1 Q`mc = [(−)m Q`m + Q`m ] 2 r 1 Q`ms = [(−)m Q`m − Q`m ] 2 The absolute value of the multipole moment 2 Q` = ` X Q`m Q∗`m = X Q2`κ κ m=−` This quantity is invariant with respect to the orientation of the frame. J. Ángyán (EMQC) IMF 99 / 201 Transformation of spherical and cartesian moments Relationship of the real spherical harmonics and Cartesian multipole moments Q`mc/s Q00 Q10 Q11c Q11s Q20 Q21c Q21s Q22c Q22s J. Ángyán (EMQC) (n) ξα...ν q mz mx my 1 (2Qzz − Qxx − Qyy ) 2 √ 3Qxz √ 3Qyz √ 3 (Qxx 2 − Qyy ) √ 3Qxy IMF (n) Mα...ν q µz µx µy Θ q zz 4 q3 Θxz 4 Θ 3 yz √1 (Θxx − Θyy ) 3 q 4 Θ 3 xy 100 / 201 Spherical harmonics expansion of the interaction One can obtain the bipolar expansion by applying the previously derived result for |r B − r A | < |R| 1 |R + r B − r A | = ∞ X l X (−)m Rlm (r B − r A )Ilm (R) l=0 m=−l According to the addition theorem of regular spherical harmonics Rlm (r B + r A ) = X X δlA +lB ,l (−)l−m lA lB mA mB „ × „ where lA lB mA mB J. Ángyán (EMQC) lA lB mA mB „ (2l + 1)! (2lA )!(2lB )! «1/2 × « l RlA mA (r A )RlB mB (r B ) m « l a Wigner 3j coefficient. m IMF 101 / 201 Use that Rlm (−r) = (−)l Rlm (r), and the multipole expansion of the interaction energy becomes „ «1/2 X X (2lA + 2lB + 1)! U (R) = (−)lB × (2lA )!(2lB )! lA lB mA mB m „ « lA lB lA + lB B × QA lA mA QlB mB IlA +lB ,m (R) mA mB m The multipole moments are expressed in a global coordinate system. Transform the multipoles to a local coordinate system X l Q̃lk = Qlm Dmk (Ω) m where Ω = (α, β, γ) is the rotation that takes the global axes to the local ones, and l Dmk (Ω) are the elements of the (hermitian) Wigner rotation matrices.Inversely, the global multipole components can be written in terms of the local ones X X l l Qlm = Q̃lk Dkm (Ω−1 ) = Q̃lk [Dkm (Ω)]∗ k J. Ángyán (EMQC) k IMF 102 / 201 Insert the local-frame multipole moments and define a new orientation-dependent function »„ «–−1 lA lB j × S̄lkAAlkBBj = ilA −lB −j 0 0 0 „ « X lA lB lA + lB lA lB ∗ ∗ × [DkA mA (ΩA )] [DkB mB (ΩB )] Cjm (θ, φ) mA mB m mA mB m where θ, φ are the polar angles of the intermolecular vector. In terms of these functions and expanding the Wigner 3j symbols one obtains X X „lA + lB « A mA mB −lA −lB −1 U (R) = Q̃lA mA Q̃B lB mB S̄lA lB lA +lB R lA lA lB mA mB m or after transformation to real components X X „lA + lB « A κA κB −lA −lB −1 U (R) = Q̃lA κA Q̃B lB κB S̄lA lB lA +lB R lA lA lB κA κB m J. Ángyán (EMQC) IMF 103 / 201 One can define the spherical analogue of the interaction tensors „ « lA + lB S̄lκ11l2κl21 +l2 R−l1 −l2 −1 Tl1 κ1 ,l2 κ2 = lA and the electrostatic interaction energy (operator) takes the simple form X A AB B X X Q̃t Ttu Q̃u U= Q̃A lA κA TlA κA ,lB κB Q̃lB κB = tu lA lB κA κB m with t, u = {lκ}. The T tensors can be expressed in terms of the unit vectors of the respective local coordinate systems, and the vector R. J. Ángyán (EMQC) IMF 104 / 201 Interaction tensors between local frames Following the derivation of Hättig and Heß (Mol.Phys. 81 (1994) 813), the interaction energy in space-fixed frame ZZ %A (r)%B SF (s) U= drds SF |s − r| Let us write the rotation matrices from the space-fixed (global) to the molecule-fixed (local) frame as R̂(ΩA ) and R̂(ΩB ), where Ω = (α, β, γ) are the Euler angles, and the coordinates r = A + R̂(ΩA )r A and s = B + R̂(ΩB )r B Use the notation R = B − A and that the length of a vector does not change by rotation |s − r| = |R + R̂(ΩB )r B − R̂(ΩA )r A | = |R̂−1 (ΩA )R + R̂−1 (ΩA )R̂(ΩB )r B − r A | J. Ángyán (EMQC) IMF 105 / 201 Electrostatic energy in molecule-fixed charge distributions ZZ B %A MF (r A )%MF (r B ) = U= dr A dr B |R̂−1 (ΩA )R + R̂−1 (ΩA )R̂(ΩB )r B − r A | Z ∞ X X = QA dr B Il1 κ1 (R̂−1 (ΩA )R + R̂−1 (ΩA )R̂(ΩB )r B ) · %B l1 κ1 · MF (r B ) l1 κ1 The irregular spherical harmonics can be expanded in Taylor series −1 −1 Il1 κ1 (R̂A R + R̂A R̂B r B ) = = ∞ X 1 −1 R) = (R̂−1 R̂B r B · ∇R̂−1 R )l2 · Il1 κ1 (R̂A A l2 ! A l2 =0 = ∞ X 1 −1 R) (r B · ∇R̂−1 R )l2 · Il1 κ1 (R̂A B l2 ! l2 =0 J. Ángyán (EMQC) IMF 106 / 201 and in terms of spherical tensors as −1 −1 Il1 κ1 (R̂A R + R̂A R̂B r B ) = = ∞ X X l2 =0 κ2 1 −1 R) Rl κ (r B ) · Rl2 κ2 (∇R̂−1 R ) · Il1 κ1 (R̂A B (2l2 − 1)!! 2 2 Using the identity Ilκ (R) = (−)l Rlκ (∇)(1/R), the interaction energy becomes U= ∞ XX ∞ X X l1 κ1 l2 B AB QA l1 κ1 · Ql2 κ2 · Tl1 κ1 l2 κ2 κ2 with TlAB interaction tensor 1 κ1 l2 κ2 TlAB (R, ΩA , ΩB ) = 1 κ1 l2 κ2 J. Ángyán (EMQC) (−)l1 1 1 −1 · Rl κ (R̂−1 ∇R )Rl1 κ1 (R̂A ∇R ) (2l1 − 1)!! (2l2 − 1)!! 2 2 B R IMF 107 / 201 The rotated internuclear vector and the rotated differential operators can be expressed in terms of direction cosines and the internuclear distance R. The rotation matrices can be written in terms of the unit vectors of the molecule fixed frame in the space-fixed system (A) (A) R̂A = (e(A) x , ey , ez ) and (B) (B) R̂B = (e(B) x , ey , ex ) (A) A the intermolecular unit vector, eAB = R/R and the direction cosines, rα = eα · eAB and (B) cαβ = eβ · e(A) α . For instance 1 A2 (3rα − 1)R−3 2 A B = (3rα rβ + cαβ )R−3 T20,00 = T1α,1β Computation of the general expressions in both cartesian and spherical tensors are quite costly and scale as L6 , where L is the order of 1/R expansion. Using an intermediate coordinate transformation, Hättig derived general recurrence relations, which scale as L4 (CPL, 260(1996)341). J. Ángyán (EMQC) IMF 108 / 201 J. Ángyán (EMQC) IMF 109 / 201 Part IV Induction energy J. Ángyán (EMQC) IMF 110 / 201 Electrostatic interaction Hamiltonian Place a molecule in an external electrostatic field. The interaction Hamiltonian is X V̂ = qk V (r k ) with qk = e, Z k Let us define the operator of the total charge density X X %̂(r) = Zα δ(r − Rα ) − δ(r − r i ) α i permitting to express the interaction Hamiltonian in the compact form as Z V̂ = dr %̂(r) V (r) J. Ángyán (EMQC) IMF 111 / 201 Molecule in a uniform electric field Place molecules between two plates of a capacitor: The electrostatic potential can be written in terms of the 3 components of the uniform electric field X V (r) = V0 + Fα rα = V0 + Fα rα α (Einstein summation convention on repeated indices) The interaction operator with the field of the capacitor simplifies as Z V̂ = dr %̂(r) (V0 + Fα rα ) = V0 q̂ + Fα µ̂α where the operators of the total charge and total dipole moment of the molecule are Z Z q̂ = dr %̂(r) µ̂α = dr %̂(r)rα J. Ángyán (EMQC) IMF 112 / 201 Schrödinger equation with perturbation We are looking for the ground state solution of the problem Ĥψ = (Ĥ0 + V̂ )ψ = Eψ and we already know the (exact) solution of the zero-order problem Ĥ0 ϕ0 = E0 ϕ0 Let us write ∆E = E − E0 , the energy correction (Ĥ0 − E0 )ψ = (∆E − V̂ )ψ and in order to fix the phase of ψ, impose the intermediate normalization hϕ0 |ψi = 1 J. Ángyán (EMQC) IMF 113 / 201 Introduce the reduced resolvent operator as R̂0 = (1 − |ϕ0 ihϕ0 |)(Ĥ0 − E0 )−1 which can be regarded as the inverse of the operator Ĥ0 − E0 in the space of functions orthogonal to ϕ0 R̂0 (Ĥ0 − E0 ) = 1 − |ϕ0 ihϕ0 | Multiplying the Schrödinger equation by R̂0 R̂0 (Ĥ0 − E0 )ψ = R̂0 (∆E − V̂ )ψ using the definition of the resolvent and the intermediate normalization an equation is obtained for the wave function ψ = ϕ0 + R̂0 (∆E − V̂ )ψ After multiplication of the Schrödinger equation by hϕ0 | hϕ0 |(Ĥ0 − E0 )|ψi = hϕ0 |(∆E − V̂ )|ψi we get the energy correction ∆E = hϕ0 |V̂ |ψi J. Ángyán (EMQC) IMF 114 / 201 Iterative solution These equations can be solved iteratively ∆En = hϕ0 |V̂ |ψn−1 i ψn = ϕ0 + R̂0 (∆En − V̂ )ψn−1 To the lowest orders of iteration we find by using ψ0 = ϕ0 and R̂0 ϕ0 = 0 ∆E1 = hϕ0 |V̂ |ψ0 i ψ1 = ϕ0 − R̂0 V̂ ψ0 ∆E2 = hϕ0 |V̂ |ψ1 i = hϕ0 |V̂ |ψ0 i − hϕ0 |V̂ R̂0 V̂ |ψ0 i = ∆E1 − hϕ0 |V̂ R̂0 V̂ |ψ0 i ψ2 = ϕ0 − R̂0 (∆E2 − V̂ )ψ1 = ϕ0 − R̂0 (hϕ0 |V̂ |ψ0 i − hϕ0 |V̂ R̂0 V̂ |ψ0 i − V̂ )(ϕ0 − R̂0 V̂ ψ0 ) = ϕ(1) − R̂0 (V̂ − ∆E2 )R̂0 V̂ ϕ0 J. Ángyán (EMQC) IMF 115 / 201 H-atom in electric field Hamiltonian of the H-atom in an electric field, Fz Ĥ = Ĥ0 + ẑFz where 1 1 Ĥ0 = − ∆ − 2 r The Hamiltonian of the isolated H-atom has the lowest eigenvalue E0 = − 12 and eigenfunction ϕ0 = First iteration in the energy yields zero √1 e−r . π ∆E1 = Fz hϕ0 |ẑ|ψ0 i = µz · Fz = 0 First iteration in the wave function leads to the equation ψ1 = ϕ0 − R̂0 V̂ ϕ0 “ ” (Ĥ0 − E0 )ψ1 = − V̂ − ∆E1 ϕ0 „ « 1 1 1 1 − ∆− + ψ1 = − √ Fz z e−r 2 r 2 π which has the solution J. Ángyán (EMQC) “r ” Fz ψ1 = − √ z − 1 e−r 2 π IMF 116 / 201 Second energy iteration 9 · Fz2 4 This leads to a development of the energy in the powers of Fz ∆E2 = Fz hϕ0 |ẑ|ψ1 i = − E = E0 + ∆E2 = E0 − 9 · Fz2 4 the dipole polarizability is „ α=− J. Ángyán (EMQC) ∂2E ∂Fz2 « = Fz =0 IMF 9 a.u. 2 117 / 201 Perturbation approach Assuming that the iteration process converges, the exact wave function and energy can be expanded in power series of a perturbation parameter λ (Ĥ0 + λV̂ )ψ = ∆Eψ as ∆E = ∞ X λn ∆E (n) and ψ= n=1 ∞ X λn ψ (n) n=0 Substitute the series expansions in ∆E = hϕ0 |V̂ |ψi ψ = ϕ0 + R̂0 (∆E − V̂ )ψ and leading to X λn ∆E (n) = n=1 X λm+1 hϕ0 |V̂ |ψ (m) i m=0 ! X n=1 J. Ángyán (EMQC) n λ ψ (n) = ϕ0 + R̂0 X m λ ∆E m=1 IMF (m) − λV̂ X λk ψ (k) k=1 118 / 201 Collect terms of the same power in λ to obtain the general recursion formulae ∆E (n) = hϕ0 |V̂ |ψ (n−1) i ψ (n) = −R̂0 V̂ ψ (n−1) − n−1 X ∆E (k) R̂0 ψ (n−k) k=1 The reduced resolvent has the spectral resolution R̂0 = X |ϕ0 ihϕ0 | E k − E0 k6=0 J. Ángyán (EMQC) IMF 119 / 201 First order ψ (1) ∆E (1) = hϕ0 |V̂ |ϕ0 i X hϕk |V̂ |ϕ0 i ϕk = −R̂0 V̂ ϕ0 = − Ek − E0 k6=0 The wave function corrections are often expressed in terms of the expansion coefficients (n) ck = hϕk |ψ (n) i on the basis of the eigenfunctions of the zero order Hamiltonian X hϕk |V̂ |ϕ0 i (1) ck = − Ek − E0 k6=0 J. Ángyán (EMQC) IMF 120 / 201 Second order Energy E (2) =hϕ0 |V̂ |ψ (1) i = −hϕ0 |V̂ R̂0 V̂ |ϕ0 i X hϕ0 |V̂ |ϕk ihϕk |V̂ |ϕ0 i =− Ek − E0 k6=0 Wave function ϕ(2) = R̂0 V̂ R̂0 V̂ ψ (1) + R̂0 E (1) R̂0 V̂ ψ (0) = = R̂0 V̂ R̂0 V̂ ϕ0 − R̂0 hV̂ iR̂0 V̂ ϕ0 = R̂0 V R̂0 V̂ ϕ0 where we used the definitions hV̂ i = hϕ0 |V̂ |ϕ0 i J. Ángyán (EMQC) and IMF V = V̂ − hV̂ i 121 / 201 Third order ∆E (3) = hϕ0 |V̂ |ψ (2) i = −hϕ0 |V̂ R̂0 V R̂0 V̂ |ϕ0 i X X hϕ0 |V̂ |ϕk ihϕk |V |ϕl ihϕl |V̂ |ϕ0 i = (Ek − E0 )(El − E0 ) k6=0 l6=0 J. Ángyán (EMQC) IMF 122 / 201 Summary of energy corrections ∆E (1) = hV̂ i ∆E (2) = hV̂ R̂0 V̂ i ∆E (3) = hV̂ R̂0 V R̂0 V̂ i ” “ ∆E (4) = hV̂ R̂0 V R̂0 V − hV R̂0 V i R̂0 V̂ i ∆E (5) = hV̂ R̂0 (V R̂0 V R̂0 V − hV R̂0 V R̂0 V i − V R̂0 hV R̂0 V i − hV R̂0 V iR̂0 V )R̂0 V̂ i J. Ángyán (EMQC) IMF 123 / 201 Energy with the first-order wave function The energy (Rayleigh quotient) E= hψ|Ĥ + λV̂ |ψi hψ|ψi with the first order wave function, ψ = ϕ0 − λR̂0 V̂ ϕ0 E= hϕ0 − λϕ0 V̂ R̂0 |Ĥ + λV̂ |ϕ0 − λR̂0 V̂ ϕ0 i 1 + λ2 hϕ0 V̂ R̂0 |R̂0 V̂ ϕ0 i After expanding the denominator and using that R̂0 Ĥ0 ϕ0 = 0 ` E = E0 + λE (1) − 2λ2 hϕ0 |V̂ R̂0 V̂ |ϕ0 i+ ´ + λ2 hϕ0 |V̂ R̂0 (Ĥ + λV̂ )R̂0 V̂ |ϕ0 i × ` ´ × 1 − λ2 hϕ0 V̂ R̂0 |R̂0 V̂ ϕ0 i J. Ángyán (EMQC) IMF 124 / 201 and collecting terms of the same order E = E0 + λE (1) − − λ2 2hϕ0 |V̂ R̂0 V̂ |ϕ0 i− − λ2 hϕ0 |V̂ R̂0 (Ĥ − E0 )R̂0 V̂ |ϕ0 i + λ3 hϕ0 |V̂ R̂0 (V̂ − E (1) )R̂0 V̂ |ϕ0 i Use that E (1) = hV̂ i and R̂0 (Ĥ − E0 ) = 1 − |ϕ0 ihϕ0 | and obtain the previously derived 3rd order energy expression E = E0 + hϕ0 |V̂ |ϕ0 i − hϕ0 |V̂ R̂0 V̂ |ϕ0 i + hϕ0 |V̂ R̂0 (V̂ − hV̂ i)R̂0 V̂ |ϕ0 i This result can be generalized: the nth order wave function determines the (2n+1)th order energy expression, provided the normalization is taken into account. This is Wigner’s (2n + 1) theorem. J. Ángyán (EMQC) IMF 125 / 201 Deformation energy and perturbation energy Up to second order the Rayleigh quotient can be written as a sum of two terms, the expectation value of the zero order Hamiltonian hϕ − λϕV̂ R̂0 |Ĥ|ϕ − λR̂0 V̂ ϕi (2) = E0 + λ2 hϕ|V̂ R̂0 V̂ |ϕi = E0 + ∆Edef 1 + λ2 hϕV̂ R̂0 |R̂0 V̂ ϕi and the expectation value of the perturbation operator hϕ − λϕV̂ R̂0 |λV̂ |ϕ − λR̂0 V̂ ϕi (2) = λhϕ|V̂ |ϕi − λ2 2hϕ|V̂ R̂0 V̂ |ϕi = E (1) + ∆Estab 1 + λ2 hϕV̂ R̂0 |R̂0 V̂ ϕi The second order correction to the expectation value of the perturbation is twice the second order energy correction and it is twice the energy raise of the wave function due to the deformation of the wave function. (2) (2) ∆Estab = −2∆Edef (2) (2) ∆E (2) = ∆Estab − ∆Edef = J. Ángyán (EMQC) IMF 1 (2) ∆Estab 2 126 / 201 Molecule in external potential In first order of the perturbation theory ∆E (1) = hψ0 |q̂|ψ0 i · V0 + hψ0 |µ̂α |ψ0 i · Fα = qV0 + Fα µα one retrieves the classical charge-potential and dipole-field interactions. In second-order of the perturbation theory ∆E (2) = −hψ0 |V̂ R̂0 V̂ |ψ0 i = − X hψ0 |V̂ |ψk ihψk |V̂ |ψ0 i Ek − E0 k6=0 The matrix elements hψ0 |q̂|ψk i = 0, since the eigenstates are orthogonal. Only the dipolar term survives X ∆E (2) = − Fα hψ0 |µ̂α R̂0 µ̂β |ψ0 iFβ αβ Using the definition of the dipolar linear response function (polarizability) ∆E (2) = − 1 X Fα ααβ Fβ 2 αβ J. Ángyán (EMQC) IMF 127 / 201 In third order of the perturbation theory ∆E (3) = −hψ0 |V̂ R̂0 V R̂0 V̂ |ψ0 i Insert the interaction operator, and remember that V = V̂ − hV̂ i, X ∆E (3) = − Fα Fβ Fγ × αβγ X X hψ0 |µ̂α |ψk ihψk |µ̂β |ψl ihψl |µ̂γ |ψ0 i − (Ek − E0 )(El − E0 ) k6=0 l6=0 X hψ0 |µ̂α |ψk ihψk |µ̂γ |ψ0 i ff hψ0 |µ̂β |ψ0 i = (Ek − E0 )2 k6=0 1X =− Fα Fβ Fγ βαβγ 6 αβγ where βαβγ is the first dipolar hyperpolarizability (non-linear response function). J. Ángyán (EMQC) IMF 128 / 201 Multipole polarizabilities Dipole polarizability is a symmetric tensor 0 αxx α=@ αxy αyy 1 αxz αyz A αzz The SI units of polarizability are Farad m2 , or equivalently, C2 m2 J−1 or C m2 V−1 . Other units are volume (Å3 or bohr3 ). 1 a.u. = bohr3 = 0.148185 Å3 = 0.16488×10−40 Farad m2 . 1 C2 m2 J−1 = 0.8988×1016 cm3 =6.065 ×1040 a.u. Proportional to the volume, as it can be seen by introducing an average excitation energy and using the resolution of identity for the polarizability of a one-electron system α= ´ 1 X 2h0|r̂α |nihn|r̂α |0i 2 ` ≈ h0|r̂2 |0i − h0|r̂α |0ih0|r̂α |0i 3 ∆E0n 3U n6=0 and inversely proportional to the excitation energy. J. Ángyán (EMQC) IMF 129 / 201 As any second-rank tensor, it can be decomposed into irreducible parts, according to α = α(0) + α(1) + α(2) where (0) 1 Tr(α)δαβ 3 1 = (ααβ − αβα ) = 0 2 1 1 = (ααβ + αβα ) − Tr(α)δαβ 2 3 ααβ = (1) ααβ (2) ααβ α(1) vanishes, since α is symmetric. In a principal-axis system we have the decomposition 0 1 0 1 α 0 0 αxx − α 0 0 0 αyy − α 0 A α = @0 α 0A + @ 0 0 α 0 0 αzz − α J. Ángyán (EMQC) IMF 130 / 201 The first trace-invariant quantity that can be formed is the mean polarizability α= 1 1 Trα = (αxx + αyy + αzz ) 3 3 and the second trace-invariant is the polarizability anisotropy, γ, defined as the positive root of 1 γ 2 = [3Tr(α2 ) − Tr(α)2 ] 2 or in components 1 γ 2 = [3ααβ αβα − ααα αββ ] 2 which can be written in a principal axis system γ2 = 1 [(αxx − αyy )2 + (αyy − αzz )2 + (αzz − αxx )2 ] 2 and makes clear that this quantity vanishes for spherically symmetric systems. For linear molecules αzz = αk and αxx = αyy = α⊥ and the polarizability anisotropy, γ γ = αk − α⊥ J. Ángyán (EMQC) IMF 131 / 201 Translation of polarizabilities The dipole-dipole polarizability is always origin-independent. Higher-rank multipole polarizabilities are (always) origin-dependent. For instance, the Az,zz component involves the Θ̂zz operator. After a shift of the origin by c = (0, 0, c) O O Θ̂C zz = Θ̂zz − 2cµ̂z and the dipole-quadrupole polarizability at the new origin is AC z,zz = O O X h0|µ̂O z |nihn|Θ̂zz − 2cµ̂z |0i = AO z,zz − 2cαzz ∆E0n n6=0 This means that the origin (and the dipole polarizability) should always be specified when Aα,βγ is given. J. Ángyán (EMQC) IMF 132 / 201 Spherical harmonic polarizabilities The general multipole polarizabilities, defined in terms of the (irreducible) multipole moment operators, Q̂`m α`1 m1 ,`2 m2 = X h0|Q̂` m |nihn|Q̂` m |0i + h0|Q̂` m |nihn|Q̂` m |0i 1 1 2 2 2 2 1 1 ∆E0n n6=0 is a reducible spherical tensor quantity, which can be decomposed into irreducible parts as X α`1 `2 :kq = C(`1 `2 k; m1 m2 q)α`1 m1 ,`2 m2 m1 m2 where C(`1 `2 k; m1 m2 q) are the Clebsch-Gordan coefficients. Since C = 0, unless k = `1 + `2 , `1 + `2 − 1, . . . , |`1 − `2 |, the nonzero irreducible parts of the dipole-dipole polarizability can be only with k = 0, 2, for the dipole-quadrupole polarizability, k = 1, 3, etc. For instance, r 1 α11:00 = (αxx + αyy + αzz ) 3 r 2 α11:20 = γ 3 J. Ángyán (EMQC) IMF 133 / 201 Induction energy Consider a potential and its derivatives created by a molecule A at the center of molecule B. The corresponding perturbation energy will be induction energy. At the second order: Taking into account that hψ0B |q̂ B |ψbB i = 0, one has the leading terms of the induction energy: E (2) (ind,B) = B X h0|µ̂B α |bihb|µ̂α0 |0i − (Tα q A − Tαβ µA (Tα0 q A − Tα0 β 0 µA α + . . .) α0 + . . .)− B ∆E 0b b6=0 B X h0|Θ̂B αβ |bihb|µ̂α0 |0i − (Tαβ q A + Tαβγ µA (Tα0 q A − Tα0 β 0 µA γ + . . .) β 0 + . . .)− B ∆E 0b b6=0 B X h0|µ̂B α |bihb|Θ̂α0 β 0 |0i (Tα0 β 0 q A + Tα0 β 0 γ 0 µA − (Tα q A − Tαβ µA α + . . .) γ + . . .)− B ∆E 0b b6=0 B X h0|Θ̂B αβ |bihb|Θ̂α0 β 0 |0i (Tα0 β 0 q A − Tα0 β 0 γ 0 µA − (Tαβ q A + Tαβγ µA γ 0 + . . .) . . . γ 0 + . . .) B ∆E 0b b6=0 J. Ángyán (EMQC) IMF 134 / 201 Introduce the multipole polarizabilities ααβ = X h0|µ̂α |nihn|µ̂β |0i + h0|µ̂β |nihn|µ̂α |0i ∆E0n n6=0 Aα,βγ X h0|µ̂α |nihn|Θ̂βγ |0i + h0|Θ̂βγ |nihn|µ̂α |0i = ∆E0n n6=0 Cαβ,γδ = 1 X h0|Θ̂αβ |nihn|Θ̂γδ |0i + h0|Θ̂γδ |nihn|Θ̂αβ |0i 3 ∆E0n n6=0 and identify the parentheses as the electric field, field gradient, etc. FαA = −(Tα q A − Tαβ µA α + . . .) A Fαβ = −(Tαβ q A + Tαβγ µA γ + . . .) The induction energy in terms of the field (and its gradients) and the multipolar polarizabilities 1 A B 1 A B 1 B A 0 Fα0 − E (2) (ind,B) = − FαA αα,α Fα Aα,α0 β 0 FαA0 β 0 − Fαβ Cαβ,α0 β 0 FαA0 β 0 + . . . 2 3 6 J. Ángyán (EMQC) IMF 135 / 201 Induction energy - spherical tensor components In the spherical tensor formalism, the general polarizability component α`κ,`0 κ0 = X h0|Q̂`κ |nihn|Q̂`0 κ0 |0i + h0|Q̂`0 κ0 |nihn|Q̂`κ |0i ∆E0n n6=0 and the induction energy takes the form E (2) (ind,B) = − 1 XX B 1X A A A α`κ`0 κ0 V`κ ∆QB V`0 κ0 = − `κ` V`κ 2 2 0 0 `κ ` κ `κ where ∆QB `κ` are the induced moments of B X B ∆QB α`κ`0 κ0 VÀ0 κ0 `κ = `0 κ0 J. Ángyán (EMQC) IMF 136 / 201 Truncation of the multipolar induction energy The multipolar induction energy can be truncated according to the powers of (1/R)N does not ensure that the induction energy is negative according to the maximum rank of the multipole operators (L) always negative J. Ángyán (EMQC) IMF 137 / 201 Distance dependence of the induction energy Interaction of a spherically symmetric polarizability ααβ = αδαβ with multipoles: charge 2 1 1 q2 α 1 1 X αRα E(ind, q) = − qTα ααβ Tβ q = − q 2 Tα Tα α = − q 2 =− 3 3 2 2 2 R R 2 R4 α dipole 1 µ2 α(3 cos2 θ + 1) 1 E(ind, µ) = − µα Tαβ αββ 0 Tβ 0 α0 µα0 = − 2 2 R6 quadrupole E(ind, Θ) ∼ R−8 J. Ángyán (EMQC) IMF 138 / 201 Convergence of the induction energy The multipole-expanded interaction Hamiltonian of a H-atom + proton system is » «n – ∞ „ X r 1 1− Pn (cos θ) Vmult = R R n=0 The exact second order multipole energy (Dalgarno & Lynn, 1957) E (2) = − ∞ X (2n + 2)!(n + 2) n(n + 1)R(2n+2) n=1 The ratio of successive terms lim n→∞ 2n(n + 3)(2n + 3) =∞ (n + 2)R2 indicates that for any value of R the series is divergent. J. Ángyán (EMQC) IMF 139 / 201 Non-additivity of the induction energy charge-polarizability interaction 1 1 q2 Uqα = − αF 2 = − α 4 2 2 R two charges of opposite signs: F is doubled U{q1 +q2 }α = 4Uqα 6= Uq1 α + Uq2 α two charges of the same sign: F is zero U{q1 +q2 }α = 0 6= Uq1 α + Uq2 α this effect explains the arrangement of Mg2+ cations (and other alkaline earth cations) around the polarizable Cl− anions in crystal and molten phases: induction effects arising with an angle Mg-Cl-Mg < 180 effectively reduce the cation-cation repulsion. If the anion is not large enough (F−) this phenomenon does not take place. J. Ángyán (EMQC) IMF 140 / 201 Cooperativity of induction Interaction of polarizable particles enhance the overall polarization effect. The induced dipoles p1 and p2 are obtained from the total local fields ´ ` p1 = α1 F 1 = α1 E + T 12 · p2 ` ´ p2 = α2 F 2 = α2 E + T 21 · p1 The solution of this coupled system of equations: „ « „ −1 «−1 „ « p1 α1 −T E = E p2 −T α−1 2 The effective polarizability is: „ 1 α1 α1 α2 T 1 − T 2 α1 α2 J. Ángyán (EMQC) α1 α2 T α2 « IMF 141 / 201 Part V Charge fluctuation interactions J. Ángyán (EMQC) IMF 142 / 201 Thermally averaged interactions Thermal average of orientation-dependent interactions U (Ω), where Ω = (θ, φ) R dΩU (Ω)e−U (Ω)/kT hUqµ i = R dΩe−U (Ω)/kT  cosn θ = 2 = U − (U 2 /kT − U /kT ) + . . . where Z dΩU n (Ω) = J. Ángyán (EMQC) ZZ 1 , 2k+1 n = 2k + 1; n = 2k. cosn φ = Expand the exponential (U (Ω)/kT 1): R dΩ(U (Ω) − U 2 (Ω)/kT + . . .) R hUqµ |i ≈ dΩ(1 − U (Ω)/kT + . . .) ` ´` ´ 2 = U − U 2 /kT 1 + U /kT Un = 0, U n (θ, φ) sin θdθdφ IMF sinn φ = k 1 2 3 4  0, cos2k θ 1/3 1/5 1/7 1/9 (2k−1)!! , 2k k! n = 2k + 1; n = 2k. sin2k θ 2/3 8/15 16/35 128/315 cos2k φ 1/2 3/8 5/16 35/128 143 / 201 Charge-dipole interaction Charge-dipole interaction Uqµ = qA µB cos θ R2 Thermal averages qµ cos θ = 0 R2 2 2 q µ 1 q 2 µ2 = cos2 θ = 4 R 3 R4 U qµ = U 2 qµ Analogous to the charge-polarizability interaction: hUqµ i = − J. Ángyán (EMQC) IMF 1 q 2 µ2 3kT R4 144 / 201 Dipole-dipole (Keesom) interaction Dipole-dipole interaction Uµµ = − ´ µA µB ` 2 cos θA cos θB − sin θA sin θB cos ϕ 2 R Thermal average hUµµ i = −U 2 µµ /kT ´ 1 µ2A µ2B ` 4 cos2 θA cos2 θB − sin2 θA sin2 θB cos2 ϕ + cross terms 6 kT R 1 µ2A µ2B ` 1 1 2 2 1´ 2 µ2A µ2B 4× × − × × =− =− kT R6 3 3 3 3 2 3kT R6 U 2 µµ = − Keesom forces: 2 µ2A µ2B 3kT R6 Correlation of thermal fluctuations give rise to universally attractive interactions. hUµµ i = − J. Ángyán (EMQC) IMF 145 / 201 London dispersion forces Edisp = − 1 2π Z dω α1 (r1 , r10 |iω) T (r1 , r2 ) α2 (r2 , r20 |iω) T (r20 , r10 ) universally attractive always attractive and decays as R−6 long-range dynamical correlation J. Ángyán (EMQC) IMF 146 / 201 London dispersion forces Edisp = − 1 2π Z dω α1 (r1 , r10 |iω) T (r1 , r2 ) α2 (r2 , r20 |iω) T (r20 , r10 ) universally attractive always attractive and decays as R−6 long-range dynamical correlation J. Ángyán (EMQC) IMF 146 / 201 London dispersion forces -3 R Edisp = − 1 2π Z dω α1 (r1 , r10 |iω) T (r1 , r2 ) α2 (r2 , r20 |iω) T (r20 , r10 ) universally attractive always attractive and decays as R−6 long-range dynamical correlation J. Ángyán (EMQC) IMF 146 / 201 London dispersion forces -3 R Edisp = − 1 2π Z dω α1 (r1 , r10 |iω) T (r1 , r2 ) α2 (r2 , r20 |iω) T (r20 , r10 ) universally attractive always attractive and decays as R−6 long-range dynamical correlation J. Ángyán (EMQC) IMF 146 / 201 London dispersion forces -3 R R Edisp = − 1 2π Z -3 dω α1 (r1 , r10 |iω) T (r1 , r2 ) α2 (r2 , r20 |iω) T (r20 , r10 ) universally attractive always attractive and decays as R−6 long-range dynamical correlation J. Ángyán (EMQC) IMF 146 / 201 Long-range intermolecular RSPT The solution of the Schrödinger equation for the non-interacting complex “ ” Ĥ A + Ĥ B ϕk = E0 ϕk can be obtained from the solutions of the isolated subsystem Schrödinger equations Ĥ A ψaA = EaA ψaA Ĥ X = X i∈X X Zα T̂i − riα α∈X Ĥ B ψbB = EbB ψbB ! + X i,j∈X i<j X Zα Z α 0 1 + rij Rαα0 a,b∈X α<α0 as simple products (not antisymmetric for intermolecular electron exchange) of the monomer wave functions ϕk = ψaA ψbB and the eigenvalues are the sum of monomer eigenvalues Ek = EaA + EbB J. Ángyán (EMQC) IMF 147 / 201 Partition of the Hamiltonian Since the subsystems are distinguishable (preserve their identities), each of the N = NA + NB electrons and M = MA + MB nuclei can be assigned to one of the subsystems. Subtracting from the total Hamiltonian ! MA +MB NA +NB NA +NB MA +MB X Zα X X Zα Z α 0 1 X 1 T̂i − Ĥ = + + r 2 r Rαα0 iα ij α=1 i=1 i,j=1 α,β=1 the sum of monomer Hamiltonians one obtains the operator of the intermolecular interaction X X Zα Zβ X X Zβ X X Za XX 1 V̂ = − − + Rαβ riβ α∈A j∈B rαj i∈A j∈B rij α∈A i∈A β∈B β∈B In the absence of any “natural” perturbation parameter, we shall consider an adiabatic switching of the interaction between the subsystems: Ĥ(λ) = Ĥ A + Ĥ B + λV̂ J. Ángyán (EMQC) IMF 148 / 201 Longuet-Higgins form of the interaction operator The interaction operator can be written in a more compact and separable form, based on the charge density operator, defined as X X %̂X (r) = Zα δ(r − Rα ) − δ(r − r i ) α∈X i∈X with the matrix elements hψa |%̂A (r)|ψa0 i = δaa0 X Zα δ(r − Rα ) − P (aa0 |r, r 0 ) α∈X where P (aa0 |r, r 0 ) is an element one the one particle density matrix. J. Ángyán (EMQC) IMF 149 / 201 The state charge density %aa (r) = X Zα δ(r − Rα ) − P (aa|r, r) α∈X contains the contribution of both electrons and nuclei. Transition charge density %aa0 (r) = −P (aa0 |r, r) Using %̂(r) and the Coulomb-kernel function, T (r, r 0 ) = |r − r 0 |, the interaction operator is Z Z V̂ = dr dr 0 %̂A (r)T (r, r 0 )%̂B (r 0 ) By a straightforward generalization of the Einstein summation convention B V̂ = %̂A r Tr,r 0 %̂r 0 J. Ángyán (EMQC) IMF 150 / 201 The polarization approximation Direct application of the RSPT to the the above problem with the eigenfunction of Ĥ0 = HÂ + ĤB as zeroth order wave function: (n) (n−1) Epol = hϕ0 |V̂ |ϕpol (n) (n−1) ϕpol = −R̂0 V̂ ϕpol − n−1 X i (n−k) ∆E (k) R̂0 ϕpol k=1 This is called the polarization approximation (antisymmetry requirement neglected). J. Ángyán (EMQC) IMF 151 / 201 First order: electrostatic energy The first-order interaction energy in this approximation is (1) Epol = hψ0A ψ0B |V̂ |ψ0A ψ0B i Using the Longuet-Higgins operator Z Z (1) Epol = dr dr 0 hψ A |%̂A (r)|ψ A iT (r, r 0 )hψ B |%̂B (r 0 )|ψ B i it is easy to see that it is the Coulomb interaction of the charge densities of the two subsystems. Z Z (1) 0 B 0 Epol = dr dr 0 %A 00 (r)T (r, r )%00 (r ) Electrostatic potential of the subsystems Z 0 V A (r) = dr 0 T (r, r 0 )%A 00 (r ) V B (r) = Z 0 dr 0 T (r, r 0 )%B 00 (r ) Alternative form of the first order interaction energy Z Z (1) B A Epol = dr%A (r)V (r) = dr%B 00 00 (r)V (r) J. Ángyán (EMQC) IMF 152 / 201 Second order energy in the polarization approximation The second-order interaction energy (2) Epol = − X |hψ0A ψ0B |V̂ |ψaA ψ B i|2 b A B ∆E + ∆E 0a 0b ab6=00 can be written as a sum of three terms, each having a different physical meaning. Epol = − X |hψ0A ψ0B |V̂ |ψ0A ψ B i|2 b B ∆E 0b b6=0 induction A → B − X |hψ0A ψ0B |V̂ |ψaA ψ0B i|2 A ∆E0a a6=0 induction A ← B − X |hψ0A ψ0B |V̂ |ψaA ψ B i|2 b A B ∆E + ∆E 0a 0b a6=0 dispersion (2) b6=0 These terms correspond to the following decomposition of the reduced resolvent R̂0 = X a,b (ab)6=(00) |ψaA ψbB ihψaA ψbB | = R0A OA + R0B OB + R0AB = R0 (ind) + R0 (disp) EaA − E0A + EaB − E0B J. X Ángyán (EMQC) X X IMF 153 / 201 Induction energy ∆E (2) (ind, A ← B) = −hψ0A ψ0B |V̂ R̂0A ÔB V̂ |ψ0A ψ0B i 1 B A B A A B = −VrB h%A r R̂0 %r 0 iVr = − Vr K(%r , %r 0 )Vr 2 0 A The K(%A r , %r 0 ) = α(r, r ; ω = 0) charge density linear response function (susceptibility) is a kind of generalized polarizability function, which gives the induced charge density in a static external potential Z ∆%A (r) = dr 0 α(r, r 0 ; ω = 0)V B (r 0 ) The sum-over-states definition of the charge density susceptibility at the ω frequency is α(r, r 0 ; ω) = 1 X [h0|%̂(r)|aih0|%̂(r 0 )|ai + h0|%̂(r 0 )|aih0|%̂(r)|ai] ω0a 2 ~ ω0a − ω2 a6=0 J. Ángyán (EMQC) IMF 154 / 201 The induction energy can be regarded as the stabilization energy due to interaction of the induced charge density with the electrostatic potential of the partner Z (2) ∆Estab = − dr∆%A (r)V B (r) partially compensated by the (positive) deformation energy, spent to polarize the charge distribution 1 (2) (2) ∆Edef = − ∆Estab 2 Which means that the induction energy (2) (2) ∆E (2) (ind, A ← B) = ∆Estab + ∆Edef = 1 (2) ∆Estab 2 is the half of the stabilization energy (in the linear response approximation). Note: do not mix up the terminology “polarization” and “induction”... J. Ángyán (EMQC) IMF 155 / 201 Dispersion energy ∆E (2) (disp) = −hψ0A ψ0B |V̂ R̂0AB V̂ |ψ0A ψ0B i ZZZZ A 0 B B 0 1 X X %A 0a (r)%0a (r )%0b (s)%0b (s ) = T (r, s)T (r 0 , s0 ) A B ~ ω0a + ω0b a6=0 b6=0 We can transform the double sum according to subsystems using the following identity Z 1 2 ∞ x y = dω x+y π 0 x2 + ω 2 y 2 + ω 2 which leads to a separable form at the expense of an additional integral in the frequency domain ZZZZ ∆E (2) (disp) = T (r, s)T (r 0 , s0 )× Z A A 0 X B B 0 %0a (r)%A ω0b %0b (s)%B 2 1 X ω0a 0a (r ) 0b (s ) dω A2 B2 π ~ ω0a + ω2 ω0b + ω2 b6=0 a6=0 J. Ángyán (EMQC) IMF 156 / 201 Dispersion energy We can recognize in the two separate sums the dynamic charge density susceptibilities at imaginary frequencies of both subsystems, i.e. α(r, r 0 ; iω) = 1 X [h0|%̂(r)|aih0|%̂(r 0 )|ai + h0|%̂(r 0 )|aih0|%̂(r)|ai] ω0a 2 ~ ω0a + ω2 a6=0 Final expression of the dispersion energy (Casimir-Polder) Z ∞ ZZZZ ~ dω drdr 0 dsds0 × ∆E (2) (disp) = 2π 0 × αA (r, r 0 ; iω)T (r 0 , s0 )αB (s, s0 ; iω)T (r, s) Corresponds to the Coulomb correlation of fluctuating charge densities of the two systems. (Cf. fluctuation-dissipation theorem). J. Ángyán (EMQC) IMF 157 / 201 Summary of second order terms B %A r Trs %s electrostatic J. Ángyán (EMQC) B A B A %A r Trs αss0 Ts0 r0 %r0 Trs αss0 Ts0 r0 αr0 r induction IMF dispersion 158 / 201 Third order induction energy Third order energy ∆E (3) = ϕ0 |V̂ R̂0 (V̂ − hV̂ i)R̂0 V̂ |ϕ0 i Decomposition of the reduced resolvent R0 (ind) = R0A OB + OA R0B R0 (disp) = R0AB Pure induction part of the third order energy can be expanded h i ∆E (3) (ind) = hϕ0 |V̂ R̂0 (ind) V̂ − hV̂ i R̂0 (ind)V̂ |ϕ0 i = Trs Tr0 s0 Tr00 s00 × h i B A B A B A B A B A B hϕA 0 ϕ0 |%̂r %̂s R̂0 (ind) %̂r %̂s − h%̂r 0 %̂s0 i R̂0 (ind) %̂r 00 %̂s00 |ϕ0 ϕ0 i J. Ángyán (EMQC) IMF 159 / 201 Two kinds of terms are obtained hyperpolarizability term (nonlinear response), e.g. A A B B B B B B Trs Tr0 s0 Tr00 s00 h%̂A r ih%̂r 0 ih%̂r 00 i h%̂s R̂0 (%̂s0 − h%̂s0 i)R̂0 %̂s00 i | {z } 1 β B (s,s0 ,s00 ) 6 iterated linear response terms, e.g. B B B A A A B Trs Tr0 s0 Tr00 s00 h%̂A r i h%̂s R̂0 %̂s0 i h%̂r 0 R̂0 %̂r 00 ih%̂s00 i {z } | {z } | 1 αB (s,s0 ) 2 1 αA (r 0 ,r 00 ) 2 Graphical representation of the iterated linear response terms J. Ángyán (EMQC) IMF 160 / 201 Analogous terms appear in higher order terms, that can be iterated up to self-consistency J. Ángyán (EMQC) IMF 161 / 201 The Hamiltonian operator of a ternary complex ĤA + ĤB + ĤC + V̂AB + V̂AC + V̂BC is "additive". First order energy is strictly additive (1) ∆EABC = hψ A ψ B ψ C |V̂AB + V̂AC + V̂BC |ψ A ψ B ψ C i = hψ A ψ B |V̂AB |ψ A ψ B ihψ C |ψ C i+ + hψ A ψ C |V̂AC |ψ A ψ C ihψ B |ψ B i+ + hψ B ψ C |V̂BC |ψ B ψ C ihψ A |ψ A i (2) (2) (2) = ∆EAB + ∆EAC + ∆EBC Second order energy (2) ∆EABC = hψ A ψ B ψ C |(V̂AB + V̂AC + V̂BC )R̂0 (V̂AB + V̂AC + V̂BC )|ψ A ψ B ψ C i The resolvent can be decomposed as R̂0 = R̂0ABC +R̂0AB ÔC + R̂0BC ÔA + R̂0CA ÔB +R̂0A ÔB ÔC J. Ángyán (EMQC) + R̂0B ÔC ÔA + R̂0C ÔA ÔB IMF 2-body dispersion induction 162 / 201 Three types of contributions according to the interaction operators "Diagonal" term hψ A ψ B ψ C |V̂AB R̂0 V̂AB |ψ A ψ B ψ C i = hψ A ψ B |V̂AB hψ C |R̂0 |ψ C iV̂AB |ψ A ψ B i = (2) hψ A ψ B |V̂AB (R̂0AB + R̂0A ÔB + R̂0B ÔA )V̂AB |ψ A ψ B i = ∆EAB "Off-diagonal" term hψ A ψ B ψ C |V̂AB R̂0 V̂AC |ψ A ψ B ψ C i = hψ A ψ B |V̂AB hψ C |R̂0 |ψ B iV̂AC |ψ A ψ C i = hψ A ψ B |V̂AB |ψ B iR̂0A hψ C |V̂AC |ψ A ψ C i = A A A C Trs Tr0 s0 %B s h%̂r R̂0 %̂r 0 i%s0 non-additive 3-body induction interaction. J. Ángyán (EMQC) IMF 163 / 201 London dispersion energy Dispersion interaction energy in spherical tensor formalism XX X X E (2) (disp) = − a6=0 b6=0 À mA `B mB × B A B h00|Q̂A À mA TÀ mA ,`B mB Q̂`B mB |abihab|Q̂`0 m0 T`0A m0A ,`0B m0B Q̂`0 m0 |00i A A B B A B ∆E0a + ∆E0b Applying the Casimir-Polder method 2 T` m ,` m T 0 0 0 0 × ~π A A B B À mA ,`B mB A A B B ∞ h0|Q̂ ∞ X À mA |aiha|Q̂`0 m0 |0iω0a X h0|Q̂`B mB |bihb|Q̂`0 E (2) (disp) = − Z × dω A a6=0 J. Ángyán (EMQC) 2 ω0a + A B ω2 b6=0 IMF 2 ω0b + m0B |0iω0b ω2 164 / 201 Dynamic (frequency-dependent) multipole polarizabilities in molecule-fixed frame α`m,`0 m0 (ω) = X 2ω0n h0|Q̂`m |aiha|Q̂`0 m0 |0i 2 ω0a − ω2 n6=0 related to the charge density susceptibility ZZ 0 0 α`m,` m (ω) = drdr 0 R`m (r)α(r, r 0 |ω)R`0 m0 (r 0 ) Dispersion energy E (2) (disp) = − J. Ángyán (EMQC) X 0 TÀ mA ,`B mB T`0A m0A ,`0B m0B XÀB A mA `B mB ` A IMF m0A ,`0B m0B 165 / 201 The Casimir-Polder or dispersion integrals are defined as Z ~ 0 m0 ,`0 = XÀB dωαÀA mA ,`0 m0 (iω)α`BB mB ,`0 m0 (iω) m ` m ` A A B B A A B A A B B 2π The dispersion integrals can be calculated by numerical quadrature as X AB = M ~ X w(ωj )αA (iωj )αB (iωj ) 2π j=1 With a Gauss-Chebyshev quadrature scheme the grid points are chosen as „ « 2j − 1 ωj = cot π 4M and the weights w(ωj ) = 2π 4M sin2 (π(2j − 1)/4M ) Typically, with 5 and 7 grid points one has an accuracy of 0.1 %. J. Ángyán (EMQC) IMF 166 / 201 Numerically more efficient procedure (for high-rank calculations) is to contract first the polarizabilities with the interaction tensors (in local frame) and perform the numerical integration afterwards (Hättig, 1996). In this form the interaction tensors and X AB are both reducible: they transform according to the double and quadruple product group of SO(3). In terms of irreducible tensors, the dispersion coefficients are of the form (Wormer) X X BL 0 0 0 0 · factor C`LA`L XÀB 0 ` `0 = A mA `B mB ` m ,` m A A B B A mA m0A mB m0B A B B The algebraic factor depends on the Wigner 3j and 9j coefficients. These coefficients are coupled to the following form CnLA LB L (n = À + `B + `0A + `0B + 2) For atoms in S-state, for example, (2) Edisp = − ∞ X C2n R−2n n=3 C2n = n−2 X C(`; n − k − 1) `=1 C(`; `0 ) = J. Ángyán (EMQC) (2` + 2`0 )! 1 (2`)!(2`0 )! 2π IMF Z dωαÀ (iω)α`B0 (iω) 167 / 201 The dispersion integral depends on the properties of the individual molecules and independent of the intermolecular geometry. The complete expression can be expressed in terms of irreducible spherical tensor components. dipole-dipole leading term R−3 R−3 ∼ R−6 dipole-quadrupole would be R−3 R−4 ∼ R−7 , after averaging over all orientations, it gives zero quadrupole-quadrupole term R−4 R−4 ∼ R−8 dipole-octopole and quadrupole-qudrupole R−10 J. Ángyán (EMQC) IMF 168 / 201 Dipolar dispersion energy The leading multipolar term in the dispersion interaction energy E (2) (disp) = − B A B X X h00|µ̂A α Tαβ µ̂β |abihab|µ̂γ Tγδ µ̂δ |00i A B ∆E0a + ∆E0b a6=0 b6=0 Casimir-Polder formula E (2) (disp) = −Tαβ Tγδ 2 ~π Z dω ∞ ∞ h0|µ̂B |bihb|µ̂B |0iω A X X h0|µ̂A 0b α |aiha|µ̂γ |0iω0a β δ 2 + ω2 ω0a a6=0 b6=0 2 + ω2 ω0b Unsöld approximation E (2) (disp) = −Tαβ Tγδ J. Ángyán (EMQC) ∞ X ∞ A ∆E B X ∆E0a 0b A ∆E0a a6=0 b6=0 + IMF B ∆E0b B B A h0|µ̂A α |aiha|µ̂γ |0i h0|µ̂β |bihb|µ̂δ |0i A ω0a B ω0b 169 / 201 In order to factor this latter expression, we use the identity A B ∆E0a ∆E0b UA UB = (1 + ∆ab ) A B UA + UB ∆E0a + ∆E0b with ∆ab = A B 1/UA − 1/E0a + 1/UB − 1/E0b A B 1/E0a + 1/E0b that can be made negligibly small by choosing appropriate average excitation energies UA and UB UA UB A B E (2) (disp) ≈ − Tαβ Tγδ ααγ αβδ 4(UA + UB ) J. Ángyán (EMQC) IMF 170 / 201 In both expressions we can separate the orientation-independent spherically averaged and various orientation-dependent components, by using the decomposition of the polarizabilities to irreducible parts. The spherically averaged component becomes in both cases 6 Tαβ Tγδ αA δαγ αB δβδ = αA αB Tαβ Tαβ = αA αB 6 R leading to the general expression E (2) (disp) ≈ − C6 R6 with the C6 coefficient Z C6 = 3~ C6 ≈ J. Ángyán (EMQC) dωαA (iω)αB (iω) 3UA UB αA αB 2(UA + UB ) IMF (Casimir-Polder) (London) 171 / 201 Experimental oscillator strength distributions can be used to determine “experimental” C6 coefficients. Roughly proportional to the square of the polarizability/volume. Some typical values system H· · · H He· · · He Ne· · · Ne Ar· · · Ar Kr· · · Kr Xe· · · Xe C6 6.5 1.46 6.6 64.3 133 286 C8 124.4 13.9 57 1130 2500 C10 1135 182 700 25000 60000 Combining rules can be deduced from the London-formula q C6AB ≈ C6AA C6BB J. Ángyán (EMQC) IMF 172 / 201 Approximate dispersion energy The average excitation energy of the London formula is an empirical parameter, either the first ionization potential (quite bad) or the first excitation energy (somewhat better) is used. Similar expressions can be derived from the Casimir-Polder expression, by considering some general properties of the average dynamic dipole-dipole polarizabilities α(iω) = 1 X 2ω0k |h0|x̂|ki|2 2 ~ ω0k + ω2 k6=0 We are looking for the simplest, one-term approximation in the form α(iω) ≈ ω2 ·a ω2 + ω2 Parameters a and ω will be found from the asymptotic behaviour of α(iω). J. Ángyán (EMQC) IMF 173 / 201 For ω = 0 one gets the static polarizability, a = α(0). For ω → ∞ one gets the Thomas-Reiche-Kuhn sum rule, the number of electrons α(iω) → 1 X ~2 ω 2 n6=0 2∆E0n x20n = n ~2 ω 2 In this limit we have a n = 2 2 ~ ω ω 2 /ω 2 n ω2 = 2 ~ α(0) r 1 n ω= ~ α(0) which leads to the Mavroyannis-Stephen (Slater-Kirkwood) approximation C6 ≈ J. Ángyán (EMQC) 3αA αB + (αB /nB )1/2 (αA /nA )1/2 IMF 174 / 201 Take another, equivalent form of the dynamic polarizability α(ω) = α+ (ω) + α+ (−ω) = 1 X |r on |2 1 X |r on |2 + 3~ ω0n + ω 3~ ω0n − ω n6=0 For ω = 0 α+ (ω) = n6=0 1 α(0) 2 For ω → ∞ ~ωα+ (ω) → 1X 1ˆ 1 |r 0n |2 = h0|r 2 |0i − h0|r|0i2 = (∆r)2 3 3 3 n6=0 Considering a one-term approximation α+ (ω) = J. Ángyán (EMQC) a0 ~(ω + ω) IMF 0 175 / 201 Taking the limiting cases one obtains a0 = 1 α(0) 2 ω= 2 (∆r)2 3~ α and we get the Salem-Tang-Karplus approximation C6 = αA αB αA /(∆r A )2 + αB (∆r B )2 For dimers it is identical to the Alexander upper bound C6 ≤ J. Ángyán (EMQC) 3 1 S(−2)S(−1) = α(∆r B )2 4 2 IMF 176 / 201 Solutions of the H + H dispersion problem The multipolar interaction Hamiltonian for two H atoms lying on the z axis, separated by a distance R0 is V̂ = − 2[R0−3 ξ1 ξ2 cos θ1 cos θ2 + βξ1 ξ22 cos θ1 (3 cos2 θ2 − 1) + γξ12 ξ22 (3 cos2 θ1 − 1)(3 cos2 θ2 − 1) + . . . p √ with polar ξ1,2 = r1,2 , α = ( 6/2)R0−3 , β = ( (30)/4)R0−4 and √ coordinates γ = ( 70/8)R−5 . By direct summation over the excited states, Eisenchitz and London obtained for the dipolar dispersion energy E (2) = − 12 X „ R06 n,m 1− ∆E z 2 ∆E z 2 «„ 0n 0n «„0m 0m 1 1 − m12 2 − n12 − n2 1 m2 « It is difficult to make converge this expression, because of the discrete-continuum matrix elements. The best value is C6 = 6.47. J. Ángyán (EMQC) IMF 177 / 201 The difficulties of the sum-over-states solution can be avoided by solving directly for the first-order wave function using the Ansatz proposed by Slater and Kirkwood, ψ(r 1 , r 2 ) = ψ0 (r1 , r2 )[1 + φ(r 1 , r 2 )] with the ground state unperturbed wave function of the dimer, ψ0 (r1 , r2 ). two-particle correlation function, φ, satisfies the differential equation The 1 2 ∇ φ + (∇ ln ψ0 ) · ∇φ) − v = 0 2 where v can be one of the multipolar terms of the interaction Hamiltonian. Taking the correlation function in the form vR(ξ, ξ 0 ) φ= E0 leads to a differential equation for R(ξ, ξ 0 ). Slater and Kirkwood (1931) obtained an approximate solution, leading to C6 = 6.23. Pauling and Beach (1935) used special orbitals to construct the Hamiltonian matrix and obtained C6 = 6.49903, C8 = 124.399 and C10 = 1135.21. Recent exact solutions obtained by Choy (P.R.A. 62 (2000) 012506) using orthogonal polynomials, confirm these values. J. Ángyán (EMQC) IMF 178 / 201 Part VI Short-range forces and their origin J. Ángyán (EMQC) IMF 179 / 201 Short-range forces and their origin Penetration effects Overlap repulsion – failure of the polarization approximation of PT Damping effects J. Ángyán (EMQC) IMF 180 / 201 Penetration effects: potential in the overlap region Take a charge distribution %(r) = f (ω)σ(r) with a radial part, which vanishes only at r → ∞. The general expression of the potential is V (R) = «Z ∞ Z ∞ „ l l X X 4π r< ∗ drr2 l+1 σ(r) dωYlm (ω)Ylm (Ω) 2l + 1 r> 0 l=0 m=−l The radial integral should be divided in two parts Z R Z ∞ rl Rl I(R) = drr2 l+1 σ(r) + drr2 l+1 σ(r) R r 0 R J. Ángyán (EMQC) IMF 181 / 201 Potential in the overlap region For instance, take an exponential function (STO) σ(r) = rn e−ar Use the integration rules ∞ Z drrn e−ar = 0 Z n! an+1 ∞ R drrn e−ar = n n! X (aR)k −ar e an+1 k! k=0 The radial integral I(R) = » n+1−l n+2+l X (aR)k −ar – X (aR)k −ar 1 n! 2l+1 · 1 − e + R e an+1 Rl+1 k! k! k=0 k=0 The potential of a 1s function (l = 0, n = 0) α3 σ(r) = 3 e−2αr π » – 1 −2αR V(1s)2 (R) = 1 − (1 + αR)e R In general, the potential of a charge distribution can be separated to a multipolar and penetration component. J. Ángyán (EMQC) IMF 182 / 201 Exact multipolar part of the potential In quantum chemistry, molecular charge densities are usually developed on Gaussian basis functions X X %(r) = Zα δ(r − R) − Pµν χ∗µ (r)χν (r) µν For this case, the multipolar potential can be exactly evaluated. Let us consider the χν (r) functions as primitive Gaussian functions of the general form χ(r) = R(r)Ylm (θ, φ) J. Ángyán (EMQC) IMF 183 / 201 The electronic contribution to the charge density is the sum of two types of terms: One-center densities, both basis functions are on the same atomic center %µν (r) = Rµ (r)Rν (r)Ylµ mµ (ω)Ylν mν (ω) Apply the sum rule (Clebsch-Gordan series) X m̄µ mν m Ylµ mµ (ω)Ylν mν (ω) = Klµ lν l Ylm (ω) lm with |lµ − lν | < l < lµ + lν and − mµ + mν + m = 0 The one-center densities can be written as a finite series of multipolar potentials (maximal order is lµ + lν ) around the natural expansion centre. Two-center densities can be handled in an analogous way, by using the Gaussian addition theorem, which leads to the natural expansion centre, the “barycenter” Rµν = αµ Rµ + αν Rν αµ + αν The multipole expansion wrt to the barycenter is finite, with the highest rank of multipole of lµ + lν . J. Ángyán (EMQC) IMF 184 / 201 Beyond the polarization approximation The RSPT applied to intermolecular interaction is often called polarization approximation, since it neglects effects that are related to the antisymmetry of the total wave function. In the following we shall discuss the failure of the polarisation approximation and one of the possible methods to remedy this situation. J. Ángyán (EMQC) IMF 185 / 201 H atom + proton system Zeroth order Hamiltonian and wave function and the perturbation potential are 1 1 H0 = − ∆ − 2 rA ϕ0 = 1sA V̂ = − 1 1 + rB R At R ≤ 0.05 a.u. (limit of united atoms) RSPT yields Eel (R) = −2 + 8 2 16 3 R + R + O(R4 ) 3 3 For very large intermolecular distances, R > 12 a.u., the total energy can be approximated as 2.25 1 7.5 E(R) = Eel + = − 4 − 6 + O(R−7 ) R R R J. Ángyán (EMQC) IMF 186 / 201 Convergence of the polarization approximation for H+ 2 0 ∆(n) = 100 @1 − n 1 2 3 4 5 6 8 12 16 20 30 38 1 Pn (k) k=1 ∆E A ∆Eexact R = 3.0 ∆E n ∆(n) 3.3050(-03) 10.26 -2.5686(-02) 71.14 -1.1074(-02) 56.87 -9.8501(-03) 44.17 -8.0099(-03) 33.84 -6.7955(-03) 25.08 -4.5279(-03) 12.03 -1.3808(-03) -0.41 +2.3496(-05) -2.40 +3.0523(-05) -1.07 -3.6059(-05) 0.30 -1.3906(-05) -0.07 R = 12.5 ∆E n ∆(n) 1.5000(-11) 100.000 -9.4250(-05) 27.809 -1.2599(-06) 26.844 -1.5711(-07) 26.723 -1.5409(-08) 26.711 -3.8934(-09) 26.708 -1.5287(-09) 26.706 -1.3304(-09) 26.702 -1.3244(-09) 26.698 -1.3241(-09) 26.694 -1.3241(-09) 26.683 -1.3241(-09) 26.675 Chalasinski et al. ĲQC 11 (1977) 247 At large R the exact wave function (with intermediate normalization) is ψ = ϕA + ϕB ≈ 1sA + 1sB i.e. the modification brought by the perturbation V̂ is not small at all. J. Ángyán (EMQC) IMF 187 / 201 ϕ0 ψ − ϕ0 −1/rA -10 -5 −1/rB 0 5 10 R (a.u.) near A V̂ is small, therefore ϕ0 = 1sA is good approximation near B V̂ is big, therefore ϕ0 = 1sA is very bad approximation. Expand the ψB = 1sB function by the eigenfunctions of A-centered basis X ψB = hψB |ak iak k At larger R bad convergence, since {ak } vanish exponentially at B. ∆E = J. Ángyán (EMQC) hϕ0 |V̂ ϕA i rapid convergence + IMF hϕ0 |V̂ ϕA i obtained only at inf. order 188 / 201 Example of two H atoms Interaction of two H atoms V̂ = − 1 1 1 − + r1B r2A r12 Unperturbed wave function ϕ0 = a0 (1)b0 (2) The RSPT charge density is a simple superposition of the 1s densities, %(r) = %1s (r − x) + %1s (r + x) In case of overlapping electron densities the antisymmetrized (triplet) wave function is 1 ψ0 = p [a0 (1)b0 (2) − a0 (2)b0 (1)] 2(1 − S 2 ) and the symmetry-adapted charge density is %(r) = J. Ángyán (EMQC) 1 [%1s (r − x) + %1s (r + x) − 2S1s(r − x)1s(r + x)] 1 − S2 IMF 189 / 201 Density depleted between nuclei %(r = 0) = ˜ 2 1 ˆ 2%1s (x) − 2S%1s (x) = %1s (x) < 2%1s (x) 1 − S2 1+S enhanced outside the nuclei, e.g. at r = 2x %(2x) ≈ ˜ 1 ˆ 1 %1s (x) + %1s (3x) ≈ %1s (x) > %1s (x) 1 − S2 1 − S2 The Hellmann-Feynmann forces will be repulsive. electron tunnels in both directions ⇒ exchange tunneling due to r112 the electronic motions become correlated ⇒ dispersion In many-electron systems the RSPT ground state violates Pauli-principle ⇒ antisymmetrized product would be a better ψ0 , but it is not eigenfunction of Ĥ0 . J. Ángyán (EMQC) IMF 190 / 201 U(R) Behaviour of the RSPT interaction energy ∆E(R) ∆EnRS (R) At short distances RSPT (polarization approximation) misses the repulsion: no acceptable minimum (RS) At large distance ∆E(R) − ∆En (R) vanishes exponentially, therefore the polarization approximation is acceptable. J. Ángyán (EMQC) IMF 191 / 201 Symmetry failure Why is the polarization approximation wrong at short and intermediate distances? Antisymmetrizer commutes with total Hamiltonian h i Â, (Ĥ + λV̂ ) = 0 but neither with Ĥ0 , nor with V̂ [Â, Ĥ0 ] 6= 0 [Â, V̂ ] 6= 0 It follows from the commutation rules that [Â, Ĥ0 ] = −λ[Â, V̂ ] i.e. non-zero zeroth-order and non-zero first order quantities are equal to each other: no unambiguous definition of the perturbation order. J. Ángyán (EMQC) IMF 192 / 201 Symmetry failure Antisymmetrized product states of the subsystems B ÂϕA a ϕb form a non-orthogonal set. A hermitian operator has always a orthogonal eigenfunctions. There can be no Hermitian Hamiltonian associated with these zeroth-order wave functions. Symmetry dilemma: Zeroth order Hamiltonian Ĥ(λ = 0) = ĤA + ĤB has lower symmetry than Ĥ(λ = 1)! N ĤA + ĤB SNA SNB Ĥ SNA +NB The direct product the symmetric groups of rank NA and NB is a subgroup of SNA +NB . Consequence: the polarization approximation is only asymptotically convergent, i.e. at a given intermolecular distance and orientation one cannot obtain the exact energy as a power series of the λ perturbational parameter. In the practice, PA is divergent at higher than 2nd order. J. Ángyán (EMQC) IMF 193 / 201 Claverie’s analysis The lowest eigenfunction of Ĥ(λ = 0) is a “bosonic” state, which is connected with the physically forbidden mathematical ground state of Ĥ(λ = 1), while the physical ground state of Ĥ(λ = 1) is connected with an excited state of Ĥ(λ = 0). Difference of p.g.s. and m.g.s. decreases exponentially with R. Since the m.g.s. becomes repulsive only at chemical bond distances, polarization approximation misses the repulsive effects. Two possible strategies: abandon the usual partition and find a Ĥ0 for which Âϕ0 is eigenfunction maintain the partition, but reject RSPT J. Ángyán (EMQC) IMF 194 / 201 Symmetrized RS perturbation theory Let the (NA + NB )-electron antisymmetrizer 1 Â = p (NA + NB )! X (−1)P P P ∈SN +N A B and set the following zeroth order approximation to the wave function, satisfying the intermediate normalization N0 = hϕ0 |Âϕ0 i−1 ψ0 = N0 Âϕ0 First iteration in the energy ∆E1 = N0 hϕ0 |V̂ Âϕ0 i First iteration in the wave function ψ1SRS = ϕ0 + N0 R̂0 (∆E1 − V̂ )Âϕ0 which is to be compared with the RSPT (polarization approximation, PA) result ψ1P A = ϕ0 − R̂0 V̂ ϕ0 where the second term vanishes as R → ∞. J. Ángyán (EMQC) IMF 195 / 201 Separation of the V̂ -dependent component of the first wave function iteration [Ĥ0 + V̂ , Â] = 0 −V̂ Â = Ĥ0 Â − Â(Ĥ0 + V̂ ) (∆E1 − V̂ )Â = Â∆E1 + Ĥ0 Â − ÂĤ0 − ÂV̂ (∆E1 − V̂ )Â = Â(∆E1 − V̂ ) + [Ĥ0 − E0 , Â] R̂0 [Ĥ0 − E0 , Â]ϕ0 = Âϕ0 − hϕ0 |Âϕ0 iϕ0 N0 R̂0 (∆E1 − V̂ )Âϕ0 = N0 Âϕ0 − N0 hϕ0 |Âϕ0 iϕ0 + N0 R̂0 Â(∆E1 − V̂ )ϕ0 = N0 Âϕ0 − ϕ0 + ψ (1) J. Ángyán (EMQC) IMF 196 / 201 The first iteration of the wave function can be decomposed as (exch) ψ1 = ϕ0 + ψ0 + ψ (1) i.e. a large exchange correction (exch) ψ0 = N0 Âϕ0 − ϕ0 and a small V̂ -dependent correction, ψ (1) = N0 R̂0 Â(∆E1 − V̂ )ϕ0 The second energy iteration gives ∆E2 = hϕ0 |V̂ ψ1 i = E (1) + E (2) with E (2) = N0 hϕ0 |V̂ R̂0 Â(∆E1 − V̂ )ϕ0 i and due to the hermiticity of V̂ and Â (1) E (2) = N0 hϕpol |Â(V̂ − ∆E1 )ϕ0 i J. Ángyán (EMQC) IMF 197 / 201 Separation of exchange contributions At any order of the SRS perturbation theory, the energy correction can be rigorously decomposed as a sum of exponentially decaying exchange component and the polarization component (n) (n) E (n) = Epol + Eexch This can be done using the decomposition of the total antisymmetrizer as Â = NA !NB ! ÂA ÂB (1 + P) (NA + NB )! where P is the sum of inter-system permutations. First order exchange energy (1) Eexch = hϕ0 |V̂ Pϕ0 i − hϕ0 |V̂ ϕ0 ihϕ0 |Pϕ0 i 1 + hϕ0 |Pϕ0 i Second order exchange energy (1) (2) Eexch = J. Ángyán (EMQC) (1) hϕpol |V̂ Pϕ0 i − hϕpol |V̂ ϕ0 ihϕ0 |Pϕ0 i 1 + hϕ0 |Pϕ0 i IMF 198 / 201 Symmetry adapted perturbation theory (SAPT) (Jeziorski, Moszynski, Szalewicz and Williams) Zeroth-order wave Hamiltonian is the sum of isolated molecule Fock operators and the solutions are expanded in a triple perturbation series Ĥ = F̂ A + F̂ B + ζ V̂ + λA ŴA + λB ŴB Consecutive application of the RSPT (polarization approximation) and symmetry adapted perturbation theory (exchange corrections) leads to the following expression of the interaction energy: ∞ ∞ X X (n) (n) ∆E = ∆Epol + ∆Eexch n=0 n=0 and both components are developed in the orders of the intramolecular correlation operator ∞ ∞ X ∞ ∞ X X X (nij) (n) (nij) (n) ∆Epol = ∆Epol ∆Eexch = ∆Eexch i=0 j=0 J. Ángyán (EMQC) i=0 j=0 IMF 199 / 201 SAPT Symbol (10) E pol (1n) E pol E (10) exch E (1n) exch Symbol Name Description Electrostatic Classical electrostatic interaction of unperturbed Hartree-Fock charge distributions Correlation correction to the electrostatic energy from the nth order intramolecular correlation effects on the charge distributions Electrostatic: correlation corrections Exchange (overlap) repulsion Repulsion of the closed shells: modification of the interaction energy of Hartree-Fock monomers due to the intermolecular antisymmetrization Exchange (overlap) repulsion: correlation corrections Intramolecular correlation correction to closed-shell repulsion Name (20) E ind (20) ind-exch (20) E disp E (20) E disp-exch (2n) E ind (2n) E disp Description Induction energy Energy arising from the distortion of each molecule in the field of the unperturbed Hartree-Fock charge distribution of the other Exchange induction Modification to the induction energy due to antisymmetry effects Dispersion energy Energy arising from the correlated fluctuations of the of the unperturbed Hartree-Fock charge distribution of each molecule Exchange dispersion Modification to the dispersion energy due to antisymmetry effects Induction energy: correlation corrections Corrections to the induction energy due to intramolecular correlation effects Dispersion energy: correlation corrections Corrections to the dispersion energy due to intramolecular correlation effects J. Ángyán (EMQC) IMF 200 / 201 SAPT decomposition of the He2 interaction energy (After: Korona et al. J. Chem. Phys. 106 (1997), 5109) J. Ángyán (EMQC) IMF 201 / 201

Top subcategories

Top subcategories

Top subcategories

Top subcategories

Top subcategories

Top subcategories

Top subcategories

Top subcategories

Download Intermolecular interactions