* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 6.6 General Form of the Equation for a Linear
System of polynomial equations wikipedia , lookup
Bra–ket notation wikipedia , lookup
Basis (linear algebra) wikipedia , lookup
Eigenvalues and eigenvectors wikipedia , lookup
Quartic function wikipedia , lookup
Cubic function wikipedia , lookup
Quadratic equation wikipedia , lookup
History of algebra wikipedia , lookup
Elementary algebra wikipedia , lookup
Linear algebra wikipedia , lookup
System of linear equations wikipedia , lookup
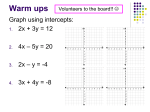
Linear Functions 6.6 : General Form of the Equation for a Linear Relation Today’s Objectives • Relate linear relations expressed in: slopeintercept form, general form, and slope-point form to their graphs, including: • Express a linear relation in different forms, and compare graphs • Rewrite a linear relation in either slope-intercept or general form • Graph, with or without technology, a linear relation in slope-intercept, general, or slope-point form • Identify equivalent linear relations from a set of linear relations • Match a set of linear relations to their graphs Equations of a Linear Function • We can make an equation that describes a line’s location on a graph. This is called a linear equation. There are three forms of linear equation that we will be looking at: • Standard Form: Ax + By + C = 0, where A, B, and C are integers. • Slope y-intercept form: y = mx + b, where m is the slope, and b is the y-intercept. • Slope-point form: y – y1 = m(x – x1), where m is the slope, and the line passes through a point located at (x1, y1) General form (or standard form) • Another form for the equation of a linear function is general form, or standard form: • 𝑨𝒙 + 𝑩𝒚 + 𝑪 = 𝟎 • In certain situations you will be asked to change the equation from slope y-intercept form into general form, and vice versa. • When converting the equation into standard form, we must remember that A, B, and C, MUST be integers, which means all fractions need to be removed. We also need to remember to move all terms to the same side of the equation to make it equal to zero. Example Write the following in general form: y – 1 = 2/3(x + 2) Multiply both sides by 3: 3(y – 1) = 2(x+2) Expand: 3y – 3 = 2x + 4 Make equation = 0 Collect Like Terms Arrange in proper order 3y – 2x – 7 = 0 -2x + 3y – 7 = 0 Example Write the following in general form: y + 2 = 3/5(x - 4) Multiply both sides by 5 5y + 10 = 3(x – 4) Remove the brackets 5y + 10 = 3x – 12 Collect all terms on one side of the equation 5y = 3x – 12 – 10 0 = 3x – 5y - 22 What does the graph look like? A=0 Ax + By + C = 0 By + C = 0 y = -C/B Since –C/B is a constant, the graph will be a horizontal line B=0 Ax + By + C = 0 Ax + C = 0 x = -C/A Since –C/A is a constant, the graph will be a vertical line Example Graph the line 2x – 5y – 10 = 0 Determine the x-intercept Let y=0 and solve for x 2x – 5(0) – 10 = 0 2x – 10 = 0 2x = 10 x=5 (5,0) Determine the y-intercept Let x=0 and solve for y 2(0) – 5y – 10 = 0 -5y – 10 = 0 -5y = 10 y = -2 (0,-2) Plot the points and draw a line through them. Example Determine the slope of 2x – 5y – 10 = 0 Rewrite the equation in slope-interval form: 2x – 5y – 10 = 0 -5y = -2x + 10 y = -2x + 10 -5 y = -2x/-5 + 10/-5 y = 2/5x – 2 m = 2/5 solve for y Example Determine the slope of -3x – 2y – 16 = 0 Rewrite the equation in slope-interval form: -3x – 2y – 16 = 0 -2y = 3x + 16 y = 3x + 16 -2 y = 3x/-2 + 16/-2 y = -3/2x – 8 m = -3/2 solve for y