Download Proving that Figures are Special Quadrilaterals.

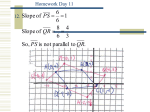
By,
Michael Thiel and Lauren Larar.
 First,
you must identify what family the quadrilateral
falls under.
Parallelogram,
Trapezoid ,
quadrilateral.
 1.
If a parallelogram contains at least one
right angle, then it is a rectangle.
 2. I the diagonals of a parallelogram are
congruent, then the parallelogram is a
rectangle.
*You can also prove that a quadrilateral is
rectangle without first showing that it is a
parallelogram.*
 1. If all four angles of a quadrilateral are
right angles, then it is a rectangle.
 1.
If two disjoint pairs of consecutive sides of
a quadrilateral are congruent, then it is a
kite.
 2.
If one of the diagonals of a quadrilateral is
the perpendicular bisector of the other
diagonal, then the quadrilateral is a kite.
 1.
If a parallelogram contains a pair of
consecutive sides that are congruent, then it
is a rhombus.
 2. If either diagonal of a parallelogram
bisects two angles of the parallelogram, then
it is a rhombus.
*You can also prove that a quadrilateral is a
rhombus without first showing that it is a
parallelogram.*
 1.If the diagonals of a quadrilateral are
perpendicular bisectors of each other, then
the quadrilateral is a rhombus.
1.
If a quadrilateral is both a
rectangle and a rhombus, then it
is a square.
 1.If
the nonparallel sides of a trapezoid are
congruent, then it is isosceles.
 2. If the lower or the upper base angles of a
trapezoid are congruent, then it is isosceles.
 3. If the diagonals of a trapezoid are
congruent, then it is isosceles.
2 column proof sample problem!
S
1.) ME
R
1.) Given
 MI
2.) Given
2.) KM bisects <EMI
3.) <EMT
4.) MT

5.)
EMT
6.) <ETM
3.) If a seg bisecvts the <, it divides the < into 2
congruent segs.
 < IMT
MT


4.) Reflexive
IMT
5.) SAS (1,3,4)
<ITM
6.) CPCTC
7.) CPCTC
7.) ET  TI
8.) If two adjacent angles form a straight angle, they are
suppl.
9.) If 2 angles are both suppl and cong., they are rt angles
10.) If 2 pts are =dist from the segs endpts, it det. The perp
bis of a seg.
8.)<ETM suppl. <TIM
9.) <ETM, <ITN rt <s
10.) KM perp. bis. EI
11.)MIKE is a kite
11.) If one of the diags of a quad is the perp bis of the other
diag, then the quad is a kite.
M
E
T
K
I
1.
--->
Rhombus!
2.
----->
Isosceles Trapezoid
Practice Problems!
1.
1. Given
2
.
2. Perpendicular lines meet to form right angles
3.
4.
parallel.
4. In a plane, lines perpendicular to the same line
are parallel.
5.
5. A quadrilateral with two sets of opposite
6.
3. The opposite sides of a parallelogram are
parallel sides is a parallelogram.
6. A parallelogram with one right angle is a
rectangle
 In
order for MIKE to be a rectangle, what
must the value of X be?
M
E
I
2x+40+30=90
2x+70=90
2x=20
X=10
2(10)+40+30=90
K
In order to prove this quadrilateral to be a rectangle, one
side must be right.
A right angle is 90 degrees, therefore, the measurements
of each angle must be added together and set equal to 90
degrees. Then the value of X must be found. In order for
this quadrilateral to be a rectangle, the value of X must be
20.
 Find
the area of the parallelogram
(10,8)
(-2,6)
(-2,0)
(10,2)
In order to find the
area of the
parallelogram, first,
the length of the sides
must be determined. In
addition, the opposite
sides are congruent
due to the fact that it
is a parallelogram.
Therefore, after
finding one side to be 6
and the other side to
be 8, multiply the
length by width. (6x8=
48) The area is 48.
A Greek mathematician
became interested in the
Golden Ratio, a ratio of
about 1:1.618. A rectangle
whose side lengths are in
the golden ratio is called a
Golden Rectangle. These
rectangles are believed to
be especially pleasing to
look at. The Golden Ratio
has been found in many
works of art and
architecture such as the
Parthenon at the left.
"Coordinate Geometry Proofs." Oswego City School District Regents Exam Prep
Center. Web. 19 Jan. 2011.
<http://www.regentsprep.org/regents/math/geometry/GCG4/CoordinatepRA
CTICE.htm>.
McDougal Littell Geometry Applying, Reasoning, Measuring. Evanston, IL:
McDougal Littell, 2005. Print.
"Practice with Quadrilaterals." Oswego City School District Regents Exam Prep
Center. Web. 19 Jan.2011.
<http://www.regentsprep.org/Regents/math/geometry/GP9/PracQuadPf.htm
>.
Rhoad, Richard, George Milauskas, and Robert Whipple. Geometry for Enjoyment
and Challenge. Evanston, IL: McDougal, Littell, 1991. Print