Download Bayesian Decision Theory

Bayesian Decision Theory
Compiled By:
Raj Gaurang Tiwari
Assistant Professor
SRMGPC, Lucknow
Statistical Pattern Recognition
 The design of a recognition system requires careful attention
to the following issues:
 definition of pattern classes,
 sensing environment
 pattern representation
 feature extraction and selection
 cluster analysis
 classifier design and learning
 selection of training and test samples
 performance evaluation.
Statistical Pattern Recognition…..
 In statistical pattern recognition, a pattern is represented by a
set of d features, or attributes, viewed as a d-dimensional
feature vector.
 Well-known concepts from statistical decision theory are
utilized to establish decision boundaries between pattern
classes.
 The recognition system is operated in two modes: training
(learning) and classification (testing)
Model for statistical pattern recognition
 The role of the preprocessing module is to segment the pattern of
interest from the background, remove noise, normalize the
pattern, and any other operation which will contribute in defining
a compact representation of the pattern.
 In the training mode, the feature extraction/selection module
finds the appropriate features for representing the input patterns
and the classifier is trained to partition the feature space. The
feedback path allows a designer to optimize the preprocessing and
feature extraction/selection strategies.
 In the classification mode, the trained classifier assigns the input
pattern to one of the pattern classes under consideration based on
the measured features.
Decision theory
 Decision theory is the study of making decisions
that have a significant impact
 Decision-making is distinguished into:
 Decision-making under certainty
 Decision-making under non-certainty
 Decision-making under risk
 Decision-making under uncertainty
Probability theory
 Most decisions have to be taken in the presence of
uncertainty
 Probability theory quantifies uncertainty regarding the
occurrence of events or states of the world
 Basic elements of probability theory:
 Random variables describe aspects of the world whose
state is initially unknown
 Each random variable has a domain of values that it can
take on (discrete, boolean, continuous)
 An atomic event is a complete specification of the state
of the world, i.e. an assignment of values to variables
of which the world is composed
Probability Theory..
 Probability space
 The sample space S={e1 ,e2 ,…,en } which is a set of
atomic events
 Probability measure P which assigns a real number
between 0 and 1 to the members of the sample space
 Axioms
 All probabilities are between 0 and 1
 The sum of probabilities for the atomic events of a
probability space must sum up to 1
 The certain event S (the sample space itself) has
probability 1,and the impossible event which never
occurs, probability 0
Prior
 Priori Probabilities or Prior reflects our prior
knowledge of how likely an event occurs.
 In the absence of any other information, a
random variable is assigned a degree of belief
called unconditional or prior probability
Class Conditional probability
 When we have information concerning previously
unknown random variables then we use posterior
or conditional probabilities: P(a|b) the
probability of a given event a that we know b
P ( a  b)
P ( a | b) 
P(b)
 Alternatively this can be written (the product
rule):
P(a  b)=P(a|b)P(b)
Bayes’ rule
 The product rule can be written as:
 P(a  b)=P(a|b)P(b)
 P(a  b)=P(b|a)P(a)
 By equating the right-hand sides:
P(a | b) P(b)
P(b | a) 
P(a)
 This is known as Bayes’ rule
Bayesian Decision Theory
 Bayesian Decision Theory is a fundamental statistical
approach that quantifies the tradeoffs between various
decisions using probabilities and costs that accompany
such decisions.
 Example: Patient has trouble breathing
– Decision: Asthma versus Lung cancer
– Decide lung cancer when person has asthma
 Cost: moderately high (e.g., order unnecessary tests, scare
patient)
– Decide asthma when person has lung cancer
 Cost: very high (e.g., lose opportunity to treat cancer at early
stage, death)
Decision Rules
 Progression of decision rules:
 – (1) Decide based on prior probabilities
 – (2) Decide based on posterior probabilities
 – (3) Decide based on risk
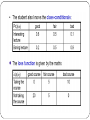
Fish Sorting Example Revisited
Decision based on prior probabilities
Question
 Consider a two-class problem, { c1 and c2 } where the prior
probabilities of the two classes are given by
 P ( c1 ) = ⋅7 and P ( c2 ) = ⋅3
 Design a classification rule for a pattern based only on prior
probabilities
 Calculation of Error Probability – P ( error )
Solution
Decision based on class conditional
probabilities
Posterior Probabilities
Bayes Formula
 Suppose the priors P(wj) and conditional densities p(x|wj)
are known,
prior
likelihood
P( j | x) 
posterior
p( x |  j ) P( j )
p ( x)
evidence
Making a Decision
Probability of Error
Average probability of error
P(error)
Bayes decision rule minimizes this error because
 The dotted line at x0 is a threshold partitioning the feature
 space into two regions,R1 and R2. According to the Bayes
decision rule,for all values
 of x in R1 the classifier decides 1 and for all values in R2 it decides
2. However,
 it is obvious from the figure that decision errors are
unavoidable.
Example of the two regions R1 and R2 formed by the Bayesian
classifier for the case of two equiprobable classes.
The dotted line at x0 is a threshold partitioning the feature space into two
regions,R1 and R2. According to the Bayes decision rule, for all values of x in
R1 the classifier decides 1 and for all values in R2 it decides 2. However, it is
obvious from the figure that decision errors are unavoidable.
total probability,Pe,of committing a
decision error
 which is equal to the total shaded area under the curves in
Figure
Minimizing the Classification Error
Probability
 Show that the Bayesian classifier is optimal with respect to
minimizing the classification error probability.
Generalized Bayesian Decision Theory
Bayesian Decision Theory…
Bayesian Decision Theory…
Conditional Risk
Minimum-Risk Classification
•For every x the decision function α(x) assumes one of the a
values α1, ..., αa.
The overall risk R is the expected loss associated with a given
decision rule.
Two-category classification
1 : deciding 1
2 : deciding 2
ij = (i | j)
loss incurred for deciding i when the true state of nature is j
Conditional risk:
R(1 | x) = 11P(1 | x) + 12P(2 | x)
R(2 | x) = 21P(1 | x) + 22P(2 | x)
Our rule is the following:
if R(1 | x) < R(2 | x)
action 1: “decide 1” is taken
This results in the equivalent rule :
decide 1 if:
By employingBayes’ formula
(21- 11) P(x | 1) P(1) > (12- 22) P(x | 2) P(2)
and decide 2 otherwise
Likelihood ratio
P( x | 1 ) 12  22 P(2 )
if

.
P( x | 2 ) 21  11 P(1 )
Then take action 1 (decide 1)
Otherwise take action 2 (decide 2)
Example
 Suppose selection of w1 and w2 has same probability:
P(w1)=p(w2)=1/2
Assume that the loss matrix is of the form
 If misclassification of patterns that come from w2 is
considered to have serious consequences, then we must
choose 12 > 21.
 Thus, patterns are assigned to w2 class if
21
P( x | 2 ) 
P( x | 1 )
12
 That is, P(x | 1) is multiplied by a factor less than 1
Example
Minimum-Error-Rate Classification
 The action αi is usually interpreted as the decision that the
true state of nature is ωi.
 Actions are decisions on classes
If action i is taken and the true state of nature is j then:
the decision is correct if i = j and in error if i  j
 Seek a decision rule that minimizes the probability of error which is the
error rate
 Introduction of the zero-one loss function:
0 i  j
 ( i ,  j )  
1 i  j
i, j  1,..., c
Therefore, the conditional risk is:
j c
R( i | x)    ( i |  j ) P( j | x)
j 1
  P( j | x)  1  P(i | x)
j i
“The risk corresponding to this loss function is the average
probability error”
 Minimizing the risk requires maximizing P(i | x)
(since R(i | x) = 1 – P(i | x))
 For Minimum error rate
 Decide i if P (i | x) > P(j | x) j  i