Download : Sparse Matrix Algorithms CS 290N / 219 )

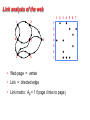
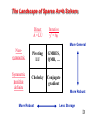
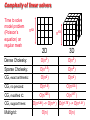
CS 290N / 219: Sparse Matrix Algorithms
John R. Gilbert ([email protected])
www.cs.ucsb.edu/~gilbert/cs290
Systems of linear equations:
Ax = b
Systems of linear equations: Ax = b
• Alice is four years older than Bob.
• In three years, Alice will be twice Bob’s age.
• How old are Alice and Bob now?
Link analysis of the web
1
1
2
2
3
4
1
2
3
4
7
5
4
5
6
3
6
7
• Web page = vertex
• Link = directed edge
• Link matrix: Aij = 1 if page i links to page j
5
6
7
Web graph: PageRank (Google)
[Brin, Page]
An important page is one that
many important pages point to.
• Markov process: follow a random link most of the time;
otherwise, go to any page at random.
• Importance = stationary distribution of Markov process.
• Transition matrix is p*A + (1-p)*ones(size(A)),
scaled so each column sums to 1.
• Importance of page i is the i-th entry in the principal
eigenvector of the transition matrix.
• But, the matrix is 10,000,000,000 by 10,000,000,000.
Mark Adams: Bone Density Modeling
Poisson’s equation for temperature
The (2-dimensional) model problem
n1/2
• Graph is a regular square grid with n = k^2 vertices.
• Corresponds to matrix for regular 2D finite difference mesh.
• Gives good intuition for behavior of sparse matrix
algorithms on many 2-dimensional physical problems.
• There’s also a 3-dimensional model problem.
Solving Poisson’s equation for temperature
k = n1/3
• For each i from 1 to n, except on the boundaries:
– x(i-k2) – x(i-k) – x(i-1) + 6*x(i) – x(i+1) – x(i+k) – x(i+k2) = 0
• n equations in n unknowns: A*x = b
• Each row of A has at most 7 nonzeros.
Graphs and Sparse Matrices: Cholesky factorization
Fill: new nonzeros in factor
3
1
6
8
4
9
7
G(A)
2
4
9
7
6
8
10
5
3
1
10
5
G+(A)
[chordal]
2
Symmetric Gaussian elimination:
for j = 1 to n
add edges between j’s
higher-numbered neighbors
The Landscape of Sparse Ax=b Solvers
Direct
A = LU
Iterative
y’ = Ay
More General
Nonsymmetric
Symmetric
positive
definite
Pivoting
LU
GMRES,
QMR, …
Cholesky
Conjugate
gradient
More Robust
More Robust
Less Storage
D
Complexity of linear solvers
Time to solve
model problem
(Poisson’s
equation) on
regular mesh
n1/2
n1/3
2D
3D
Dense Cholesky:
O(n3 )
O(n3 )
Sparse Cholesky:
O(n1.5 )
O(n2 )
CG, exact arithmetic:
O(n2 )
O(n2 )
CG, no precond:
O(n1.5 )
O(n1.33 )
CG, modified IC:
O(n1.25 )
O(n1.17 )
CG, support trees:
Multigrid:
O(n1.20 ) -> O(n1+ ) O(n1.75 ) -> O(n1.31 )
O(n)
O(n)
Administrivia
• Course web site: www.cs.ucsb.edu/~gilbert/cs290
• Join the email (Google) discussion group!! (see web site)
• First homework is on the web site, due next Monday
• About 5 weekly homeworks, then a final project
(implementation experiment, application, or survey paper)
• Assigned readings: Davis book, Saad book (online), MGT.
(Library reserve; see me for an extra copy of Davis.)