Download Improvement of Gilbert Cell`s Dynamic Range by Predistortion of

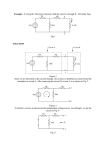
International Symposium for Design and Technology of Electronic Packages - 11th Edition, Cluj-Napoca, Romania
Improvement of Gilbert Cell’s Dynamic Range by
Predistortion of Input Signals
Radu Gabriel BOZOMITU, Daniela Ionescu, Vlad Cehan
Department of Telecommunications, Faculty of Electronics and Telecommunications,
“Gh. Asachi” Technical University, Carol I No.11 Av., 700506, Iaúi, Romania, Phone: +40-232-213737
[email protected] [email protected] [email protected]
Abstract
One of the most severe limitations of Gilbert cell, implemented in bipolar technology, is that this
circuit does not allow input signals with a magnitude higher than VT (thermal voltage), operating
in the following as analog multiplier. For many radiofrequency applications which require the
analog multiplier function, the large signals operation is still very important.
In this paper, the possibilities of increasing the input signal dynamic range of Gilbert cell, so
that it preserves its role of analog multiplier, is analyzed.
The technique of increasing dynamic range of Gilbert multiplier, analyzed in this paper, consists
in predistortion of its input signals by using an inverse transfer function of “arctanh” type. So, by
compensation of both nonidealities (the input one – “arctanh” type deliberately introduced and
the “tanh” type – realized by the simple Gilbert cell) a significant increase of the dynamic range
for which the circuit realizes the analog multiplier function, without distorting the input signals, is
obtained.
In the paper, an original technique for the predistortion of the input signals is presented and the
complete electric schematic of the proposed circuit in a 0.8 μm BiCMOS technology is shown.
The simulations performed in considered technology confirms the theoretically obtained results.
1. INTRODUCTION
Ic3-5
For the analog signals processing a circuit which
allows for inputs two analog signals and produces an
output signal proportional with their product, is often
necessary. Such circuits are termed analog multipliers
[1] – [3].
Gilbert cell analog multiplier operating is based
on the exponential transfer function of bipolar
transistors.
Multiplying Gilbert cell, analyzed in this paper, is
in fact, a modification of the emitter coupling cell
which allows to obtain a four-quadrant operating. This
cell is the base element for most of the integrated
systems which realize a balanced multiplication [1].
Serial connecting of an emitter coupling pair with
other same pairs cross connected produces an
extremely useful transfer characteristic, which will be
analyzed in the following sections.
Input signals magnitude is often much higher than
thermal voltage (VT = 26 mV) in many applications.
The possibility of operating also in these terms of
the Gilbert cell as analog multiplier is analyzed in this
paper.
Ic3
Q3
+
Q5
Ic6
Q6
Ic1
V1
-
Ic4-6
Ic5
Ic4
Q4
+
Ic2
Q1
Q2
V2
-
I0
I0
Fig. 1. Electrical schematic of a Gilbert cell analog
multiplier
The differential output current is expressed as [1]:
§ V ·
§ V ·
' I I 0 tanh ¨ 1 ¸ tanh ¨ 2 ¸
(1)
© 2VT ¹
© 2VT ¹
So, the dc transfer characteristic is given by the
product between hyperbolic tangent of the two input
voltages.
2. GILBERT CELL AS ANALOG MULTIPLIER
The electric schematic of the analog multiplier
made by Gilbert cell is shown in Fig. 1.
ISBN 973-713-063-4
ǻI = Ic4-6 - Ic3-5
41
International Symposium for Design and Technology of Electronic Packages - 11th Edition, Cluj-Napoca, Romania
Practical applications of the multiplier cell can be
divided into three categories according to the
magnitude relative to VT of applied signals V1 and V2.
If the magnitudes of V1 and V2 signals are lower
than VT, then hyperbolic tangent function can be
approximated as linear and the circuit behaves as
multiplier, developing the product of V1 and V2. By
serial including with each input of a nonlinear circuit
(to compensate the hyperbolic tangent dependence),
the input voltages range over which linearity is
maintained can be greatly extended.
The second class of applications is characterized
by the fact that to one of the inputs is applied a large
signal, compared to VT; causing the transistor to which
that signal is applied to behave like switches rather
than near-linear devices. For this operating mode, the
applied small signal is effectively multiplied by a
square wave, and the circuit acts as a modulator.
In the third class of applications, the signals
applied to both inputs are large compared to VT; and
all six transistors in the circuit behave as nonsaturating
switches. This mode of operation is useful for the
detection of phase differences between two amplitudelimited signals, as is required, for example, in phaselocked loops. This operating mode is sometimes called
the phase-detector mode.
In this paper, a method to increase the dynamic
range of the Gilbert cell by input signals predistortion
using an „arctanh” function is presented. So, by
compensating the two nonlinearities (“arctanh” type –
applied to both inputs and that of “tanh” type –
realized by Gilbert circuit), the dynamic range for
which linearity is preserved (the circuit realizing the
analog multiplier function) can be greatly extended.
Unlike other linearization techniques shown in
literature (for which linear operating is obtained only
in a limited range around the dc transfer characteristic
origin [1]), the following proposed technique allows to
obtain a linear operating for the entire dynamic range
in which the input predistortion circuit transfer
characteristic can be considered as “arctanh” type.
3. GETTING OF THE INPUT
BY “ARCTANH” TYPE
–
Iout
OTA
V0
Iin
+
Ibias
Fig. 2. Getting the inverted transfer function by
negative feedback
The complete electric schematic of the input predistortion circuit (by “arctanh” type) can be followed
in Fig. 3.
Ec
Q3
Q4
Iin
V0
Q1
Q2
Ibias
Fig. 3. Electrical schematic of an „arctanh” type
predistortion circuit
For a „tanh” transconductor, the output current is
given by the following relation:
§ V ·
I out I bias tanh ¨ 0 ¸
(4)
© 2VT ¹
For „arctanh” predistortion circuit from Fig. 3, the
output predistortion voltage V0 can be expressed as:
§ I ·
V0 2VT arctanh ¨ in ¸
(5)
© I bias ¹
In Fig. 4 are shown the dc transfer characteristics
of the predistortion circuit by „arctanh” type for
different values of the bias current Ibias.
The dynamic range of the input current applied to
circuit from Fig. 3, results from the existence
conditions of „arctanh” function, as:
I bias I in I bias
(6)
PREDISTORTION CIRCUIT
By using a negative feedback for an operational
transconductance amplifier (OTA) by “tanh” type, as
Fig. 2 shows, the inverted transfer function is
obtained.
For the OTA in Fig. 2 we can write:
I out K ˜ f ( V0 ) ; I out I in
(2)
Because the „tanh” transconductors have odd
transfer characteristics ( f ( V0 ) f (V0 ) ), from
equations (2) we obtain:
I in K ˜ f (V0 ) ; V0 f 1 I in K (3)
0.10
DC.V0
0.05
0.00
-0.05
-0.10
500
400
300
200
100
0
-100
-200
-300
-400
-500
DC.Iin, μA
Fig. 4. Dc transfer characteristics of an „arctanh” type
predistortion circuit (Ibias = 100μA - 500μA)
ISBN 973-713-063-4
42
International Symposium for Design and Technology of Electronic Packages - 11th Edition, Cluj-Napoca, Romania
Another way to obtain a wider dynamic range for
the input voltages is to deliberately introduce a
nonlinearity which predistorts the input signals, so
compensating the transfer characteristic by “tanh”
type of the base cell. Thus the nonlinearity which must
be introduced is of “arctanh” form.
A hypothetic example for such a system is given
in [1], which use the emitter degeneration for the
lower emitter coupled pair. The disadvantage of the
system shown in [1] is that it allows obtaining a linear
operating only in a limited range around the dc
transfer characteristic origin.
The following proposed technique allows
obtaining a wider dynamic range, represented by the
entire range where the input predistortion transfer
characteristic can be considered as “arctanh” type.
The mean idea of this technique is to use
“arctanh” predistortion circuits (as that from Fig. 3) to
the inputs of Gilbert cell shown in Fig. 1. In this way
the electric schematic of the proposed circuit is obtain,
as Fig. 5 shows.
Thus the predistortion voltages of the modified
Gilbert cell's two inputs, shown in Fig. 5, according to
relation (5), can be expressed as:
§ I ·
(11)
V01 2VT arctanh ¨ in1 ¸
© I bias ¹
4. COMPENSATION OF THE GILBERT CELL NONLINEARITY BY INPUTS SIGNALS PREDISTORTION
The hyperbolic-tangent function allows the
following serial development:
x3
tanh( x ) x (7)
3
Assuming that x 1 , the „tanh” function may
be approximated as follows:
tanh( x ) | x
(8)
Applying this approximation in equation (1)
written as,
V1 , V2 2VT
(9)
we will obtain:
§ V ·§ V ·
' I | I0 ¨ 1 ¸ ¨ 2 ¸
(10)
© 2VT ¹ © 2VT ¹
Thus for small-amplitude signals, the circuit
performs as analog multiplier.
But, for many radio-frequency applications, the
input signals magnitude is much larger than VT. In the
following, the possibility that the circuit allows also
larger magnitude input signals, still operating as
analog multiplier, is analyzed. When only one of the
input signals is larger than VT, one can use the emitter
degeneration for the lower emitter coupled pair; thus
the V2 signal magnitude range is increased, still
allowing a linear operating. This technique cannot be
applied, however, to cross connected pairs Q3 – Q6
because the degeneration resistors presence impedes
the realization of the needed nonlinear relation
between Ic (collector current) and Vbe (base-emitter
voltage).
Q19
Q20
Iin1
§I ·
2VT arctanh ¨ in 2 ¸
(12)
© I bias ¹
By using equations (11) and (12) in relation (1),
we obtain:
I0
'I
(13)
I in1 I in 2
2
I bias
V02
Q7
Q8
Ic3-5
Q17
Ec
Q10
Q9
Ic4-6
Ic4-6
V01
Q18
Ic3
C1
Ibias
Ic5
Ic4
Q3
Q4
Q5
Ic6
Vout
Q6
ǻI = Ic4-6 - Ic3-5
Q15
Q16
Iin2
Ic1
Ic2
Ic3-5
C2
Q1
Q2
Q11
Q13
Q14
Q12
V02
I0I0
Ibias
Fig. 5. Electrical schematic of a Gilbert cell analog multiplier with “arctanh” type predistortion circuits
ISBN 973-713-063-4
43
International Symposium for Design and Technology of Electronic Packages - 11th Edition, Cluj-Napoca, Romania
Thus by compensating nonlinearities, according
to relation (13), one can obtain a current mode circuit,
which realizes the analog multiplier function and
which has a dynamic range superior to simple Gilbert
cell illustrated in Fig. 1.
To simplify the representation, in the electric
schematic of the proposed circuit from Fig. 5 were not
represented the bias resistors; the ac coupling between
the predistortion circuits and Gilbert cell's inputs were
considered.
the inputs signals for which the circuit realizes the
analog multiplier function.
TRAN.Out, V
1.0
0.0
-0.5
-1.0
180
5. SIMULATIONS RESULTS
185
190
195
200
time, usec
The output signal’s spectrum of an ideal double
balanced analog multiplier made by Gilbert cell is
formed only by two spectral lines with equal
magnitudes, one on the frequency sum ( f 01 f 02 )
and other on the frequency difference ( f 02 f 01 ) of
the two harmonic inputs signals applied. In order to
asses the distortion level of the output signal for such
an analog multiplier, one can calculate the total
harmonic distortion (THD) for the output signal,
considering the harmonic distortions reported to one
of the two main spectral lines.
In order to compare the two circuits performances
(from Fig. 1 and from Fig. 5), one should simulate in
identical conditions, applying voltage and current
input signals, respectively. In both situations one
should use the input signals having magnitudes chosen
so that to obtain maximal magnitude of ( f 01 f 02 )
and ( f 02 f 01 ) output harmonics, for which the
output signals harmonic distortion is THD d 5% for
both circuit. It is noticed that for the Gilbert cell with
predistortion circuits, the magnitude of ( f 01 f 02 )
and ( f 02 f 01 ) output harmonics obtained, for which
THD d 5% , is larger than for the analog multiplier
with unmodified standard Gilbert cell.
In the paper, another method to compare the two
circuits performances, is presented, too. Harmonic
signals are applied to both circuits inputs, so that the
magnitudes of the two main spectral lines to be
identical for both circuits. It is noticed that for the
Gilbert cell with predistortion circuits, the THD value
is smaller than for unmodified standard Gilbert cell.
The voltage supply for the proposed circuit shown
in Fig. 5 is EC = 3.3V, and the following presented
simulations were performed by considering a load
resistance RL = 20 kȍ.
For the input predistortion circuits from the
proposed circuit shown in Fig. 5 a bias current Ibias =
500μA was used; for Gilbert cell of the proposed
circuit a bias current I0 = 1mA was used.
The following simulations were made by
considering the analog multiplier operating of the
proposed circuit, when an output signal, proportional
with the product of the two inputs signals, is obtained.
We mentioned already that the operation as
analog multiplier of the standard Gilbert cell (Fig. 1)
has the disadvantage of a very small dynamic range of
ISBN 973-713-063-4
0.5
Fig. 6. Output voltage waveform
(Ibias = 500μA, I0 = 1mA)
10
TRAN.sd, mV
5
0
-5
-10
100
120
140
160
180
200
time, usec
Fig. 7. Waveform of a V01 input predistorted voltage
(f01 = 100 kHz, Ibias = 500μA, I0 = 1mA)
TRAN.pd, mV
100
50
0
-50
-100
190
192
194
196
198
200
time, usec
var("TRAN.I_Ic4-6.i"), uA
var("TRAN.I_Ic3-5.i"), uA
Fig. 8. Waveform of a V02 input predistorted voltage
(f02 = 1 MHz, Ibias = 500μA, I0 = 1mA)
600
550
500
450
400
180
185
190
195
time, usec
Fig. 9. Currents Ic3-5 and Ic4-6 waveforms
(Ibias = 500μA, I0 = 1mA)
44
200
mag(Tran1.VspecTran1)
International Symposium for Design and Technology of Electronic Packages - 11th Edition, Cluj-Napoca, Romania
case, the magnitudes of both inputs voltage signals,
for which the undistorted analog multiplier operating
is obtained (having THD d 5% ), are: Vin1max = 10
mV and Vin2max = 30 mV, respectively.
The simulations presented in Fig. 10 and 11
confirm that, for the Gilbert cell with predistortion
circuits, the magnitude of ( f 01 f 02 ) and ( f 02 f 01 )
output harmonics obtained, for which THD d 5% , is
significantly larger (0.3V, according to Fig. 10) than
for the analog multiplier with unmodified standard
Gilbert cell (0.17V, according to Fig. 11).
To verify the second method for comparing the
two circuit performances, the harmonic voltage and
current signals are applied to both circuits inputs,
respectively, having magnitudes chosen so that the
magnitudes of the two main spectral lines are identical
for both circuits (0.2V). From the simulations
performed for this situation, results that for the Gilbert
cell with predistortion circuits an output signal having
THD 4.5% is obtained and for unmodified
standard Gilbert cell an output signal with
THD 6% result.
From the simulations presented above one notice
that the output dynamic range of the proposed circuit
is significantly wider than that obtained for standard
Gilbert cell.
0.4
0.3
0.2
0.1
0.0
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
freq, MHz
mag(Tran1.VspecTran1)
Fig. 10. Output voltage magnitude spectrum of a
proposed circuit from Fig. 5
0.20
0.15
0.10
0.05
0.00
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
freq, MHz
Fig. 11. Magnitude spectrum of the output voltage
signal for a standard Gilbert cell, identical
to that used in the proposed circuit from
Fig. 5, but without predistortion circuits
6. CONCLUDING REMARKS
Using the proposed circuit from Fig. 5 we can
significantly increase the dynamic range for which the
circuit realizes the analog multiplier function.
For analyzing, to the inputs of the proposed
circuit shown in Fig. 5, two current signals are
applied: Iin1 (having the magnitude Iin1max = 80 μA
and frequency f01 = 100kHz) and Iin2 (having the
magnitude Iin2max = 450 μA and frequency f02 =
1MHz).
In Fig. 6 is shown the waveform of the output
voltage specific for analog multiplier operating of the
proposed circuit from Fig. 5.
In Fig. 7 and 8 the V01 and V02 predistortion
voltages of the Gilbert cell's inputs from Fig. 5 are
represented. One notices their significant deviation of
the harmonic form.
The waveforms of the Ic3-5 and Ic4-6 currents,
obtained at predistortion circuits Gilbert cell's outputs
are shown in Fig. 9.
In Fig. 10 the magnitude spectrum of the output
voltage signal for proposed circuit shown in Fig. 5 is
presented. This spectrum is obtained for maximal
values of the input signals magnitudes (illustrated
above) for which an undistorted output signal
( THD d 5% ), proportional to their product, is
obtained.
In Fig. 11 the magnitude spectrum of the output
voltage signal for standard Gilbert cell from Fig. 1,
identical to that used in the proposed circuit from Fig.
5, but without predistortion circuits, is shown. This
spectrum was obtained in the same conditions as those
described above, for circuit proposed in Fig. 5. In this
ISBN 973-713-063-4
In this paper is presented a technique of
increasing the dynamic range of a Gilbert cell by using
predistortion circuits at its both inputs, so that the
analog multiplier function of this circuit is preserved.
The input predistortion circuits have a transfer
characteristic of „arctanh” type which compensates
the „tanh” type nonlinearities introduced by the
Gilbert circuit. In this way, a current mode circuit is
obtained having a dynamic range wider than that of
unmodified Gilbert cell.
In the paper is shown that, by the proposed
technique, an analog multiplier circuit is obtained,
which allows the operating without distortions, for the
entire dynamic range of the input signal, in which the
inputs predistortion circuits transfer characteristics can
be considered as “arctanh” type.
The simulations made in 0.8 μm BiCMOS
technology, confirm the theoretically obtained results.
REFERENCES
[1]
[2]
[3]
[4]
45
Paul R. Gray, Robert G. Meyer, „Circuite Integrate Analogice
- Analiză úi Proiectare”, Edit. Tehnică, Bucureúti, 1999;
C. Toumazou, F. J. Lidgey, and D. G. Haigh (eds.), „Analogue
IC Design: The Current-Mode Approach”, London: Peter
Peregrinus Ltd., 1990;
D. R. Frey and Y. P. Tsividis, „Syllabically companding Log
Domain filter using dynamic biasing”, Electron. Lett., vol. 33,
no. 18, pp. 1506-1507, 1997;
Radu Gabriel Bozomitu, DănuĠ Burdia, Vlad Cehan, „Study
on “Tanh” Ideal and Lossy ELIN Integrators”, in Proc. of The
27th International Spring Seminar on Electronics Technology ISSE 2004, Sofia, Bulgaria, May 13-16, 2004.