Download 12-14-15-Intro to Relations-domain

Relations Objectives
The student will be able to:
1. identify the domain and range of a relation.
2. show relations as sets and mappings.
Vocabulary
● Relation – A relation is a general term for
any set of ordered pairs.
● Function – A function is a special type of
relation in which each member of the
domain is paired with exactly one member
of the range.
● Domain – The domain is the set of all
● x-coordinates in a set of ordered pairs.
● Range – The range is the set of all
● y-coordinates in a set of ordered pairs.
How about some more definitions?
The domain is the
set of 1st coordinates of the ordered pairs.
The range is the
set of 2nd coordinates of the ordered pairs.
A relation is a
set of ordered pairs.
Name the Domain and Range
The following set of ordered pairs has a
limited number of points.
Ex:{(2,3),(-1,0),(2,-5),(0,-3)}
Domain:  1, 0, 2 
Range:
5,  3, 0, 3
*If a number occurs more than once, you do
not need to list it more than one time.
Given the relation
{(3,2), (1,6), (-2,0)},
find the domain and range.
Domain = {3, 1, -2}
Range = {2, 6, 0}
Practice: Find the domain and
range of the following sets of
ordered pairs.
1. {(3,7),(-3,7),(7,-2),(-8,-5),(0,-1)}
Domain:{3,-3,7,-8,0}
Range:{7,-2,-5,-1}
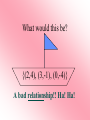
What would this be?
{(2,4), (3,-1), (0,-4)}
A bad relationship!! Ha! Ha!
The relation {(2,1), (-1,3), (0,4)}
can be shown by
1) a table.
2) a mapping.
3) a graph.
x
2
-1
0
y
1
3
4
2
-1
0
1
3
4
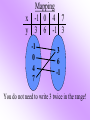
Given the following table, show the
relation, domain, range, and mapping.
x -1 0 4 7
y 3 6 -1 3
Relation = {(-1,3), (0,6), (4,-1), (7,3)}
Domain = {-1, 0, 4, 7}
Range = {3, 6, -1,}
x
y
Mapping
-1 0 4 7
3 6 -1 3
-1
0
4
7
3
6
-1
You do not need to write 3 twice in the range!
What is the domain of the relation
{(2,1), (4,2), (3,3), (4,1)}
1.
2.
3.
4.
5.
{2, 3, 4, 4}
{1, 2, 3, 1}
{2, 3, 4}
{1, 2, 3}
{1, 2, 3, 4}
Answer Now
What is the range of the relation
{(2,1), (4,2), (3,3), (4,1)}
1.
2.
3.
4.
5.
{2, 3, 4, 4}
{1, 2, 3, 1}
{2, 3, 4}
{1, 2, 3}
{1, 2, 3, 4}
Answer Now
Name the Domain and Range
From a Graph
The set of ordered
pairs may be an
infinite number of
points as described
by a graph.
Domain:{all real numbers}
Range:{y:y≥0}
Find the Domain and Range of the
Following Sets of Ordered Pairs #’s 1, 4
1. {(3,7),(-3,7),(7,-2),(-8,-5)}
D: {-8,-3,3,7}
2. f ( x)  3x 2  4
D: {All Reals} R: {y > -4}
3.
4.
2
f ( x) 
x
R: {-5,-2,7}
D: {x: x  0}
R: {y: y  0}
D: {x: x > 3}
R: {All Reals}
Objectives
The student will be able to:
1. To determine if a relation is a function.
2. To find the value of a function.
SOL: A.7aef
Designed by Skip Tyler, Varina High School
Functions
A function is a relation in which each element
of the domain is paired with exactly one
element of the range. Another way of
saying it is that there is one and only one
output (y) with each input (x).
x
f(x)
y
Function Notation
y  f x 
Input
Output
Name of
Function
Determine whether each relation
is a function.
1.
{(2, 3), (3, 0), (5, 2), (4, 3)}
2
3
5
4
f(x)
f(x)
f(x)
f(x)
3
0
2
3
YES, every domain is different!
2.
4
5
5
6
1
Determine whether the relation is
a function.
{(4, 1), (5, 2), (5, 3), (6, 6), (1, 9)}
f(x)
f(x)
f(x)
f(x)
f(x)
1
2
3
6
9
NO,
5 is paired with 2 numbers!
Is this relation a function?
{(1,3), (2,3), (3,3)}
1. Yes
2. No
Answer Now
Vertical Line Test (pencil test)
If any vertical line passes through more
than one point of the graph, then that
relation is not a function.
Are these functions?
FUNCTION!
FUNCTION!
NOPE!
Vertical Line Test
FUNCTION!
NO!
NO WAY!
FUNCTION!
Is this a graph of a function?
1. Yes
2. No
Answer Now
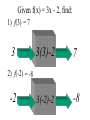
Given f(x) = 3x - 2, find:
1) f(3) = 7
3
3(3)-2
7
3(-2)-2
-8
2) f(-2) = -8
-2
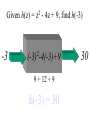
Given h(z) = z2 - 4z + 9, find h(-3)
-3
2
(-3) -4(-3)+9
9 + 12 + 9
h(-3) = 30
30
Given g(x) =
1.
2.
3.
4.
2
6
14
18
Answer Now
2
x –
2, find g(4)
Given f(x) = 2x + 1, find
-4[f(3) – f(1)]
1.
2.
3.
4.
-40
-16
-8
4
Answer Now