* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Chapter 3 - jackson.com.np
Business cycle wikipedia , lookup
Economic growth wikipedia , lookup
Non-monetary economy wikipedia , lookup
Economic democracy wikipedia , lookup
Fiscal multiplier wikipedia , lookup
Fei–Ranis model of economic growth wikipedia , lookup
Economic calculation problem wikipedia , lookup
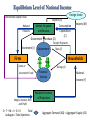
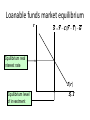
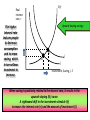
Macroeconomics & The Global Economy Term III Ace Institute of Management Chapter 3: National income-where it comes and where it goes? Instructor Sandeep Basnyat [email protected] 9841 892281 What Macroeconomics study? • Some of the foremost important questions that macroeconomics tries to investigate are: – What determines the total income in an economy? – What determines the level of production in an economy? – Who gets the income from production? – How the income is distributed among the factors of production? In general, How the economy works? Simple demonstration: Circular Flow of Income Model Equilibrium Level of National Income Foreign Sector International Capital Flows Exports (X) Market for goods and Services National Products Government Purchase (G) Consumption Expenditure (C) Imports (M) Transfer Payments Investment (I) Government Firms Loans Wages, Interest, Rent and Profit S+T+M=I+G+X Total Leakages = Total Injections Households Repay Loans or Investment Funds Taxes (T) Savings (S) Financial Services National Income (Y) Market for Factors of Production Aggregate Demand (AD) = Aggregate Supply (AS) How do the interactions occur in an economy? Our first theory: the Neo classical theory (based on classical theory) Welcome to... The place where Classical-model mechanics are made easy! P S P* D Q* Q • Its roots go back to 1776—to Adam Smith’s Wealth of Nations. • Economy was controlled by the “invisible hand” • Market system, instead of government mechanism • Buyers and sellers pursuing their own self-interest • Emphasis on competition and flexible wages/prices • Prices adjust to balance supply and demand in an economy • Economy usually maintains Full employment of resources and general equilibrium in economy How will we proceed? • Sequence of Questions and Answers: 1. What determines the level of output (or National Income) in an economy? 2. What determines the distribution of national income among factors of production? 3. What determines the factor prices? 4. What determines the demand for factor of production? An economy’s output of goods and services (GDP) depends on: (1) Quantity of inputs : Factors of Production (Capital and Labour) (2) Ability to turn inputs into output : Production Function Factors of production K = capital, tools, machines, and structures used in production L = slide 9 labor, the physical and mental efforts of workers The production function • Usually denoted Y = F (K,L) • Shows how much output (Y ) the economy can produce from K units of capital and L units of labor. • Reflects the economy’s level of technology. • Assumption: exhibits constant returns to scale (Meaning: If we increase inputs by z, output will also increase by z.) Returns to scale: a review Initially Y1 = F (K1 ,L1 ) Scale all inputs by the same factor z: K2 = zK1 and L2 = zL1 (If z = 1.25, then all inputs are increased by 25%) What happens to output, Y2 = F (K2 ,L2 ) ? • If constant returns to scale, Y2 = zY1 • If increasing returns to scale, Y2 > zY1 • If decreasing returns to scale, Y2 < zY1 Other assumptions of the model 1. Technology is fixed. 2. The economy’s supplies of capital and labor are fixed at K K slide 12 and L L Determining Output: GDP • Factors of Production and Production Function together determine the Total Output in the Economy. • Since Technology (production function) and K and L are assumed to be fixed, the output (Y) is also assumed to be fixed in an economy. Y=Y Y F (K , L ) How will we proceed? • Sequence of Questions and Answers: 1. What determines the level of output (or National Income) in an economy? – Factors of Production and the Production function 2. What determines the distribution of national income among factors of production? 3. What determines the demand for factors of production? The distribution of national income • Determined by factor prices: the prices per unit that firms pay for the factors of production. • The wage is the price of L, the rental rate is the price of K. Notation W R P W /P R /P = nominal wage = nominal rental rate = price of output = real wage (measured in units of output) [Note: P = i (inflation) reflects price level and Real Wage rate in %] = real rental rate How factor prices are determined • Factor prices are determined by supply and demand in factor markets. • Recall: Supply of each factor is fixed. • What about demand? Determination of Factor Prices Factor prices are determined by supply and demand in factor markets. Factor price (Wage or rental rate) Factor supply This vertical supply curve is a result of the supply being fixed. What about demand? Equilibrium factor price Factor demand Quantity of factor Factor Prices • Because the factor supply curve is vertical and fixed, it is the demand curve for the factors of productions which determines the distribution of income among them. • Big Question: What determines the demand for factors of production? We know that the firm will hire labor and rent capital in the quantities that maximize profit. But what are those maximizing quantities? Answer: Depends upon Marginal Revenue earned from Marginal Product of Labour and Marginal Product of Capital. Marginal product of labor (MPL) Def: The extra output the firm can produce using an additional unit of labor (holding other inputs fixed): MPL = F (K, L +1) – F (K, L) The MPL and the production function Y output F (K , L ) 1 MPL MPL As more labor is added, MPL 1 MPL 1 Slope of the production function equals MPL L labor Diminishing marginal returns • As a factor input is increased, its marginal product falls (other things equal). • Intuition: L while holding K fixed fewer machines per worker lower productivity MPL and the demand for labor Units of output Each firm hires labor up to the point where P × MPL (VMPL) = W Real wage MPL = W/P MPL, Labor demand Units of labor, L Quantity of labor demanded slide 24 The equilibrium real wage Units of output Labor supply equilibrium real wage MPL, Labor demand L The real wage adjusts to equate labor demand with supply. Units of labor, L Determining the rental rate We have just seen that MPL = W/P The same logic shows that MPK = R/P : • diminishing returns to capital: MPK as K • The MPK curve is the firm’s demand curve for renting capital. • Firms maximize profits by choosing K such that MPK = R/P . The equilibrium real rental rate Units of output Supply of capital equilibrium The real rental rate adjusts to equate demand for capital with supply. MPK, demand for capital R/P K Units of capital, K How income is distributed: total labor income = W L P R K total capital income = P MPL L MPK K If production function has constant returns to scale, then Y MPL L MPK K national income labor income capital income The income that remains after firms have paid the factors of production is the economic profit of the firms’ owners. Real economic profit is: Economic Profit = Y - (MPL × L) - (MPK × K) or to rearrange: Y = (MPL × L) + (MPK × K) + Economic Profit. Usually we find (Lumping Y and MPL into Eco. Profit): Accounting Profit = Economic Profit + (MPK x K) The Cobb-Douglas Production Function Paul Douglas observed that the division of national income between capital and labor has been roughly constant over time. Paul Douglas In other words, the total income of workers and the total income of capital owners grew at almost exactly the same rate. He then wondered what conditions might lead to constant factor shares. Cobb, a mathematician, said that the production function would need to have the property that: Capital Income = MPK × K = αY Labor Income = MPL × L = (1- α) Y Cobb–Douglas Production Function Capital Income = MPK × K = α Y Labor Income = MPL × L = (1- α) Y Production Function Cobb-Douglas α is a constant and measures capital and labors’ share of income. Cobb showed that the function with this property is: α 1- α F (K, L) = A K L A is a parameter that measures the productivity of the available technology. (Total Factor Productivity) Cobb–Douglas Production Function Cobb–Douglas Production Function: Y = F (K, L) = A Kα L1- α Differentiating, we get the Marginal product of labor: MPL = (1- α) A Kα L–α Multiply and Divide right hand side by L. Then, α –α α 1-α MPL = (1- α) [A K L ] L / L = (1- α) [A K L ]/L MPL = (1- α) Y / L Average Labour Productivity Similarly, The Marginal product of capital is: α-1 1–α MPK = α A K L or, MPK = α Y/K Average Capital Productivity Properties of the Cobb–Douglas Production Function (1) Consider the Cobb–Douglas production function: MPL = (1- α)Y/L ………….(i) MPK= α Y/ K ………………(ii) Equation (i) tells us that marginal product of the labour is proportional to output per worker (average productivity of worker). Similarly, equation (ii) states that marginal product of the capital is proportional to the output per unit of capital (average productivity of capital). In conclusion, Marginal productivity of a factor is proportional to its average productivity. Properties of the Cobb–Douglas Production Functio 2) The Cobb–Douglas production function has constant returns to scale. That is, if capital and labor are increased by the same proportion, then output increases by the same proportion as well. Proof: Consider the Cobb-Douglas Production function: F (K, L) = A Kα L1- α F(zK,zL) = A(zK)α (zL)1- α F(zK,zL) = Az α Kαz1- αL1- α F(zK,zL) = Az α z1- α KαL1- α F(zK,zL) = Az α+1- α KαL1- α F(zK,zL) = Az KαL1- α = zA KαL1- α = zF(K,L) = zY Therefore, Cobb-Douglas production function has constant returns to scale. Empirical Evidence of the Cobb–Douglas Production Fun • According to C.D. Prod. Func. : MPL α Y/L • According to Neo Classical Theory, MPL = W /P • So, MPL α W/P Growth in Labour productivity and Real Wages in US Period Labour Productivity Growth rate Real Wages Growth rate 1959-1973 1973-1995 1995-2003 2.9% 1.4% 3.0% 2.8% 1.2% 3.0% 1995-2003 2.1% 2.0% Source: US Economic Report of the President, 2005. FYI: Prepare list of some of countries that support Cobb-Douglas production function with their growth rates. How will we proceed? • Sequence of Questions and Answers: 1. What determines the level of output (or National Income) in an economy? – Factors of Production and the Production function 2. What determines the distribution of national income among factors of production? – Factor Prices 3. What determines the demand for factors of production? Demand for goods & services Components of aggregate demand: C = consumer demand for g & s I = demand for investment goods G = government demand for g & s (closed economy: no NX ) Consumption, C • def: disposable income is total income minus total taxes: Y – T • Consumption function: C = C (Y – T ) Shows that (Y – T ) C • def: The marginal propensity to consume is the increase in C caused by a one-unit increase in disposable income. • MPC = (YT ) / C = (Y T ) / C • Or, C = MPC (Y T ) The consumption function C C ( Y –T ) MPC 1 The slope of the consumption function is the MPC. Y–T Investment, I • The investment function is I = I (r ), where r denotes the real interest rate, the nominal interest rate corrected for inflation. • The real interest rate is the cost of borrowing the opportunity cost of using one’s own funds to finance investment spending. So, r I The investment function r Spending on investment goods is a downwardsloping function of the real interest rate I (r ) I Government spending, G • G includes government spending on goods and services. • G excludes transfer payments • Assume government spending and total taxes are exogenous: G G and T T Budget surpluses and deficits • When T >G , budget surplus = (T – G ) = public saving • When T <G , budget deficit = (G –T ) and public saving is negative. • When T =G , budget is balanced and public saving = 0. Equilibrium in The market for goods & services Agg. demand: Agg. supply: Equilibrium: C (Y T ) I (r ) G Y F (K , L ) Y = C (Y T ) I (r ) G The real interest rate adjusts to equate demand with supply. Equilibrium in the Financial Market: The loanable funds market A simple supply-demand model of the financial system. One asset: “loanable funds” demand for funds: investment supply of funds: saving “price” of funds: real interest rate Demand for funds: Investment The demand for loanable funds… • comes from investment: Firms borrow to finance spending on plant & equipment, new office buildings, etc. Consumers borrow to buy new houses. • depends negatively on r , the “price” of loanable funds (the cost of borrowing). Loanable funds demand curve r The investment curve is also the demand curve for loanable funds. I (r ) I Supply of funds: Saving The supply of loanable funds comes from saving: • Households use their saving to make bank deposits, purchase bonds and other assets. These funds become available to firms to borrow to finance investment spending. • The government may also contribute to saving if it does not spend all of the tax revenue it receives. Types of saving • private saving = (Y –T ) – C • public saving = T –G • national saving, S = private saving + public saving = (Y –T ) – C + T – G = Y – C – G Loanable funds supply curve r S Y C (Y T ) G National saving does not depend on r, so the supply curve is vertical. S, I Loanable funds market equilibrium r S Y C (Y T ) G Equilibrium real interest rate I (r ) Equilibrium level of investment S, I The special role of r r adjusts to equilibrate the goods market and the loanable funds market simultaneously: If L.F. market in equilibrium, then S=Y–C–G =I Add (C +G ) to both sides to get Y = C + I + G (goods market eq’m) Thus, Eq’m in L.F. market Eq’m in goods market Fiscal Policy Operations: Increase/Decrease in “G” or ‘T” An Increase in Government Purchases (G) by G : • Total demand for goods and services • General price level and demand for money (Since Total Output ( Supply) is fixed) • Savings • Interest rate • Investment level Thus, government purchases are said to crowd out investment The Crowd-out effect 1. The increase in the deficit reduces saving… 2. …which causes the real interest rate to rise… 3. …which reduces the level of investment. r S2 S1 r2 r1 I (r ) I2 I1 S, I Fiscal Policy Operations: Increase/Decrease in “G” or ‘T” A Decrease in Taxes: • Disposable (Y-T) income • Consumption (C) • Saving decreases (Since Y is fixed and C increased: Note: S =Y-C-G) • Interest rate (r) Like an increase in government purchases, tax cuts crowd out investment and raise the interest rate. Two reasons: Technological changes and Tax Policy Real interest rate, r Saving, S B A S An increase in the demand for investment goods shifts the investment schedule to the right. At any given interest rate, the amount of investment is greater. The equilibrium moves from A to B. Because the amount of saving is fixed, the increase in investment demand raises the interest rate while leaving I2 the equilibrium I1 amount of investment unchanged. Investment, Saving, I, S But, what if interest rates are even higher? S(r) Real interest rate, r The higher interest rate induces people to decrease consumption and increase saving, which in turn allows investment to increase. Upward sloping savings B I2 A I1 Investment, Saving, I, S When saving is positively related to the interest rate, it results in the upward-sloping S(r) curve. A rightward shift in the investment schedule I(r) increases the interest rate (r) and the amount of investment (I). Numerical Questions and Solutions for Practice 3) An economy's production function is cobb-douglas with parameter α =0.3. (Macroeconomics, mankiw, Pg. 73. Q. 3) a. what fractions of income do capital and labor recieve? b. suppose that immigration increases the labor force by 10 percent. what happens to total output (in percent)? c. Suppose that a technological advance raises the value of the parameter A by 10 percent. what happens to total output (in percent)? Solutions for Practice 3) An economy's production function is cobb-douglas with parameter α =0.3. (Macroeconomics, mankiw, Pg. 73. Q. 3) a. What fractions of income do capital and labor receive? 0.3 is a fraction of labor income while 0.7 is a fraction of capital income Numerical Questions and Solutions for Practice 3) An economy's production function is cobb-douglas with parameter α =0.3. (Macroeconomics, mankiw, Pg. 73. Q. 3) b. Suppose that immigration increases the labor force by 10 percent. what happens to total output (in percent)? Out put will increase 10%. Numerical Questions and Solutions for Practice 3) An economy's production function is cobb-douglas with parameter α =0.3. (Macroeconomics, mankiw, Pg. 73. Q. 3) c. suppose that a technological advance raises the value of the parameter A by 10 percent. what happens to total output (in percent)? Output increases by 10% Thank You