Download DENSITY MATRICES AND MEASUREMENTS. Slides in PPT.

Introduction to Quantum
Information Processing
Lecture 4
Michele Mosca
Overview
Von Neumann measurements
 General measurements
 Traces and density matrices and
partial traces

“Von Neumann measurement
in the computational basis”
Suppose we have a universal set of quantum
gates, and the ability to measure each qubit
in the basis { 0 , 1 }
 If we measure   ( 0 0  1 1 ) we get
b with probability α 2

b
In section 2.2.5, this is described as follows
We have the projection operators P0  0 0
and P  1 1 satisfying P  P  I
1
0
1
 We consider the projection operator or
“observable” M  0P  1P  P
0
1
1
 Note that 0 and 1 are the eigenvalues
 When we measure this observable M, the
probability of getting the eigenvalue b is
2
and we are in
Pr(b)  Φ Pb Φ  α b
that case left with the state Pb   b b  b

p(b)
b
“Expected value” of an observable
If we associate with outcome b the
eigenvalue b then the expected outcome is
 b Pr(b)
b


  b Φ Pb Φ  Φ   bPb  Φ
b
 b

 
 
 Tr  Φ   bPb  Φ   Tr M Φ Φ 
 
  b
“Von Neumann measurement
in the computational basis”
Suppose we have a universal set of quantum
gates, and the ability to measure each qubit
in the basis { 0 , 1 }

x
x
 Say we have the state
x{ 0,1 }n
 If we measure all n qubits, then we obtain
2
x with probability  x
 Notice that this means that probability of
measuring a 0 in the first qubit equals



2
x
x0 { 0,1 }n 1
Partial measurements
If we only measure the first qubit and leave
the rest alone, then we2 still get 0 with
x
probability p0  x0
{ 0,1 }
 The remaining n-1 qubits are then in the
renormalized state
x

n 1

x0 { 0,1 }n 1

p0
(This is similar to Bayes Theorem)
x
In section 2.2.5

This partial measurement corresponds to
measuring the observable
M  0 0 0 I
n 1
11 1 I
n 1
Von Neumann Measurements

A Von Neumann measurement is a type of
projective measurement. Given an
orthonormal basis { k } , if we perform a
Von Neumann measurement with respect to
{ k } of the state  
k k then
we measure k with probability

k
2
 k 
2
 k   k
 Tr  k    k
  Tr 
k
k  

Von Neumann Measurements
E.x. Consider Von Neumann measurement of
the state   ( 0   1 ) with respect to
the orthonormal basis  0  1 , 0  1 
2
2 

 Note that

  0  1

 
2 
2

   0  1
 

2 
2




We therefore get  0  1  with probability



2


2
2
Von Neumann Measurements

Note that  0  1 


  
2 
2

 0  1   *  *
 
 
2 
2

 0  1
 0  1

   
2 
2


 0  1
 Tr 
2




2

 0  1 


    

2
2



How do we implement
Von Neumann measurements?

If we have access to a universal set of
gates and bit-wise measurements in the
computational basis, we can implement Von
Neumann measurements with respect to an
arbitrary orthonormal basis { k } as
follows.
How do we implement
Von Neumann measurements?

Construct a quantum network that
implements the unitary transformation
U k  k

Then “conjugate” the measurement
operation with the operation U
 k k
U
k
prob  k
U
2
1
k
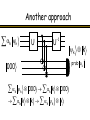
Another approach
 k k
U
U
1
prob  k
000
 
 
k
k  k
k
k
 000   k k  000
k  k   k  k  k
2
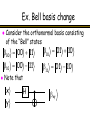
Ex. Bell basis change


Consider the orthonormal basis consisting
of the “Bell” states
00  00  11
01  01  10
10  00  11
11  01  10
Note that
x
y
H
 xy
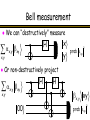
Bell measurement

We can “destructively” measure
x
H
 x,y xy
y
x, y

prob  xy
2
Or non-destructively project

x, y
x, y
xy
00
H
H
 x, y xy
prob  xy
2
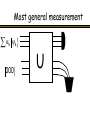
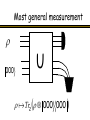
Most general measurement

k
k
000
U
Trace of a matrix
The trace of a matrix is the sum of its diagonal elements
e.g.
a00

Tr  a10
a20
a01 a02 

a11 a12   a00  a11  a22
a21 a22 
Some properties: TrxA  yB   xTrA  yTrB 
TrAB  TrBA
Tr[ ABC ]  Tr[CAB]


Tr UAU t  Tr A
Orthonormal basis { φi }
TrA   φi A φi
Density Matrices
φ  α0 0  α1 1
Notice that 0=0|, and 1=1|.
So the probability of getting 0 when measuring | is:
p(0)  0  0 
2
 0φ
2
0φ 

 0φ φ 0
 0 φ φ 0  Tr  0 φ φ 0
 Tr  0 0 φ φ   Tr  0 0 ρ

where  = || is called
the density matrix for the
state |
Mixture of pure states
A state described by a state vector | is called a
pure state.
What if we have a qubit which is known to be in the
pure state |1 with probability p1, and in |2 with
probability p2 ?
More generally, consider probabilistic mixtures of
pure states (called mixed states):
φ    φ1 , p1  ,  φ2 , p2  , ... 
Density matrix of a mixed state
…then the probability of measuring 0 is given by
conditional probability:
p(0)   pi  prob. of measuring 0 given pure state i
  pi  Tr  0 0 φi φi
i


i
 Tr  pi 0 0 φi φi
i
 Tr  0 0 ρ 
where  
p
i i
is the density matrix for the mixed
i
state 
Density matrices contain all the useful information about an
arbitrary quantum state.
i
Density Matrix
If we apply the unitary operation U to 
the resulting state is U 
with density matrix
U  U 

t
U   U
t
Density Matrix
If we apply the unitary operation U to qk , ψk
the resulting state is qk ,U ψk 
with density matrix
t
q
U
ψ
ψ
U
 k k k
k

 t
 U   qk ψk ψk U
 k

 UρU t

Density Matrix
If we perform a Von Neumann measurement
of the state     wrt a basis
containing  , the probability of
obtaining  is
 
2
Tr   

Density Matrix
If we perform a Von Neumann measurement
of the state qk , ψk 
wrt a basis containing  the probability
of obtaining 
is
q
k
k
ψk φ
2
  qk Tr  ψ k ψ k φ φ
k


 Tr   qk ψ k ψ k φ φ 
 k

 Tr ρ φ φ 

Density Matrix
In other words, the density matrix contains
all the information necessary to compute
the probability of any outcome in any
future measurement.
Spectral decomposition
Often it is convenient to rewrite the
density matrix as a mixture of its
eigenvectors
 Recall that eigenvectors with distinct
eigenvalues are orthogonal; for the
subspace of eigenvectors with a common
eigenvalue (“degeneracies”), we can
select an orthonormal basis

Spectral decomposition

In other words, we can always
“diagonalize” a density matrix so that it
is written as
ρ   pk φ k φ k
k
where φk is an eigenvector with
eigenvalue pk and φ forms an
k
orthonormal basis
 
Partial Trace
How can we compute probabilities for
a partial system?
 E.g.
 xy x y

x ,y


     xy x  y
y  x


y
  xy

py  
x y
 x py



Partial Trace
If the 2nd system is taken away and
never again (directly or indirectly)
interacts with the 1st system, then we
can treat the first system as the
following mixture


α
 E.g.  p   xy x  y  ρ
y
 x py

y






α
Trace2


xy

 p y , 
x   ρ2  Tr2 ρ


p
x
y



Partial Trace

y


α
xy

py 
x  y ρ
 x py







α
Trace2


xy

 p y , 
x   ρ2  Tr2 ρ

py
x


Tr2 ρ   p y Φ y Φ y
y
Φy  
x
α xy
py
x
Why?

the probability of measuring e.g. w in
the first register
depends only on Tr2 ρ
2
α
2
wy
  py
y
y

α wy
py
  p yTr w w Φ y Φ y

y



 Tr  w w   p y Φ y Φ y  


y



 Tr  w w Tr2 ρ 
Partial Trace

Notice that it doesn’t matter in which
orthonormal basis we “trace out” the
2nd system, e.g.
α 00  β 11  α 0 0  β 1 1
Tr2

2
2
In a different basis
1
1
 1

α 0  β 1  0  1 
α 00  β 11 
2
2 
 2
1
1
 1

α 0  β 1  0  1 

2
2 
 2
Partial Trace
1

α 0  β 1 
2

1

α 0  β 1 

2

1
Tr2
 α 0
2
1
 α 0
2
1
1

0 
1
2
2 
1
1

0 
1
2
2 




 β 1  α * 0  β* 1
 β 1  α * 0  β* 1
α 0 0β 1 1
2
2
Distant transformations don’t
change the local density matrix
Notice that the previous observation
implies that a unitary transformation on
the system that is traced out does not
affect the result of the partial trace
 I.e.
 p y Φ y U y  I  U ρ

y

 p y , Φ y
Trace2
 ρ
2
 Tr2 ρ
Distant transformations don’t
change the local density matrix
In fact, any legal quantum transformation
on the traced out system, including
measurement (without communicating
back the answer) does not affect the
partial trace
 I.e.
py , Φ y y




 p y , Φ y
Trace2
 ρ
2
 Tr2 ρ
Why??
Operations on the 2nd system should not
affect the statistics of any outcomes of
measurements on the first system
 Otherwise a party in control of the 2nd
system could instantaneously
communicate information to a party
controlling the 1st system.

Principle of implicit
measurement
If some qubits in a computation are
never used again, you can assume (if
you like) that they have been
measured (and the result ignored)
 The “reduced density matrix” of the
remaining qubits is the same

Partial Trace
This is a linear map that takes bipartite
states to single system states.
 We can also trace out the first system
 We can compute the partial trace
directly from the density matrix
description

Tr2  i k  j l
 i
k Tr  j l
 i k  l j  l j i k

Partial Trace using matrices

a00
a
 10
a20

 a30
Tracing out the 2nd system
a01 a02
a11
a12
a21 a22
a31
a32
a03 
 a00
Tr 


a13  Tr2   a10

 a20
a23 
Tr 

a33 
  a30
a01 
a02
Tr 

a11 
 a12
a21 
a22
Tr 

a31 
 a32
 a00  a11 a02  a13 


a20  a31 a22  a33 
a03  


a13  
a23  


a33  
Most general measurement

000
U
  Tr2   000 000 