Download Torque and Motion Relationships - K

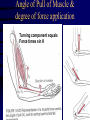
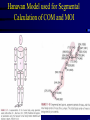
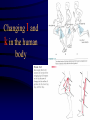
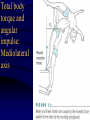
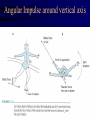
Angular Kinetics Review
• Readings:
– Hamill Ch 11 esp pp 382-410
– Kreighbaum pp 318-324, 326-331
– Adrian 33-40 (COM calculations)
• Homework problem on calculating MOI of
lower extremity will be distributed in class
Torque and Motion Relationships
• Relationship between linear and angular motion
– displacement, velocity, and acceleration
• Angular analogue of Newton’s third law (F=ma),
the instantaneous effect of a force or torque
– Torque = moment of inertia (I) X angular acc (
What is torque?
• What is moment of inertia ?
• What is radius of gyration
• Changing moment of inertia and radius of gyration in the body
Calculations using a 3-segment system
• Homework problem
What is torque, or a moment of
force?
Torque is the turning
effect of a force and is
the product of force
magnitude and moment
arm, or perpendicular
distance from the force’s
line of action to the axis
of rotation:
Angle of Pull of Muscle &
degree of force application
Turning component equals
Force times sin θ
Mechanical Advantage of Elbow
Flexors
Length of Elbow Flexors as Joint
Angle Changes
Additional problem #2, p 173: Length-tension, angle
of pull combined
Sine of
Homework #5 – Musculoskeletal machines: (due Monday, Feb 28)
Introductory problems, p 445 - # 4, 8
Additional problems, p 446 - #3
Exercise equipment problem illustrated below:
Assume force is applied
perpendicular to the bar:
a. In which position will the
exercise be easier?
b. If it takes 100 N to move
the system at position 2,
what will it take to lift it at
positions 1 and 3?
Hint: use the law of levers: Ff = Rr
and solve for F
Sample Problem #2, p 433
Example
of total
body
torques
Torque and impulse
about the center of
mass
What is the COM and why is it
important?
• What is COM (or COG) and why is it important?
– It simplifies mechanical analysis of a complicated system
– It is the point at which all of the mass of the system may be
considered to be located
– It is the only point that represents movement of the total system
The acceleration of the COM is proportional to the net force
and inversely proportional to the mass.
– It is the only point that follows a parabolic flight pattern when
free of contact with earth
– External forces through the COM cause produce only linear
motion
– External forces not through the COM (eccentric forces) create a
torque, or moment, and produce both linear and rotary motion
COM/COG Concept and Calculation
Method (Adrian pp 33-41)
• Concept of balancing segmental torques
• Segmental Calculation of COM
– General calculation method
– Information needed
• Proportionate mass of each segment
• location of COM of each segment
Segmental concept of center of mass
Hanavan Model used for Segmental
Calculation of COM and MOI
Segmental concept of center of mass
Information needed:
1. Segmental COM location
2. Segmental proportionate mass
Instantaneous effect of net torque:
Moment of Inertia (MOI) Constant
T=I

What are torque
and MOI?
Instantaneous effect of net
torque: Torque is constant
Instantaneous effect of net
torque: Ang acc ( constant
What is Moment of Inertia?
It is the resistance of a system to rotational acceleration, and is
calculated at follows:
Here, r (the radius of rotation) is equal to k (the radius
of gyration), but that is not the case with extended bodies
What is radius of
gyration (k)?
An indicator of distribution of mass
about the axis. It is the distance from
the axis to a point at which all the
mass of a system of equal mass
would be concentrated to have the
MOI equal the original system. It
is, then, the average weighted
distance of the mass of a system
to the axis.
k
35
Equivalent systems
k
35
Determining MOI & K
• Simple 3-segment system:
– I = 3mi di2 = m1 d12 + m2 d22+
m3 d32 + . . . . . . .+ mi di2
– I = mk2 ; k = (I/m).5
•
Irregularly shaped bodies
But we can’t measure all of these small masses!
Physical pendulum method of
determining MOI and K
• Suspend object at axis
• Measure mass (m), and distance from axis to COM, r
• Measure period of oscillation (T)
– Moment of inertia (I) = T2 mr * .248387 m/sec
– Radius of gyration (K) = ( I/m).5
MOI & K – Geometric Objects
Changing I and
k in the human
body
Changing I and
k in the human body
MOI around principal axes of
human body in different positions
Angular Impulse and Momentum
• Impulse-momentum relationship - effect of force or torque
applied over time
– Linear: Ft = mv
Rotational: Tt = I 
• What is angular impulse?
• Torque X time
• What is angular momentum?
• Amount of angular movement: I 
• Conservation of angular momentum
• Angular momentum is constant if net impulse is zero
Total body
torque and
angular
impulse:
Mediolateral
axis
Angular Impulse around vertical axis
What is angular momentum (L)?
Example of angular momentum
Conservation of Momentum
Conservation of Momentum