* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Independence and Conditional Probability
Survey
Document related concepts
Transcript
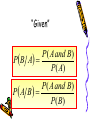
Independence and Conditional Probability Warm-Up • If P(A) = 0.3 and P(B) = 0.4 and if A and B are mutually exclusive events, find: a. • a. 0.7 P( A) b. c. P(B) • b. 0.6 P ( A or B ) • c. 0.7 d. P( A and B) • d. 0 Multiplication Rule – Independent Events…… • When 2 events are independent, the probability of both occurring is P( A and B) P( A) P( B) General Rule…… • “or” means to add • “and” means to multiply (unless it is in a contingency table and you can actually see the intersection) Example…… • If a coin is tossed twice, find the probability of getting 2 heads. • Answer: P( H and H ) P( H ) P( H ) 1 1 1 P( H and H ) 2 2 4 Example…… • A coin is flipped and a die is rolled. Find the probability of getting a head on the coin and a 4 on the die. • Answer: P( H and 4) P( H ) P(4) 1 1 1 P( H and 4) 2 6 12 Example…… • A card is drawn from a deck and replaced; then a 2nd card is drawn. Find the probability of getting a queen and then an ace. • Answer: P(Q and A) P(Q) P( A) P(Q and A) 4 4 1 52 52 169 Example…… • A box contains 3 red balls, 2 blue balls, and 5 white balls. A ball is selected and its color noted. Then it is replaced. A 2nd ball is selected and its color noted. Find the probability of a. Selecting 2 blue balls b. Selecting a blue ball and then a white ball c. Selecting a red ball and then a blue ball Answers…… a. Selecting 2 blue balls 2 2 1 P( B and B) 10 10 25 b. Selecting a blue ball and then a white ball 2 5 1 P( B and W ) 10 10 10 c. Selecting a red ball and then a blue ball 3 2 3 P( R and B) 10 10 50 Example…… • A poll found that 46% of Americans say they suffer from stress. If 3 people are selected at random, find the probability that all three will say they suffer from stress. • Answer: P( S and S and S ) P( S ) P( S ) P( S ) P(Stress) (0.46) 0.097 3 Dependent Events…… • When the outcome or occurrence of the first event affects the outcome or occurrence of the second event in such a way that the probability is changed. Examples of Dependent Events…… 1. Draw a card from a deck. Do not replace it and draw another card. 2. Having high grades and getting a scholarship 3. Parking in a no parking zone and getting a ticket Multiplication Rule – Dependent Events…… • When 2 events are dependent, the probability of both occurring is P( A and B) P( A) P( BlA ) • The slash reads: “The probability that B occurs given that A has already occurred.” Example…… • 53% of residents had homeowner’s insurance. Of these, 27% also had car insurance. If a resident is selected at random, find the prob. That the resident has both homeowner’s and car insurance. • Answer: P( H and C ) P( H ) P(ClH ) P( H and C ) (.53)(.27) .1431 Example…… • 3 cards are drawn from a deck and NOT replaced. Find the following probabilities. a. Getting 3 jacks b. Getting an ace, king, and queen c. Getting a club, spade, and heart d. Getting 3 clubs. a. Getting 3 jacks…… 4 3 2 1 P( J and J and J ) .000181 52 51 50 5525 b. Getting an ace, king, queen…… 4 4 4 8 P( A and K and Q) .000483 52 51 50 16575 c. Getting a club, spade, and heart…… 13 13 13 169 P(C and S and H ) .017 52 51 50 10200 d. Getting 3 clubs…… 13 12 11 11 P(C and C and C ) or .013 52 51 50 850 Dependent Probability Continued……Conditional Warm Up……How Likely Are You to Win the Lotto? • Many states have lotteries. The biggest jackpot, typically millions of dollars, usually comes from the Lotto game. In Lotto South, available in Georgia, Kentucky, and Virginia, six numbers are randomly sampled without replacement from the integers 1 to 49. The order of selection is not important. • Question: You buy a lottery ticket. What is the probability that it is a winning ticket, having the six numbers chosen? • The probability of winning is the probability that the 6 numbers chosen are the six that you have on your ticket. • Keep in mind that the order does not matter and that a number cannot be repeated after it has been chosen. • Find the probability of winning. Answer…… 6 5 4 3 2 1 P( All 6) 49 48 47 46 45 44 720 P( All 6) 0.00000007 10,068,347,520 • This is about 1 chance in 14 million! Insight……Provided by Wilson and Crouch 2001, p. 200 • Let’s give this small number some perspective. The chance of winning the jackpot in Lotto South (0.00000007) is…… • less than your chance of being hit by a meteorite in the next year (0.0000004). • less than your chance of dying in a tornado (0.0000002). • less than your chance of dying by a lightning strike (0.00000016). In other words…… • If you have money to spare, go ahead and play the lottery, but understand why many call it “sport for the mathematically challenged.” • By the way, the probability of winning the Lotto South is also roughly the probability that a person of average mortality will die in the next 3 minutes! • Do you still want to play? Back to Conditional Probability - Remember…… P( A and B) P( A) PB A • Algebraically change this so that it is now in the form…… “Given” P( A and B) P B A P( A) P( A and B) P A B P( B) Example…… • In Rolling Acres Housing Plan, 42% of the houses have a deck and a garage; 60% have a deck. Find the probability that a home has a garage, given that it has a deck. Answer…… P( Deck and Garage) .42 P( Deck ) .60 Find PG D • Answer: P(G and D) PG D P ( D) .42 PG D .70 .6 Example…… • At an exclusive country club, 83% of the members play bridge; 75% of the members drink champagne given that he or she plays bridge. Find the probability that members drink champagne and play bridge. Answer…… • Answer: P(bridge ) .83 P(C and B) PC B P( B) Pchamp bridge .75 P ( B and C ) .75 .83 Find P(champ and bridge ) P(C and B) (.75)(. 83) .62 Example…… • A recent survey asked 100 people if they thought women in the armed forces should be permitted to participate in combat. The results are shown in the table. Yes No Total Male 32 18 50 Female 8 42 50 Total 40 60 100 a. Find the probability that they answered yes, given that they were female. Answer: Yes No Total Male 32 18 50 Female 8 42 50 Total 40 60 100 P(Y and F ) PY F P( F ) 8 8 4 100 PY F or.16 50 50 25 100 b. Find the probability that they were male, given that they answered no. • Answer: Yes No Total Male 32 18 50 Female 8 42 50 Total 40 60 100 P( M and No) PM No P( No) 18 18 3 PM No 100 or.3 60 60 10 100