* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Light and Telescopes - Otterbein University
Survey
Document related concepts
Transcript
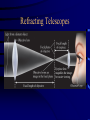
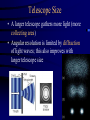
Orbital Motion = Kepler Explained Planet wants to move in a straight line of constant velocity (Newton 1) Sun’s gravitational pull forces planet into orbit by changing direction of planets velocity “Compromise”: planet moves in curved orbit It takes a stronger force to make a high speed planet move in an orbit Cannon “Thought Experiment” • http://www.phys.virginia.edu/classes/109N/more_stuff/Appl ets/newt/newtmtn.html Applications • From the distance r between two bodies and the gravitational acceleration a of one of the bodies, we can compute the mass M of the other F = ma = G Mm/r2 (m cancels out) – From the weight of objects (i.e., the force of gravity) near the surface of the Earth, and known radius of Earth RE = 6.4103 km, we find ME = 61024 kg – Your weight on another planet is F = m GM/r2 • E.g., on the Moon your weight would be 1/6 of what it is on Earth Applications (cont’d) • The mass of the Sun can be deduced from the orbital velocity of the planets: MS = rOrbitvOrbit2/G = 21030 kg – actually, Sun and planets orbit their common center of mass • Orbital mechanics. A body in an elliptical orbit cannot escape the mass it's orbiting unless something increases its velocity to a certain value called the escape velocity – Escape velocity from Earth's surface is about 25,000 mph (7 mi/sec) From Newton to Einstein • If we use Newton II and the law of universal gravity, we can calculate how a celestial object moves, i.e. figure out its acceleration, which leads to its velocity, which leads to its position as a function of time: ma= F = GMm/r2 so its acceleration a= GM/r2 is independent of its mass! • This prompted Einstein to formulate his gravitational theory as pure geometry. Telescopes From Galileo to Hubble: Telescopes use lenses and mirrors to focus and therefore collect light Rain analogy: Collect light as you collect rain Rain/light collected is proportional to area of umbrella/mirror, not its diameter Light hits Matter: Refraction • Light travels at different speeds in vacuum, air, and other substances • When light hits the material at an angle, part of it slows down while the rest continues at the original speed – results in a change of direction – Different colors bend different amounts – prism, rainbow Application for Refraction • Lenses use refraction to focus light to a single spot Light hits Matter (II): Reflection • Light that hits a mirror is reflected at the same angle it was incident from • Proper design of a mirror (the shape of a parabola) can focus all rays incident on the mirror to a single place Application for Reflection • Curved mirrors use reflection to focus light to a single spot Telescopes • Light collectors • Two types: – Reflectors (Mirrors) – Refractors (Lenses) Refracting Telescopes Reflecting Telescope Problems with Refractors • Different colors (wavelengths) bent by different amounts – chromatic aberration • Other forms of aberration • Deform under their own weight • Absorption of light • Have two surfaces that must be optically perfect Telescope Size • A larger telescope gathers more light (more collecting area) • Angular resolution is limited by diffraction of light waves; this also improves with larger telescope size Resolving Power of Telescopes Atmospheric Limitations