* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Math/Stat 360-1 - WSU Department of Mathematics
Survey
Document related concepts
Transcript
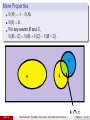
Math/Stat 360-1: Probability and Statistics, Washington State University Haijun Li [email protected] Department of Mathematics Washington State University Week 2 Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 1 / 19 Outline 1 Section 2.2: Axioms, Interpretations, and Properties of Probability 2 Section 2.3: Counting Techniques Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 2 / 19 Probability Ω: Sample space. Probability P(E): Likelihood of the random event E, E ⊆ Ω. Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 3 / 19 Probability Ω: Sample space. Probability P(E): Likelihood of the random event E, E ⊆ Ω. Basic Axioms of Probability Measures 1 2 3 0 ≤ P(E) ≤ 1 for all E ⊆ Ω. P(Ω) = 1. mutually-exclusive-1.gif (GIF Image, 411 × 275 pixels) http://www.analyzemath.com If events E1 , E2 , . . . , Ek , . . . , are Pmutually exclusive, P(E1 ∪ E2 ∪ · · · ∪ Ek ∪ · · · ) = ∞ i=1 P(Ei ). Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 3 / 19 Interpreting Probability Probability P(E): Likelihood of the random event E (relative frequency, or degree of belief, ...). Figure: p ≈ Haijun Li Pn i=1 xi /n, xi = 1 (head) xi = 0 (tail), n = number of trials Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 4 / 19 More Properties P(A0 ) = 1 − P(A). P(∅) = 0. _diagram_example_0.png (PNG Image, 484C, × 243 pixels) For any events B and P(B ∪ C) = P(B) + P(C) − P(B ∩ C). Haijun Li http://whyslopes.com/index Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 5 / 19 Example Consider testing items coming off an assembly line one by one until a defective item (labeled “F ”) is found. The sample space is Ω = {F , SF , SSF , SSSF , SSSSF , . . . , S . . S} F , . . . }. | .{z k ≥0 Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 6 / 19 Example Consider testing items coming off an assembly line one by one until a defective item (labeled “F ”) is found. The sample space is Ω = {F , SF , SSF , SSSF , SSSSF , . . . , S . . S} F , . . . }. | .{z k ≥0 Probability Model 1 2 Let P(S) = 0.99, P(F ) = 0.01. P(S . . S} F ) = (0.99)k × 0.01. | .{z k ≥0 3 P(Ω) = P∞ k =0 P(S . . S} F ) = | .{z k ≥0 Haijun Li ∞ X 0.01 = 1. 1 − 0.99 k =0 | {z } sum of a geometric series (0.99)k 0.01 = Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 6 / 19 Example In a city, 60% of all households get Internet service from the local cable company, 80% get television service from that company, and 50% get both services from that company. Let A = {getting Internet service}, B = {getting TV service}. 1 What is the probability that a randomly selected household gets at least one of these two services from the company? P(A ∪ B) = P(A) + P(B) − P(A ∩ B) = 0.6 + 0.8 − 0.5 = 0.9. Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 7 / 19 Example In a city, 60% of all households get Internet service from the local cable company, 80% get television service from that company, and 50% get both services from that company. Let A = {getting Internet service}, B = {getting TV service}. 1 What is the probability that a randomly selected household gets at least one of these two services from the company? P(A ∪ B) = P(A) + P(B) − P(A ∩ B) = 0.6 + 0.8 − 0.5 = 0.9. 2 What is the probability that a randomly selected household gets exactly one of these services from the company? P(exactly one) = P(A ∪ B) − P(A ∩ B) = 0.9 − 0.5 = 0.4. Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 7 / 19 Venn Diagrams Figure: P(A ∪ B), P(A ∩ B), P(exact one), P(A but not B) Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 8 / 19 Remarks 1 For any two events A ⊆ B, we have that P(A) ≤ P(B). Because P(B) = P(A ∪ (B ∩ A0 )) = P(A) + P(B ∩ A0 ) ≥ P(A). Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 9 / 19 Remarks 1 For any two events A ⊆ B, we have that P(A) ≤ P(B). Because P(B) = P(A ∪ (B ∩ A0 )) = P(A) + P(B ∩ A0 ) ≥ P(A). 2 P(A ∪ B ∪ C) = P(A) + P(B) + P(C) − P(A ∩ B) − P(B ∩ C) − P(C ∩ A) + P(A ∩ B ∩ C). Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 9 / 19 Probability Model of Equally Likely Outcomes Consider a sample space Ω = {ω1 , . . . , ωN }, consisting of N sample points, N ≥ 1. Assume that sample points ω1 , . . . , ωN are equally likely; that is, P(ωi ) = N1 . For any event A ⊆ Ω, P(A) = X ωi ∈A Haijun Li P(ωi ) = number of sample points in A N(A) = . N N(Ω) Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 10 / 19 Probability Model of Equally Likely Outcomes Consider a sample space Ω = {ω1 , . . . , ωN }, consisting of N sample points, N ≥ 1. Assume that sample points ω1 , . . . , ωN are equally likely; that is, P(ωi ) = N1 . For any event A ⊆ Ω, P(A) = X ωi ∈A P(ωi ) = number of sample points in A N(A) = . N N(Ω) Example: Two fair dice are rolled separately. What is the probability that the sum of the numbers is 4? P(sum is 4) = Haijun Li 3 1 = . 36 12 Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 10 / 19 The Product Rule for Ordered Pairs Count all possible pairs (O, P) The first element O can be selected in n1 ways. The second element P can be selected in n2 ways. The pair (O, P) can be selected in n1 n2 ways. Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 11 / 19 Permutations and Combinations Consider a set of n distinct objects, and 0 ≤ k ≤ n. Definition An ordered sequence of k objects is called a permutation. Pk ,n = # of all permutations of size k from the n objects. An unordered subset is called a combination. Ck ,n = # of all combinations of size k from the n objects. A more popular notation for the combination number is kn (read “n choose k ”). Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 12 / 19 Figure: P2,3 = 6 = 2 × 3 = 2!C2,3 , C2,3 = 3 Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 13 / 19 Pk ,n = k !Ck ,n , 0 ≤ k ≤ n Consider a set of n distinct objects, and 0 ≤ k ≤ n. Numbers of Permutations and Combinations The n factorial n! = n(n − 1)(n − 2) · · · (2)(1). Note that 0! = 1. Pk ,n = n(n − 1)(n − 2) · · · (n − k + 1) | {z } fill in k spots without repeating n(n − 1)(n − 2) · · · (n − k + 1)(n − k )! n! = (n − k )! (n − k )! P Ck ,n = kk!,n = (n−kn!)!k ! = kn n , and n0 = nn = 1. Note that kn = n−k = Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 14 / 19 Example Computer keyboard failures can be attributed to electrical defects or mechanical defects. A repair facility currently has 25 failed keyboards, 6 of which have electrical defects and 19 of which have mechanical defects. Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 15 / 19 Example Computer keyboard failures can be attributed to electrical defects or mechanical defects. A repair facility currently has 25 failed keyboards, 6 of which have electrical defects and 19 of which have mechanical defects. How many ways are there to randomly select 5 of these keyboards for a thorough inspection (with regard to order)? total = P5,25 = Haijun Li 25! = 25×24×23×22×21 = 6, 375, 600. (25 − 5)! Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 15 / 19 Example Computer keyboard failures can be attributed to electrical defects or mechanical defects. A repair facility currently has 25 failed keyboards, 6 of which have electrical defects and 19 of which have mechanical defects. How many ways are there to randomly select 5 of these keyboards for a thorough inspection (with regard to order)? total = P5,25 = 25! = 25×24×23×22×21 = 6, 375, 600. (25 − 5)! How many ways are there to randomly select 5 of these keyboards for a thorough inspection (without regard to order)? total = C5,25 = Haijun Li 25! 25 × 24 × 23 × 22 × 21 = = 53, 130. 20!5! 5! Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 15 / 19 Example (cont’d) Computer keyboard failures can be attributed to electrical defects or mechanical defects. A repair facility currently has 25 failed keyboards, 6 of which have electrical defects and 19 of which have mechanical defects. If a sample of 5 keyboards is randomly selected without regard to order, what is the probability that exactly two have an electrical defect? Prob = Haijun Li N(A) C2,6 C3,19 15 × 969 = = = 0.2736. N C5,25 53, 130 Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 16 / 19 Example A production facility employs 20 workers on the day shift, 15 workers on the swing shift, and 10 workers on the graveyard shift. A quality control consultant is to select 6 of these workers for in-depth interviews. Selections are made at random without replacement. Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 17 / 19 Example A production facility employs 20 workers on the day shift, 15 workers on the swing shift, and 10 workers on the graveyard shift. A quality control consultant is to select 6 of these workers for in-depth interviews. Selections are made at random without replacement. How many selections result in all 6 workers coming from the day shift? 20 20! = 38, 760. = 6 14!6! Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 17 / 19 Example A production facility employs 20 workers on the day shift, 15 workers on the swing shift, and 10 workers on the graveyard shift. A quality control consultant is to select 6 of these workers for in-depth interviews. Selections are made at random without replacement. How many selections result in all 6 workers coming from the day shift? 20 20! = 38, 760. = 6 14!6! What is the probability that all 6 selected workers will be from the day shift? 20 N(A) 6 = 0.0048. = 45 Prob = N(Ω) 6 Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 17 / 19 Example (cont’d) What is the probability that all 6 selected workers will be from the same shift? 15 10 20 N(A) 6 6 6 Prob = = 45 + 45 + 45 = 0.0054. N(Ω) 6 6 6 Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 18 / 19 Example (cont’d) What is the probability that all 6 selected workers will be from the same shift? 15 10 20 N(A) 6 6 6 Prob = = 45 + 45 + 45 = 0.0054. N(Ω) 6 6 6 What is the probability that at least two different shifts will be represented among the selected workers? Prob = 1 − Prob that all 6 will be from the same shift = 1 − 0.0054 = 0.9946. Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 18 / 19 Example (cont’d) What is the probability that at least one of the shifts will be unrepresented in the sample of workers? Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 19 / 19 Example (cont’d) What is the probability that at least one of the shifts will be unrepresented in the sample of workers? A = {day shift will be unrepresented in the sample} B = {swing shift will be unrepresented in the sample} C = {graveyard shift will be unrepresented in the sample} A ∩ B = {all 6 selected from the graveyard shift} A ∩ C = {all 6 selected from the swing shift} B ∩ C = {all 6 selected from the day shift} A ∩ B ∩ C = ∅. Haijun Li Math/Stat 360-1: Probability and Statistics, Washington State University Week 2 19 / 19 Example (cont’d) What is the probability that at least one of the shifts will be unrepresented in the sample of workers? A = {day shift will be unrepresented in the sample} B = {swing shift will be unrepresented in the sample} C = {graveyard shift will be unrepresented in the sample} A ∩ B = {all 6 selected from the graveyard shift} A ∩ C = {all 6 selected from the swing shift} B ∩ C = {all 6 selected from the day shift} A ∩ B ∩ C = ∅. P(A∪B∪C) = P(A)+P(B)+P(C)−P(A∩B)−P(A∩C)−P(B∩C) 25 30 35 10 15 20 = Haijun Li 6 45 6 + 6 45 6 + 6 45 6 − 6 45 6 − 6 45 6 − 6 45 6 Math/Stat 360-1: Probability and Statistics, Washington State University = 0.2885. Week 2 19 / 19