Download Math/Stat 360-1 - WSU Department of Mathematics

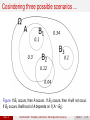
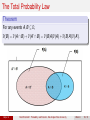
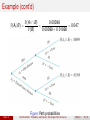
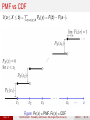
Math/Stat 360-1: Probability and Statistics,
Washington State University
Haijun Li
[email protected]
Department of Mathematics
Washington State University
Week 3
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
1 / 31
Outline
1
Section 2.4: Conditional Probability
2
Section 2.5: Independence
3
Section 3.1: Random Variables
4
Section 3.2: Probability Distributions for Discrete Random
Variables
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
2 / 31
Probabilistic Modeling
Three Basic Ingredients:
1
Sample space Ω
2
Events E
3
Probability measure P(E)
Motivation for Conditional Probability Measures
It should be easier to estimate probabilities if more relevant
information is given.
The probability P(E) can be calculated by analyzing what
could possibly happen under various possible scenarios.
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
3 / 31
Cosindering three possible scenarios ...
Figure: If B1 occurs, then A occurs. If B3 occurs, then A will not occur.
If B2 occurs, likelihood of A depends on P(A ∩ B2 ).
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
4 / 31
Definition
Let A and B be two events with P(B) > 0. The conditional
probability of A given that B occurs is defined as
P(A|B) :=
Haijun Li
P(A ∩ B)
, A, B ⊆ Ω.
P(B)
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
5 / 31
Example
In a city, 60% of all households get Internet service from the
local cable company, 80% get television service from that
company, and 50% get both services from that company. Let
A = {getting Internet service}, B = {getting TV service}.
1
What is the probability that a randomly selected household
gets Internet service given that it gets TV service from that
company?
P(A ∩ B)
0.5
P(A|B) =
=
= 0.625.
P(B)
0.8
2
What is the probability that a randomly selected household
gets TV service given that it gets Internet service from that
company?
P(A ∩ B)
0.5
P(B|A) =
=
= 0.833.
P(A)
0.6
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
6 / 31
The Multiplication Rule
Theorem
1
For any two events A1 , A2 ⊆ Ω,
P(A1 ∩ A2 ) = P(A1 |A2 )P(A2 ) = P(A2 |A1 )P(A1 ).
2
For any three events A1 , A2 , A3 ⊆ Ω,
P(A1 ∩ A2 ∩A3 ) = P(A3 | A1 ∩ A2 )P(A1 ∩ A2 ) =
| {z }
| {z } | {z }
B
B
B
P(A3 |A1 ∩ A2 )P(A2 |A1 )P(A1 ).
3
This can be extended to multiple events.
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
7 / 31
Example
Four individuals have responded to a request by a blood bank
for blood donations, and their blood types are unknown.
Suppose only type O+ is desired and only one of the four
actually has this type.
If the potential donors are selected in random order for
typing, what is the probability that at least three individuals
must be typed to obtain the desired type?
Let A = {first type is not O+}, B = {second type is not O+}
P(at least three individuals are typed) = P(A ∩ B)
= P(B|A)P(A) =
Haijun Li
2 3
× = 0.5.
3 4
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
8 / 31
Example (cont’d)
Four individuals have responded to a request by a blood bank
for blood donations, and their blood types are unknown.
Suppose only type O+ is desired and only one of the four
actually has this type.
What is the probability that type O+ is typed on the third
donor?
Let C = {third type is O+}.
P(O+ is typed on the third donor) = P(C|A ∩ B)P(B|A)P(A)
=
Haijun Li
1 2 3
× × = 0.25.
2 3 4
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
9 / 31
The Total Probability Law
Theorem
For any events A, B ⊆ Ω,
P(B) = P(A ∩ B) + P(A0 ∩ B) = P(B|A)P(A) + P(B|A0 )P(A0 ).
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
10 / 31
Remark
Events {A1 , A2 , . . . , Ak } constitute a partition of sample
space Ω if they are mutually exclusive and ∪ki=1 Ai = Ω.
For any event B,
P(B) =
k
X
i=1
P(Ai ∩ B) =
k
X
P(B|Ai )P(Ai ).
i=1
where P(B|Ai ), i = 1, . . . , k , are usually “easier” to calculate.
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
11 / 31
Example
An individual has 3 different email accounts. 70% of her
messages come into account #1, whereas 20% come into
account #2 and the remaining 10% into account #3. Of the
messages into account #1, only 1% are spam, whereas the
corresponding percentages for accounts #2 and #3 are 2% and
5%, respectively. What is the probability that a randomly
selected message is spam?
Let Ai = {message is from account # i}, i = 1, 2, 3, B = {message
is spam}. It follows from the total probability law that
P(B) = P(B|A1 )P(A1 ) + P(B|A2 )P(A2 ) + P(B|A3 )P(A3 )
= 0.01 × 0.7 + 0.02 × 0.2 + 0.05 × 0.1 = 0.016.
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
12 / 31
Bayes’ Rule
Theorem
Let {A1 , A2 , . . . , Ak } be a partition of sample space Ω. For any
events B ⊆ Ω,
P(Aj |B) =
Haijun Li
P(Aj ∩ B)
P(B|Aj )P(Aj )
= Pk
, j = 1, . . . , k .
P(B)
i=1 P(B|Ai )P(Ai )
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
13 / 31
Example
An individual has 3 different email accounts. 70% of her
messages come into account #1, whereas 20% come into
account #2 and the remaining 10% into account #3. Of the
messages into account #1, only 1% are spam, whereas the
corresponding percentages for accounts #2 and #3 are 2% and
5%, respectively.
What is the probability that a randomly selected message is
from account #1 given that it is spam?
Let Ai = {message is from account # i}, i = 1, 2, 3, B = {message
is spam}. It follows from Bayes’ rule that
P(B|A1 )P(A1 )
P(A1 |B) =
P(B|A1 )P(A1 ) + P(B|A2 )P(A2 ) + P(B|A3 )P(A3 )
0.01 × 0.7
0.007
=
=
= 0.4375.
0.01 × 0.7 + 0.02 × 0.2 + 0.05 × 0.1
0.016
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
14 / 31
Example (Incidence of a rare disease)
Only 1 in 1000 adults is afflicted with a rare disease for which a
diagnostic test has been developed. The test is such that when
an individual actually has the disease, a positive result will occur
99% of the time, whereas an individual without the disease will
show a positive test result only 2% of the time. If a randomly
selected individual is tested and the result is positive, what is the
probability that the individual has the disease?
Let A1 = individual has the disease, A2 = individual does not
have the disease, and B = positive test result.
P(A1 ) = 0.001, P(A2 ) = 0.999, P(B|A1 ) = 0.99, P(B|A2 ) = 0.02.
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
15 / 31
Example (cont’d)
P(A1 |B) =
P(A1 ∩ B)
0.00099
=
= 0.047.
P(B)
0.00099 + 0.01998
Figure: Path probabilities
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
16 / 31
“Learning” via Bayes’ Rule
Let H be an event of interest, and E be an event representing
the evidence.
Figure: P(H) is updated to P(H|E).
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
17 / 31
Independence
Two events A and B are independent if P(A|B) = P(A).
The Product Form: Two events A and B are independent is
equivalent to that P(A ∩ B) = P(A)P(B).
Independence and mutually exclusive are different. Two
mutually exclusive events are in fact highly dependent.
If A and B are independent, then
P(A ∪ B) = P(A) + P(B) − P(A ∩ B) = P(A) + P(B) − P(A)P(B).
Definition
Events A1 , A2 , . . . , An are mutually independent if for any subset
{i1 , . . . , ik } ⊆ {1, . . . , n},
P(Ai1 ∩ · · · ∩ Aik ) = P(Ai1 ) × · · · × P(Aik ).
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
18 / 31
Example
Consider a system consisting of two components #1 and #2.
Assume that components work independently of one another
and P(component works) = 0.9.
Components #1 and #2 are connected in series, so that
system works iff both #1 and #2 work. Calculate
P(system works).
P(system works) = P(#1)P(#2) = 0.92 = 0.81.
Components #1 and #2 are connected in parallel, so that
system works iff either #1 or #2 works. Calculate
P(system works).
P(system works) = P(#1) + P(#2) − P(#1)P(#2)
= 0.9 + 0.9 − 0.92 = 0.99.
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
19 / 31
Example (cont’d)
Consider a system consisting of two components #1 and #2.
Assume that components work independently of one another
and P(component works) = 0.9.
Components #1 and #2 are connected in parallel. Given
that the system fails, what is the probability that component
#1 fails?
P(component #1 fails | system works) =
=
Haijun Li
P(#2 works)
P(system works)
0.9
= 0.909.
0.99
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
20 / 31
Example
Consider the system of 4 components. Components 1 and 2 are
connected in parallel; 3 and 4 are connected in series. If
components work independently of one another and
P(component works) = 0.9, calculate P(system works).
P(1 or 2) = 0.99, P(3 and 4) = 0.81.
P(system works) = 0.99 + 0.81 − (0.99)(0.81) = 0.9981.
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
21 / 31
Random Variables
Random variable (RV): A function defined on the sample
space.
Example: Toss a coin three times. Let N = number of
heads in three tosses.
N(TTH) = 1, N(HHH) = 3, N(HTH) = 2, N(TTT ) = 0.
Example: Sample a product from an assembly line. Let
T = lifelength of the item.
Discrete random variable: Its values are limited to discrete
points (i.e., finite or countably infinite) on the real line.
Continuous random variable: It takes on continuous
measurements.
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
22 / 31
Example
Toss a fair coin three times. The sample space =
{HHH, HHT , HTH, THH, TTH, THT , HTT , TTT }.
Let N denote the number of heads in three tosses.
P(N = 0) = 1/8, P(N = 1) = 3/8,
P(N = 2) = 3/8, P(N = 3) = 1/8.
Table: Probability Masses
N=x
0
P(N = x) 1/8
Haijun Li
1
3/8
2
3
3/8 1/8
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
23 / 31
Discrete Random Variables
The distribution of a discrete random variable X is
described by the probability mass function (PMF)
p(xi ) = P(X = xi ), for all the possible values xi of X .
Distribution of RV X : Likelihoods or relative frequencies of
various values of X .
Properties of PMF
1
2
0 ≤ p(x) ≤ 1.
P
all x’s p(x) = 1.
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
24 / 31
Example
Consider a group of five potential blood donors, a, b, c, d, and e,
of whom only a and b have type O+ blood. Five blood samples,
one from each individual, will be typed in random order until an
O+ individual is identified. Let RV Y = the number of typings
necessary to identify an O+ individual. Then the PMF of Y is
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
25 / 31
Example (cont’d)
Figure: The line graph for the PMF
Figure: The histogram for the PMF
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
26 / 31
Cumulative Distribution Function =
Cumulative Frequency
Cumulative Distribution Function (CDF) of X
F (x) = P(X ≤ x) =
X
p(y ).
y :y ≤x
1
2
3
F (x) is step-wise, non-decreasing.
0 ≤ F (x) ≤ 1.
F (x) → 1 as x → +∞.
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
27 / 31
PMF vs CDF
P(a ≤ X ≤ b) =
P
y :a≤y ≤b
PX (y ) = F (b) − F (a−).
Figure: PX (x) = PMF, FX (x) = CDF
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
28 / 31
Example (Five Blood Samples)
Let RV Y = the number of typings necessary to identify an O+
individual. The PMF of Y is given by
The CDF of Y is given by

0




 0.4
0.7
F (x) =


0.9



1
Haijun Li
if x < 1
if 1 ≤ x < 2
if 2 ≤ x < 3
if 3 ≤ x < 4
if 4 ≤ x
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
29 / 31
Example (Geometric Distribution)
Consider testing items coming off an assembly line one by one
until a defective item (labeled “F ”) is found. Let X be the number
of testing items necessary to find the first defective item. If
P(F ) = p, find the PMF and CDF of X .
Let “S” denote a non-defective item, and so P(S) = 1 − p.
The PMF of X : p(k ) = P(X = k ) = (1 − p)k −1 p, k ≥ 1.
For the CDF, for any positive integer x ≥ 1,
F (x) = P(X ≤ x) =
X
k ≤x
=
Haijun Li
p(k ) =
x
X
(1 − p)k −1 p
k =1
1 − (1 − p)x
p = 1 − (1 − p)x .
p
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
30 / 31
Example (cont’d): Geometric CDFs
Haijun Li
Math/Stat 360-1: Probability and Statistics, Washington State University
Week 3
31 / 31