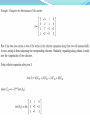Download File

Determinants
 In this chapter we will study “determinants” or, more
precisely, “determinant functions.” Unlike real-valued
functions, such as f(x)=x2, that assign a real number to
a real variable x, determinant functions assign a real
number f(A) to a matrix variable A.
 Although determinants first arose in the context of
solving systems of linear equations, they are rarely
used for that purpose in real-world applications.
Theorem:
det(A) is a function from the set of 2 x 2 matrices to the real
numbers having the properties:
1 0
𝒂 𝒃
𝒄 𝒅
 𝑑𝑒𝑡
=1
𝒅𝒆𝒕
= −𝒅𝒆𝒕
𝒄 𝒅
𝒂 𝒃
0 1
 If you exchange two rows the determinant changes sign ↑
 The determinant is linear in each row ↓
Another Theorem:
For any positive integer n there is exactly one function
det(A) from the set of all n x n matrices to the real
numbers called the determinant of A having 3
properties:
1) The determinant of the identity matrix is 1
2) If you exchange 2 rows of A the determinant chages
sign.
3) The determinant is linear in each row.
Theorem: Determinants of
Elementary Matrices
(*)
 Minor Determinants is computing the determinant as
a linear combination of the determinants of smaller
sub-matrices.
 In (*) we deleted the first row of A in each of the 3 sub-
matrices and then used the entries from the first
column as the coefficients of minor determinants. The
resulting formula for the determinant of A is called its
Cofactor Expansion along the first row.
Examples:
1) The identity matrix is a diagonal matrix.
2) A square matrix in REF is upper triangle.
3) Elementary matrices that scale a row are diagonal
matrices.
4) Elementary matrices that add a multiple of an upper
row to a lower row are lower trianglar. Elementary
matrices that add a multiple of an lower row to a
upper row are lower trianglar.
5) Elementary matrices that exchange 2 rows are
neither upper or lower trianglar,
Theorem:
1) The transpose of a lower triangular matrix is upper
triangular and the transpose of an upper triangular
matrix is lower triangular.
2) A product of lower triangular matrices is lower triangular
and the product of upper triangular matrices is upper
triangular.
3) A triangular matrix is invertible if and only if all of its
diagonal entries are non-zero.
4) The inverse of an invertible lower triangular matrix is
lower triangular and the inverse of an invertible upper
triangular matrix is upper triangular.
Proof of Theorem:
LU Decomposition:
Example:
Step repeated
Theorem:
If A is an invertible matrix that can be reduced to REF
without row exchanges then there exists an invertible
lower triangular matrix L and invertible upper triangular
matrix U with 1s along the diagonal such that
A = LU
The factorization is called an LU-Decomposition of A.
Solving Systems of Linear Equations
using LU-Decomposition method:
Questions to Get Done
Suggested practice problems (11th edition)
 Section 2.1 #15-21 odd
 Section 2.2 #5-21 odd
 Section 2.3 #7-17 odd