Download ppt

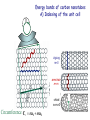
Electrons in Solids
Carbon as Example
• Electrons are characterized by quantum numbers which can be
measured accurately, despite the uncertainty relation.
In a solid these quantum numbers are:
Energy:
E
Momentum: px,y,z
• E is related to the translation symmetry in time (t),
px,y,z to the translation symmetry in space (x,y,z) .
• Symmetry in time allows t =   E = 0 (from E · t ≥ h/4 )
Symmetry in space allows x =   p = 0 (from p · x ≥ h/4 )
• The quantum numbers px,y,z live in reciprocal space since p = ћ k .
Likewise, the energy E corresponds to reciprocal time. Therefore,
one needs to think in reciprocal space-time, where large and small
are inverted (see Lecture 6 on diffraction).
Use a single crystal
to simplify calculations
Unit cell
Instead of calculating the electrons for an infinite crystal,
consider just one unit cell (which is equivalent to a molecule).
Then add the couplings to neighbor cells via hopping energies.
The unit cell in reciprocal space is called the Brillouin zone.
Two-dimensional energy bands of graphene
E
Empty
EFermi
Occupied
K
Empty
=0
kx,y
M
K
M
Occupied
In two dimensions one has
the quantum numbers E, px,y .
Energy band dispersions (or
simply energy bands) plot E
vertical and kx , ky horizontal.
Energy bands of graphite (including  bands)
E
The graphite energy bands
resemble those of graphene,
but the , * bands broaden
due to the interaction between
the graphite layers (via the pz
orbitals).
*
*
pz
EFermi
px,y

pz

sp2
s
kx,y
Brillouin
zone


M
K
Energy bands of carbon nanotubes
A) Indexing of the unit cell
zigzag
m=0
armchair
n=m
chiral
nm0
Circumference Cr  na1  ma2
Energy bands of carbon nanotubes
B) Quantization along the circumference
Analogous to Bohr’s quantization
condition one requires that an
integer number n of electron
wavelengths fits around the
circumference of the nanotube.
(Otherwise the electron waves
would interfere destructively.)
This leads to a discrete number
of allowed wavelengths n and
k values kn = 2/n . (Compare
the quantization condition for a
quantum well, Lect. 2, Slide 9).
Two-dimensional k-space gets
transformed into a set of onedimensional k-lines (see next).
k
(A) Wrapping vectors (red) and allowed wave vectors kn (purple) for (3,0) zigzag, (3,3) armchair, and (4,2)
chiral nanotubes. If the metallic K-point lies on a purple line, the nanotube is metallic, e.g. for (3,0) and (3,3).
The (4,2) nanotube does not contain K, so it has a band gap. All armchair nanotubes (n,n) are metallic, since
the purple line through  contains the two orange K-points. Note that the purple lines are always parallel to the
axis of the nanotube, since the quantization occurs in the perpendicular direction around the circumference.
(B) Band structure of a (6,6) armchair nanotube, including the metallic K-point (orange dot). Each band
corresponds to a purple quantization line. Their spacing is Δk = 2 / 1 = 2 / circumference = 1/ radius .
Energy bands of carbon nanotubes
C) Relation to graphene
(5,5) Nanotube
folded
in half
Two steps lead from the  bands of graphene to those
of a carbon nanotube:
Graphene
1) The gray continuum of
2D bands gets quantized
into discrete 1D bands.
2) The unit cell and Brillouin
zone need to be converted
from hexagonal (graphene)
to rectangular (armchair
nanotube. Thereby, energy
bands become back-folded.
EF



K
M
(for the dashed band)
Two classes of solids
Carbon nanotubes cover both
Energy
Metals
empty levels
• Energy levels are continuous .
• Electrons need very little energy
to move  electrical conductor
filled levels
Semiconductors, Insulators
empty levels
• Filled and empty energy levels
separated by an energy gap.
• Electrons need a lot of energy
to move  poor conductor .
are
gap
filled levels
Measuring the quantum numbers of electrons in a solid
The quantum numbers E and k can both be measured by angle-resolved
photoemission. This is an elaborate use of the photoelectric effect which
was explained as quantum phenomenon by Einstein :
Photon in
Electron outside
Electron inside
Energy and momentum of an emitted photoelectron are measured.
Use energy conservation to get the electron energy:
Electron energy outside the solid
− Photon energy
= Electron energy inside the solid
Energy bands of graphene from photoemission
Evolution of the in-plane band dispersion
with the number of layers
In-plane k-components
(single layer graphene)
Evolution of the perpendicular band
dispersion with the number of layers:
N monolayers produce N discrete k-points.
Ohta et al., Phys. Rev. Lett, 98, 206802 (2007)
The density of states D(E)
D(E) is defined as the number of states per energy interval.
Each electron with a distinct wave function counts as a state.
D(E) involves a summation over k, so the k-information is thrown out.
While energy bands can only be determined directly by angle-resolved photoemission,
there are many techniques available for determining the density of states.
By going to low dimensions in nanostructures one can enhance the density of states at
the edge of a band (E0). Such “van Hove singularities” can trigger interesting phenomena, such as superconductivity and magnetism.
Tailoring the Density of States
by Confinement to
Density
of States
Nanostructures
Adjust
via d
Potential Well
1D
3D
EFermi
d
Energy
Density of states of a single nanotube
from scanning tunneling spectroscopy
Calculated
Density of
States
Scanning
Tunneling
Spectroscopy
(STS)
Cees Dekker, Physics Today, May 1999, p. 22.
Optical spectra of nanotubes
with different diameter, chirality
Simultaneous data for fluorescence (x-axis) and
absorption (y-axis) identify the nanotubes completely.
Bachilo et al.,
Science 298,
2361 (2002)
Need to prevent nanotubes from touching each other for sharp levels
Sodium
Dodecyl
Sulfate
(SDS)
O'Connell et al, Science 297, 593 (2002)
Quantized Conductance
Dip nanotubes into a liquid metal
(mercury, gallium). Each time an
extra nanotube reaches the metal.
the conductance increases by the
same amount.
The conductance quantum:
G0 = 2 e2/h  1 / 13k
(Factor of 2 for spin ,  )
Each wave function = band = channel
contributes G0 . Expect 2G0 = 4 e2/h
for nanotubes, since 2 bands cross EF
at the K-point. This is indeed observed
for better contacted nanotubes (Kong et
al., Phys. Rev. Lett. 87, 106801 (2001)).
Cees Dekker, Physics Today, May 1999, p. 22.
Limits of Electronics from
Information Theory
Conductance per channel: G = G0•T
Energy to switch one bit:
E = kBT • ln2
Time to switch one bit:
t = h/E
Energy to transport a bit: E = kBT • d/c
(G0 = 2 e2/h, transmission T1)
(distance d, frequency )
Birnbaum and Williams, Physics Today, Jan. 2000, p. 38.
Landauer, Feynman Lectures on Computation .
Energy scales in carbon nanotubes
~20 eV
Band width ( + * band)
~ 1 eV
Quantization along the circumference ( k = 1/r )
~ 0.1 eV
Coulomb blockade (charging energy ECoul = Q/eC )
Quantization energy along the axis ( k|| = 2/L )
~ 0.001 eV
Many-electron effects (electron  holon + spinon)