Download Impedance Z

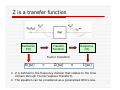
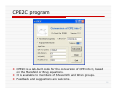
Introduction to EIS and
Conversion of CPE into C
Dr. Zack Qin
The Blind Men and the Elephant
… Is very like a wall!
… Is very like a spear!
… Is very like a snake!
… Is very like a tree!
… Is very like a fan!
… Is very like a rope!
…….
Not one of them has seen!
J. G. Saxe (1816-1887)
1
Z is a transfer function
Excitation
E(t)
Transfer
Function
Response
I(t)
Fourier transform
E(jω)
=
Z(jω)
x
I(jω)
™ Z is defined in the frequency domain that relates to the time
domain through Fourier/Laplace Transform.
™ The equation can be considered as a generalized Ohm’s law.
2
Z is a complex function
Z (ω ) = Z ' (ω ) + jZ " (ω ) = Z (ω ) e − jθ (ω )
Z ' (ω ) = Re[ Z ( jω )]
Z " (ω ) = Im[ Z ( jω )]
Z”
Z (ω ) = Z ' (ω ) 2 + Z " (ω ) 2
⎛ Z " (ω ) ⎞
θ (ω ) = arctan ⎜ − '
⎟
ω
Z
(
)
⎝
⎠
Z’
™ Z is described by pair-functions, Z’ and Z”, or |Z| and θ.
™ Z’(ω), Z”(ω), |Z(ω)|, and θ(ω) are real functions.
™ Other related immittance functions:
Admittance
Modulus
Dielectric constant
Y = Z-1
M = jωC0Z
ε = (jωC0Z)-1
3
Element impedances
Resistance (Ω)
R=E/I
⇒
ZR = R
™ Dissipation of energy (Ohm’s law): I in phase with E
™ For a uniform area resistor: R = ρ L/A
Capacitance (F)
C=
dQ
I
=
dE ( dE dt )
1
jω C
⇒
ZC =
⇒
Z L = jω L
™ Storage of charge (Coulomb’s law): I leads E.
™ For a parallel-plate capacitor: C = εε0 A/d
Inductance (H)
dΦ
E
L=
=
dI
( dI dt )
™ Storage of magnetic energy (Faraday’s law): I lags E.
™ Inductive behaviours are not normally observed in electrochemical
systems, but can be attributed to adsorption phenomenon.
4
Kirchhoff’s rules
™ Conservation of energy -- the sum of potential differences across
each element around any closed circuit loop must be zero.
™ Conservation of charge -- the sum of the currents entering any
junction must equal the sum of the currents leaving that
junction.
Impedances in series:
E1
Z1
I
E2
Z2
I
E1 + E2
= Z1 + Z 2
Z=
I
Impedances in parallel:
E
Z1
Z2
I1
I2
1 I1 + I 2 1
1
=
= +
Z
E
Z1 Z 2
5
Randles circuit
Cdl
Rs
Rct
Z ' = Rs +
Z"= −
Rct
1 + (ωCdl Rct ) 2
Rs = lim Z
ω →∞
ωCdl R
1 + (ωCdl Rct ) 2
⎛ Z '− R −
⎜
s
⎝
2
ct
Rct
2
⎞ + ( Z ") 2 = ⎛ Rct ⎞
⎜ 2⎟
2 ⎟⎠
⎝
⎠
Rct = lim Z − lim Z
ω →0
2
ω →∞
log Cdl = − log Z (ω = 1)
6
Time constant
™ The time constant (relaxation time), τ, characterizes the response
of a first order linear time-invariant system. It represents the
time required to reach (1-1/e) of its asymptotic value in a step
response, or 1/e of its initial value in a impulse response.
™ The time constant will remain the same for the same system
regardless of the starting conditions.
™ RC circuit: τ = RC, and RL circuit: τ = L/R, regardless of series
circuits or parallel circuits.
Vin − VC
dVC
=C
R
dt
Vin ( t = 0) = 0, Vin ( t > 0) =V0
⎯⎯⎯⎯⎯⎯⎯⎯
→ VC (t ) = V0 (1 − e
−t
RC
)
7
Characteristic frequency
1
ω c = 1τ =
RC
™ ωc is the physical property of a RC circuit.
™ ωc is defined in the frequency domain, while τ is defined in the
time domain.
™ ωc is the resonance frequency at which –Z” is maximum.
™ ωc is the cutoff frequency at which energy entering the system
begins to be attenuated or reflected instead of transmitted.
8
Other frequencies
™ The inflection frequency, ωθ, is the frequency at which the absolute
value of the phase angle θ reaches maximum.
™ The breakpoint frequencies, ω1 and ω2, are frequencies at θ=-45°.
™ While ωc is the property of a RC circuit, ωθ and ω1,2 are the
properties of Randles circuit.
Relationships to ωc
Rct
ωθ = ωc 1 +
Rs
ω1,2
ωc ⎛
Rs
Rs2 ⎞
= ⎜1 ± 1 − 4
−4 2 ⎟
⎜
2 ⎝
Rct
Rct ⎟⎠
ωθ
9
Constant phase element
Z CPE = [Y0 ⋅ ( jω )α ]−1
(θ = απ 2 )
= p/2 - θ
™ CPE is a phenomenological term first used by Brug in 1984. It
is an empirical impedance that its phase angle is independent
of frequency.
™ CPE is often related to frequency dispersion attributed to
surface inhomogeneities and distributed time constants.
™ CPE obeys Kramers-Kronig relations provided that |α| ≤ 1.
™ The physical justification of CPE is not obvious except on the
following circumstances:
α
1
0
-1
0.5
Y0
C
1/R
1/L
1/√2σ
10
Conversion of CPE into C
™ While the use of CPE usually increases the “goodness of the
fit”, the physical meaning of the CPE should be discussed.
™ Avoid using CPE. If this is inevitable, the causes of the nonidealism should be identified.
™ CPE is often used to describe non-ideal capacitive behaviour.
However, the amplitude Y0 is not a capacitance.
™ The dimension of Y0 is secα/Ω, while that of C is F or sec/Ω.
™ Small deviations of the exponent α from 1 can lead to large
computational errors of capacitance.
™ To obtain a trustworthy value of α, the testing frequencies
should be at least a decade lower than ωc.
™ For conversion into C, the exponent α must be in the range of
0.8-1. Otherwise, CPE won’t represent a capacitor.
™ The conversion of Y0 into C has been controversial. At least
three distinct equations have been proposed.
CPE is not a capacitor, and Y0 is not capacitance
11
Brug conversion
⎡ ⎛ 1 1 ⎞ ⎤
C = ⎢Y0 ⎜ + ⎟ ⎥
⎢⎣ ⎝ Rs Rct ⎠ ⎥⎦
α −1
1α
™ It applies to Randles circuit with no more than one τ.
™ It depends on the solution conductivity. This dispersion is largest
when Rs dominates over Rct.
™ It obtained by comparing impedance (admittance) with relaxation
analysis.
1
⎡
⎤
1
−
⎢ 1 + R R + R Y ( jω )α ⎥
⎣
⎦
s
ct
s 0
∞
⎤
1 ⎡
1
Y=
F
s
ds
1
−
(
)
⎥
∫ 1 + Rs Rct + jωτ 0 exp(s)
Rs ⎢⎣ −∞
⎦
Y=
1
Rs
G.J. Brug, et al, J Electroanal. Chem. 176 (1984), 275-295.
12
Mansfeld conversion
α −1
C = Y0ωc
™ It applies to an individual R||C, regardless how many branches
are nested in the circuit.
™ No dependency on the solution conductivity.
™ The derivation was based on
the fact that Z’ is independent
of α at ωc, which itself is also
independent of α. Therefore,
-6000
12000
a=0.8.z
a=0.9.z
a=1.z
Z =
1
2
2α
c
Y ω
2
0
1
= 2 2
ωc C
C.H. Hsu and F. Mansfeld, Corrosion, 57 (2001), 747-748.
-5000
8000
-4000
6000
-3000
4000
-2000
2000
-1000
0
10-3
10-2
10-1
100
101
102
103
Z''
1
1
=
Y0 ( jωc )α
jωc C
Z'
10000
0
104
Frequency (Hz)
13
Extension of Mansfeld
With Warburg
Nested R||C
14
Westing/Mertens conversion
Y0ωθα −1
C=
sin(απ 2)
™ First described in the PhD thesis of Westing (1992), and later
modified by Mertens (1997).
™ The derivation assumed that ZCPE(ωθ) = ZC(ωθ), where ωθ is the
inflection frequency.
1
1
=
Y0 ( jω )α
jωC
(ω = ωθ )
⎛ απ
= cos ⎜ −
⎝ 2
⎞
⎛ απ ⎞
⎟ + j sin ⎜ −
⎟
⎠
⎝ 2 ⎠
j
−α
™ Ilevbare and Scully proposed the use of the equation, but Hsu
and Mansfeld claimed the equation is incorrect.
S.F. Mertens, et al, Corrosion, 53 (1997), 381-388.
15
CPE2C program
™ CPE2C is a lab-built code for the conversion of CPE into C, based
on the Mansfeld or Brug equations.
™ It is available to members of Shoesmith and Wren groups.
™ Feedback and suggestions are welcome.
16
Use of CPE2C
™ Fit EIS spectrum with an appropriate equivalent circuit according
the spectrum and the system under investigation.
™ Identify the origin of the CPE (capacitive, diffusive, porous, a
combination of them, or even a wrong circuit).
™ For non-ideal capacitive behaviour, select the conversion method:
Mansfeld
• The ωc is the characteristic frequency associated with that
R||C to be converted. Note the angular frequency ω = 2πf.
• The calculated C must satisfy the condition when comparing
with the measured ωc,
1/Tolerance < RCωc < Tolerance
• Independent of solution conductivity at all.
Brug
• Apply to a Randles circuit, a blocking electrode, and
geometry-induced frequency dispersion.
• Conversion depends on solution conductivity.
™ The exponent α must be in the range of 0.8-1.
17
Example
CPE2C
Mansfeld
R (Ω)
ωc (rad/s)
Y0
α
C (F)
CPE-1
100
5384.4
10-5
0.8
1.794e-6
CPE-2
250
4.6572
0.001
0.9
8.574e-4
Brug
Rs (Ω)
R1
Y0
α
C (F)
A
10
100
10-5
0.8
9.764e-7
B
1
100
10-5
0.8
5.609e-7
18