Download Given

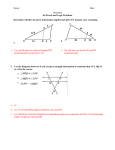
#12
A proof convinces an audience that a conjecture is true for ALL cases (situations)
that fit the conditions of the conjecture. For example, "If a polygon is a triangle
on a flat surface, then the sum of the measures of the angles is 180˚." Because we
proved this conjecture in chapter two, it is always true. There are many formats
that may be used to write a proof. This course explores three of them, namely,
paragraph, flow chart, and two-column.
Example
If BD is a perpendicular bisector of AC , prove that ∆ABC isosceles.
Paragraph proof
To prove that ∆ABC is isosceles, show that BA BC . We can
do this by showing that the two segments are corresponding
parts of congruent triangles.
Since BD is perpendicular to AC , mBDA = mBDC = 90°.
B
A
D
C
Since BD bisects AC , AD CD . With BD BD (reflexive property), ∆ADB ∆CDB
by SAS.
Finally, BA BC because corresponding parts of congruent triangles are congruent.
Therefore, ∆ABC must be isosceles since two of the three sides are congruent.
Flow chart proof
Given: BD is the perpendicular bisector of AC
ADB BDC
AD CD
BD BD
bisector
reflexive
!CBD !ABD
Two-Column Proof
iven:
BD is a bisector of AC .
BD is perpendicular to AC .
Prove: ∆ ABC is isosceles
Statement
BD bisects
Reason
AC
.
Given
BD AC
Given
AD CD
Def. of bisector
ADB and BDC
are right angles
Def. of perpendicular
!ABC is isosceles
ADB BDC
All right angles are .
Definition of isosceles
BD BD
Reflexive property
∆ABD ∆CBD
S.A.S.
AB CB
∆'s have parts
∆ABC is isosceles
Def. of isosceles
SAS
BA BC
GEOMETRY Connections
!s have parts
31
In each diagram below, are any triangles congruent? If so, prove it. (Note: It is good
practice to try different methods for writing your proofs.)
B
1.
2.
B
B
3.
D
C
A
A
A
D
C
C
D
4.
E
5.
D
C
D
6.
E
C
B
F
A
B
D
A
B
C
A
Complete a proof for each problem below in the style of your choice.
7. Given: TR and MN bisect each other.
Prove: NTP MRP
8. Given: CD bisects ACB ; 1 2
Prove: CDA CDB
A
N
R
1
C
P
T
D
2
M
B
9. Given: AB || CD , B D ,
AB CD
Prove: ABF CED
10. Given: PG SG , TP TS
Prove: TPG TSG
P
C
T
E
B
F
G
D
S
A
11. Given: OE MP , OE bisects MOP 12. Given: AD||BC , DC||BA
Prove: MOE POE
Prove: ADB CBD
M
C
D
E
P
32
A
B
Extra Practice
13. Given: AC bisects DE , A C
Prove: ADB CEB
14. Given: PQ RS , R S
Prove: PQR PQS
D
R
C
B
Q
P
A
E
S
15. Given: S R , PQ bisects
SQR
Prove: SPQ RPQ
TU GY, KY||HU ,
16. Given:
KTTG , HG TG
Prove: K H
S
K
P
Q
U
T
G
Y
R
H
17. Given: MQ||WL , MQ WL
Consider the diagram below.
Prove: ML||WQ
B
D
W
Q
A
E
C
18. Is BCD EDC ? Prove it!
L
M
19. Is AB DC ? Prove it!
20. Is AB ED ? Prove it!

Answers
1. Yes
BAD BCD
Given
BDC BDA
right 's are 
2. Yes
B E
Given
BD BD
BCA  BCD
BC  CE
vertical s are 

Given
Reflexive
! ABD  ! CBD
AAS
GEOMETRY Connections
! ABC ! DEC
ASA
33
3. Yes
AC CD
Given
BCD BCA
4. Yes
right 's are =
BC BC
AD BC
Given
BA CD
CA CA
Reflexive
! ABC ! CDA
! ABC ! DBC
SSS
SAS
5.
Not necessarily. Counterexample:
Given
Reflexive
6. Yes
BCEF
ACFD
Given
Given
! ABC! DEF
HL
7. NP MP and TP RP by definition of bisector. NPT MPR because vertical angles are equal.
So, NTP MRP by SAS.
8. ACD BCD by definition of angle bisector. CD CD by reflexive so CDA CDB by ASA.
9. A C since alternate interior angles of parallel lines congruent so ABF CED by ASA.
10. TG TG by reflexive so TPG TSG by SSS.
11. MEO PEO because perpendicular lines form right angles MOE POE by angle
bisector and OE OE by reflexive. So, MOE POE by ASA.
12. CDB ABD and ADB CBD since parallel lines give congruent alternate interior angles.
DB DB by reflexive so ADB CBD by ASA.
13. DB EB by definition of bisector. DBA EBC since vertical angles are congruent. So
ADB CEB by AAS.
14. RQP SQP since perpendicular lines form congruent right angles. PQ PQ by reflexive so
PQR PQS by AAS.
15. SQP RQP by angle bisector and PQ PQ by reflexive, so SPQ RPQ by AAS.
16. KYT HUG because parallel lines form congruent alternate exterior angles.
TY+YU=YU+GU so TY GU by subtraction. T G since perpendicular lines form
congruent right angles. So KTY HGU by ASA. Therefore, K H since  triangles
have congruent parts.
17. MQL WLQ since parallel lines form congruent alternate interior angles. QL QL by
reflexive so MQL WLQ by SAS so WQL MLQ since congruent triangles have
congruent parts. So ML || WQ since congruent alternate interior angles are formed by
parallel lines.
18. Yes
19. Not necessarily.
Reflexive
20. Not necessarily.
SAS
34
Extra Practice