* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Circular Motion and Gravitation
Inertial frame of reference wikipedia , lookup
Coriolis force wikipedia , lookup
Jerk (physics) wikipedia , lookup
Brownian motion wikipedia , lookup
N-body problem wikipedia , lookup
Fictitious force wikipedia , lookup
Fundamental interaction wikipedia , lookup
Classical mechanics wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Mass versus weight wikipedia , lookup
Hunting oscillation wikipedia , lookup
Centrifugal force wikipedia , lookup
Seismometer wikipedia , lookup
Work (physics) wikipedia , lookup
Equations of motion wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Classical central-force problem wikipedia , lookup
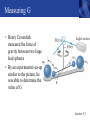
Nicholas J. Giordano www.cengage.com/physics/giordano Circular Motion and Gravitation Introduction • Circular motion • Acceleration is not constant • Cannot be reduced to a one-dimensional problem • Examples • Car traveling around a turn • Parts of the motion of a roller coaster • Centrifuge • The Earth orbiting the Sun • Gravitation • Explore gravitational force in more detail • Look at Kepler’s Laws of Motion • Further details about g Introduction Uniform Circular Motion – Overview • Circular motion is an example of accelerated motion • It can be analyzed in terms of acceleration and forces • A problem-solving strategy can be applied in a manner similar to one- and two-dimensional motion approaches Section 5.1 Uniform Circular Motion • Assume constant speed • The direction of the velocity is continually changing • The vector is always tangent to the circle • Uniform circular motion is circular motion at constant speed Section 5.1 Uniform Circular Motion, cont. • Examine one trip around the track • The distance traveled is the circumference of the track • The period of the motion, T is • r is the radius of the track • v is the speed of the motion • The period does not depend on the location on the object • The speed depends on the radius of the circle of motion and so depends on location • Speeds are fastest at the outside edge Section 5.1 Centripetal Acceleration • Although the speed is constant, the velocity is not constant • Direction of acceleration • Always directed toward the center of the circle • This is called the centripetal acceleration • Centripetal means “centerseeking” • Magnitude of acceleration Section 5.1 Circular Motion and Forces • Newton’s Second Law can be applied to circular motion: • The force must be directed toward the center of the circle • The centripetal force can be supplied by a variety of physical objects or forces • The “circle” does not need to be a complete circle Section 5.1 Centripetal Force Example • The centripetal acceleration is produced by the tension in the string • If the string breaks, the object would move in a direction tangent to the circle at a constant speed Section 5.1 Problem Solving Strategy – Circular Motion • Recognize the principle • If the object moves in a circle, then there is a centripetal force acting on it • Sketch the problem • Show the path the object travels • Identify the circular part of the path • Include the radius of the circle • Show the center of the circle • Selecting a coordinate system that assigns the positive direction toward the center of the circle is often convenient Section 5.1 Problem Solving Strategy, cont. • Identify the principles • Find all the forces acting on the object • A free body diagram is generally useful • Find the components of the forces that are directed toward the center of the circle • Find the components of the forces perpendicular to the center • Apply Newton’s Second Law for both directions • The acceleration directed toward the center of the circle is a centripetal acceleration Section 5.1 Problem Solving Strategy, final • Solve for the quantities of interest • Check your answer • Consider what the answer means • Does the answer make sense Section 5.1 Centripetal Acceleration Example: Car • A car rounding a curve travels in an approximate circle • The radius of this circle is called the radius of curvature • Forces in the y-direction • Gravity and the normal force • Forces in the x-direction • Friction is directed toward the center of the circle Section 5.1 Car Example, cont. • Since friction is the only force acting in the x-direction, it supplies the centripetal force • Solving for the maximum velocity at which the car can safely round the curve gives Section 5.1 Example: Car on Banked Curve • The maximum speed can be increased by banking the curve • Assume no friction between the tires and the road • The car travels in a circle, so the net force is a centripetal force • There are forces due to gravity and the normal force acting on the car Section 5.1 Banked Curve, cont. • There is a horizontal component of the normal force • Letting the horizontal be the x-direction • The speed at which the car will just be able to negotiate the turn without sliding up or down the banked road is • When θ = 0, v = 0 and you cannot turn on a very icy unbanked road without slipping Section 5.1 Examples of Circular Motion • When the motion is uniform, the total acceleration is the centripetal acceleration • Remember, this means that the speed is constant • The motion does not need to be uniform • Then there will be a tangential acceleration included • Many examples can be analyzed by looking at the two components Section 5.2 Non-Uniform Circular Motion • If the speed is also changing, there are two components to the acceleration • One component is tangent to the circle, at • The other component is directed toward the center of the circle, ac Section 5.2 Circular Motion Example: Vertical Circle • The speed of the rock varies with time • At the bottom of the circle: • Tension and gravity are in opposite directions • • The tension supports the rock (mg) and supplies the centripetal force Section 5.2 Vertical Circle Example, cont. • At the top of the circle: • Tension and gravity are in the same direction • Pointing toward the center of the circle • Section 5.2 Vertical Circle Example, Final • There is a minimum value of v needed to keep the string taut at the top • Let Ttop = 0 • • If the speed is smaller than this, the string will become slack and circular motion is no longer possible Circular Motion Example: Roller Coaster • The roller coaster’s path is nearly circular at the minimum or maximum points on the track • There is a maximum speed at which the coaster will not leave the top of the track: • • If the speed is greater than this, N would have to be negative • This is impossible, so the coaster would leave the track Section 5.2 Circular Motion Example: Artificial Gravity • Circular motion can be used to create “artificial gravity” • The normal force acting on the passengers due to the floor would be • If N = mg it would feel like the passengers are experiencing normal Earth gravity Section 5.2 Circular Motion Example: Centrifuge • A centrifuge is a device used in many laboratories • It can be used to separate particles or molecules • Or remove them • The effective force causes the particle to move to the bottom of the test tube • Similar to artificial gravity • To someone outside of the test tube, the particle appears to spiral Section 5.2 Frames of Reference and the Centrifuge • The stationary observer is in an inertial reference frame • He can apply Newton’s Second Law • His interpretation is correct • • There is no actual force acting on the particle The force FAG is a fictitious force • The observer moving with the particle is in an accelerated frame • He cannot apply Newton’s Second Law • He thinks there is a force acting on the particle • They agree on the particle’s motion Section 5.2 Newton’s Law of Gravitation • In many cases, the orbits of planets and moons are approximately circular • The Law of Gravitation plays a key role in physics • It allows us to calculate and understand the motion of a wide variety of objects • Newton’s application of his law of gravitation to motion of planets and moons was the first time physics was successfully applied to describe the motion of the solar system • • Showed that the laws of physics apply to all objects Had an effect on how people viewed the universe Section 5.3 Newton’s Law of Gravitation, Equation • Law states: There is a gravitational attraction between any two objects. If the objects are point masses m1 and m2, separated by a distance r the magnitude of the force is Section 5.3 Law of Gravitation, cont. • Note that r is the distance between the objects • G is the Universal Gravitational Constant • G = 6.67 x 10-11 N . m2/ kg2 • The gravitational force is always attractive • Every mass attracts every other mass • The gravitational force is symmetric • The magnitude of the gravitational force exerted by mass 1 on mass 2 is equal in magnitude to the force exerted by mass 2 on mass 1 • The two forces form an action-reaction pair Section 5.3 Gravitation and the Moon’s Orbit • The Moon follows an approximately circular orbit around the Earth • There is a force required for this motion • Gravity supplies the force Section 5.3 Notes on the Moon’s Motion • We assumed the Moon orbits a “fixed” Earth • It is a good approximation • It ignores the Earth’s motion around the Sun • The Earth and Moon actually both orbit their center of mass • We can think of the Earth as orbiting the Moon • The circle of the Earth’s motion is very small compared to the Moon’s orbit Section 5.3 Gravitation and g • Assuming a spherical Earth, we can consider all the mass of the Earth to be concentrated at its center • The value of r in the Law of Gravitation is just the radius of the Earth Section 5.3 Gravitation and g, cont. • Since the weight of a person is also the gravitational force between the person and the Earth, we can find the value of g: • The value of g is a function only of the Earth’s mass and radius, and the value of G Section 5.3 Gravitation Force From The Earth – Assumptions • We assumed • A spherical Earth • That the gravitational force could be calculated as if all the mass of the Earth was located at its center • Assumptions are true as long as the density of the object is spherically symmetric • The object has a constant density • The object’s density varies with depth as long as the density depends only on the distance from the center Section 5.3 Measuring G • Henry Cavendish measured the force of gravity between two large lead spheres • By an experimental set-up similar to the picture, he was able to determine the value of G Section 5.3 More About Gravity – Newton’s Apple • G is a constant of nature • Gravity is a weak force • Much smaller than typical normal or tension forces • Gravity is considered the weakest of the fundamental forces of nature • Newton showed the motion of celestial bodies and the motion of terrestrial motion are caused by the same force and governed by the same laws of motion Section 5.3a Johannes Kepler • Kepler studied results of other astronomer’s measurements of portions of the Moon, planets, etc. • He found the motion of the Moon and planets could be described by a series of laws • Now called Kepler’s Laws of Planetary Motion • Kepler’s Laws are mathematical rules inferred from the available information about the motion in the solar system • Kepler could not give a scientific explanation or derivation of his laws • Newton’s Laws of Motion and Gravitation give the explanation Section 5.4 Kepler’s First Law of Planetary Motion • Planets move in elliptical orbits • The Sun is at one focus • This was very different from the previous idea that the planets moved in perfect circles with the Sun at the center Section 5.4 Kepler’s First Law of Planetary Motion, Planetary Orbits Section 5.4 Kepler’s Second Law of Planetary Motion • A line connecting a planet to its sun sweeps out equal areas in equal times as the planet moves around its orbit • If the time required for the planet to sweep out area A1 is equal to the time to sweep out A2, the areas will be equal • The planet’s speed will be slowest when it is farthest from its sun and fastest when it is closest Section 5.4 Kepler’s Third Law of Planetary Motion • The square of the period of an orbit is proportional to the cube of the orbital radius • For simplicity, apply to a circular orbit • Period is T and the gravitational force supplies a centripetal force • Also applies to satellites with MSun replaced by Mplanet Section 5.4 Orbit Examples • Low Earth orbit • International Space Station, for example • T ~ 90 minutes • r ~ 6.66 x 106 m • Geosynchronous Orbit • T = 1 day • Always above the same position above the Earth • r = 4.2 x 107 m Section 5.4 Kepler’s Laws and Orbits, Summary • Kepler’s Three Laws of planetary motion apply to all types of gravitationally produced orbital motion • Different motions result from different ways of initially setting objects into motion • For example, launching a satellite to the east into an equatorial orbit takes advantage of the speed of the Earth’s rotation Section 5.4 Tides • Tides are the fluctuations of the level of the Earth’s oceans • Tides are due to the Moon’s gravitational force on the oceans • Also exerts a force on the solid Earth • The bulge in the ocean is due to the slightly greater force acting on the side of the Earth facing the Moon • Due to the dependence of gravity on distance • The bulge is a high tide Section 5.5 Tides, cont. • One high tide occurs when the Moon is directly overhead • The acceleration of the water closest to the Moon is more than that of the rest of the Earth • Twelve hours later the acceleration of the solid Earth is more than the ocean water on the farther side • There are generally two high tides per day, 12 hours apart Section 5.5 Tides, final • The Sun also affects tides • Its effects are smaller than the Moon’s • When the Sun and the Moon are aligned and on the same of the Earth, the tide is higher than when produced by the Moon alone Section 5.5 Inverse Square Law • Newton’s Law of Gravitation is an example of what is called in mathematics an inverse square law • A number of other forces in nature are also inverse square laws • Force between two electric charges, for example • How can you explain why so many forces follow this pattern? Section 5.6 Field Lines • Imagine that an object possesses gravitational field lines that emanate from it • Also imagine that the number of lines is proportional to the mass • When the lines intersect another object, there is a force on that object directed parallel to the lines Section 5.6 Field Lines, cont. • Since the force lines emanate in three-dimensional space, the number of lines that intercept the second object falls off with distance as 1/r2 • The result implies that gravity follows an inverse square law because we live in three-dimensional space • It also means we should expect other forces described by the field line picture to have the same inverse square dependence Section 5.6 Field Lines, final • No one has devised a way to see the line • You can observe the resulting force that the lines are presumed to cause • Gravitational force is also an example of “action at a distance” • Newton’s Law of Gravitation tells us that action at a distance does occur • The Law doesn’t tell us how it occurs • The field line picture was invented to answer this “how” question Section 5.6 Mass • The mass in the gravitational force is sometimes called gravitational mass • The mass in Newton’s Second Law of Motion is called inertial mass • The gravitational mass of an object is exactly equal to its inertial mass • Needed the theories of relativity to explain why they were equal • Also tells us that a photon of light will be accelerated by gravity • Even though it is a massless particle Section 5.6