Download Algebra_1A_files/Lecture 1-4

Ch 1.4 – Equations &
Inequalities
Objective:
To recognize symbols, variables, and
types of sentences used in algebra.
Definitions
Expression
An expression involves numbers and/or variables and math operators
(+, --, *, /) and only one side of an equation.
For example: 5x + 2
Equation
A statement formed by placing an equal sign (=) between two expressions.
For example: 5(x) + 2 = 12
Inequality
A statement formed by placing a “greater than” sign (>)
or a “less than” sign (<) between two expressions.
For example: 10 + 2 > 0
10 + 2 < 20
Symbols
Equalities
= Equals (the same)
Inequalities
< Is less than
> Is greater than
 Is less than or
equal to
≥ Is greater than
or equal to
= Not equal to
Give three solutions to each sentence below.
1) x > 10
Samples: 11, 15, 34
2) x + 3  7
Samples:
4, -8, 0
3) 5 - x < 0
Samples:
6, 7, 10
4) 2x  1  3
Samples:
3, 4, 7
Use mental math to solve each equation.
1) x + 4 = 9
{5}
2) 5 - x = 2
{3}
3) 2x + 3 = 17 { 7 }
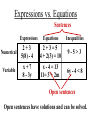
Expressions vs. Equations
Sentences
Expressions
Numerical
Variable
2+3
5(8) - 4
x+7
8 - 3y
Equations
2+3=5
4 + 2(3) = 10
x - 4 = 13
11= 3 + 2m
Inequalities
9-5>3
6y - 4 < 8
Open sentences
Open sentences have solutions and can be solved.
Open sentences have solutions and can be solved.
Variable Equations
4+m=7
-4
-4
m=3
One Solution
Variable Inequalities
5 + y < 91
-5
-5
y < 86
Infinite
Solutions
Identify each as an expression, sentence,
open sentence, equation, or inequality.
1) 3x + 5 = 11
Sentence, open sentence, equation
2) 7 < 2(5) + 3
Sentence, inequality
3) 5x - 2
Expression
4) 6m + 2 > 3
Sentence, open sentence, inequality