* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Basics of atmospheric dynamics
Newton's laws of motion wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Fluid dynamics wikipedia , lookup
Analytical mechanics wikipedia , lookup
Classical central-force problem wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Routhian mechanics wikipedia , lookup
N.Kämpfer
Atmospheric
dynamics
Basics of atmospheric dynamics
Introduction
Equation of motion
continuity equation
N. Kämpfer
Primitive equations
Geostrophic wind
Institute of Applied Physics
University of Bern
20. / 23. March 2012
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
Outline
Introduction
N.Kämpfer
Equation of motion
continuity equation
Primitive equations
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
Geostrophic wind
Thermal wind
Thermal wind
Vorticity
Circulation
Absolute vorticity
Vorticity
Circulation
Absolute vorticity
Rossby waves
Rossby waves
Introduction
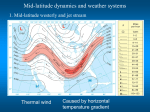
In an atmosphere with horizontal temperature gradients,
density gradients will be generated and as such pressure
gradients. These in turn will lead to a circulation of the
atmosphere.
The circulation of the atmosphere of a planet is a key
component of its climate. In case of ♁ for example:
I Atmospheric motions carry heat from the tropics to the
pole
I winds transport humidity from the oceans to the land
I Distribution of most chemical species in the atmosphere
is the result of transport processes
I
I
I
I
O3 is mainly produced in equatorial regions but is
transported polewards
H2 O enters the middle atmosphere in the tropics and is
moved toward the poles
CFCs are released in industrial areas and generate
ozone-holes in polar regions
Aerosols are produced in industrial areas and affect
regions far away
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
Introduction
Air motions are strongly constrained by:
I
I
Density stratification
→ gravitational force resists vertical displacement
Earth rotation
→ Coriolis force is a barrier against meridional
displacements
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
Transport occurs at a variety of spatial and temporal scales.
In case of ♁:
I global
I
synoptic ≈ 1000km
→ e.g. high and low pressure systems
I
mesoscale ≈ 10 - 1000km
→ e.g.fronts
I
small scale
→ e.g. planetary boundary layer
Geostrophic wind
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
Introduction
In order to describe the dynamical behavior of the
atmosphere, we treat it as a fluid
→Fundamental equations of fluid mechanics must be used
N.Kämpfer
Atmospheric
dynamics
Introduction
Circulation of a planet’s atmosphere is governed by three
basic principles:
Equation of motion
continuity equation
Primitive equations
1. Newton’s law of motion
Geostrophic wind
2. Conservation of energy → first law of thermodynamics
Thermal wind
3. Conservation of mass → equation of continuity
Vorticity
plus the equation of state
Circulation
Absolute vorticity
Rossby waves
In using these laws we must consider that we are operating
in a rotating frame of reference!
→ we have to consider centrifugal and the Coriolis force
Coriolis force
Example: Planes heading to Miami from Toronto and Quito
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
Coriolis effect causes things moving toward the poles to lead
the earth’s rotation because they are headed into regions
where the earth’s rotational speed is slower
⇒ They are deflected to the east
Coriolis effect causes things moving toward the equator to
lag the earth’s rotation because they are headed into regions
where the earth’s rotational speed is faster
⇒ They are deflected to the west
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
Coordinate system
It is practical to use a spherical coordinate system with origin
at the center of the Earth to describe dynamical aspects
The coordinate system is rotating together with the planet
N.Kämpfer
Atmospheric
dynamics
Introduction
λ
φ
z
R
longitude in easterly direction
latitude in northerly direction
geometric altitude
radius of planet, r = R + z
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
u = r cos φdλ/dt zonal component of wind velocity ~v
measured towards the east
v = rdφ/dt
meridional component of wind velocity ~v
measured towards the north
w = dz/dt
vertical component of ~v
Real forces
Real forces entering in the equation of motion are:
1. Pressure gradient force, F~p
Whenever there is a gradient in pressure the resulting
force per mass is given by
1~
F~p = − ∇p
ρ
F~p ⊥ isobars, directed from higher to lower pressure
Distance of isobars → measure for the pressure gradient
Typical values for pressure gradient for ♁:
→ ca. 1mb per 8m in vertical direction and
1mb per 10km in horizontal direction
2. Gravity force, F~G
~ = −~g
F~G = −∇Φ
3. Frictional force, F~R is nearly proportional to wind speed
F~R = −a~v
important in planetary boundary layer
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
Equation of motion without rotation
Considering all forces: general equation of motion per mass
d~v
~p + F
~R + F
~G
=F
dt
N.Kämpfer
Atmospheric
dynamics
Neglecting friction
Introduction
1~
d~v
= − ∇p
− ~g
dt
ρ
Equation of motion
continuity equation
Primitive equations
Considering vertical direction only
Geostrophic wind
1 ∂p
dw
= −g −
dt
ρ ∂z
Thermal wind
Vorticity
In case there is no vertical acceleration, i.e. in equilibrium we
arrive at
∂p
= −g ρ
∂z
This is the hydrostatic equilibrium
d
dt ,
What means
Circulation
Absolute vorticity
Rossby waves
i.e. the time derivative in a fluid?
Material derivative
Consider an atmospheric parameter ψ, like p, T or ~v
I
ψ is a vector or a scalar field variable
I
ψ depends on location and time ψ = ψ(x, y , z, t)
I
ψ is measured by fixed instruments
N.Kämpfer
Atmospheric
dynamics
Introduction
Equations so far however are valid for a moving air parcels
Equation of motion
dψ
dt
Primitive equations
What is the time derivative
→ total derivative
of a moving air parcel?
continuity equation
Geostrophic wind
Thermal wind
dψ
∂ψ dx
∂ψ dy
∂ψ dz
∂ψ dt
=
+
+
+
dt
∂x dt
∂y dt
∂z dt
∂t dt
Vorticity
Circulation
Absolute vorticity
Rossby waves
I
partial derivatives (e.g.
I
derivatives like
∂ψ
∂y )
dy
dt are valid for particles
v , dz
dt = w are the components
= u, dy
dt =
velocity ~v of the particle
I dx
dt
are valid for the field ψ
of the
Eulerian and Lagrangeian point of view
dψ
dt
∂ψ dx
∂ψ dy
∂ψ dz
∂ψ dt
+
+
+
∂x dt
∂y dt
∂z dt
∂t dt
∂ψ
∂ψ
∂ψ ∂ψ
= u
+v
+w
+
∂x
∂y
∂z
∂t
∂ψ
~
=
+ ~v · ∇ψ
∂t
=
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
dψ
dt ,
the so called material
Total change of ψ with time
derivative, is built up of
I change of time at fixed position, i.e. local: ∂ψ
∂t
~
I advective change ~
v · ∇ψ
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
→ Eulerian point of view
→ Lagrangeian point of view
Keep in memory:
d
dt
=
∂
∂t
For the velocity ~v this leads to
~
+ ~v · ∇
d~v
dt
=
∂~v
∂t
~v
+ ~v · ∇~
Apparent forces in a rotating reference system
The centrifugal force is showing up in a rotating reference
frame
→ its effect is absorbed“ in the gravitational force
”
An object moving with velocity ~v in a plane perpendicular to
the axis of rotation experiences an apparent force, called
~C .
Coriolis force, F
~ C = 2~v × ω
F
~
The angular velocity is for ♁: ω = Ω = 7.3 · 10−5 sec−1
The Coriolis force in horizontal direction can be written as
d~
v
h
~C h =
F
= −f ~k × ~vh
dt C
~k is a unit vector in z-direction where f is called
Coriolis-Parameter
f = 2Ω sin ϕ
f is equal to zero at the equator and has a maximum at the
poles f = ±1.46 · 10−4 sec−1
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
Apparent forces
The Coriolis force per mass for zonal velocity, u, and
geographic latitude ϕ is
dv
= −2Ωu sin ϕ = −fu
dt
and analogue for meridional direction
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
du
= 2Ωv sin ϕ = fv
dt
continuity equation
Primitive equations
Geostrophic wind
Thermal wind
I
I
I
The Coriolis force is acting normal to the direction of
motion
→ to the right in the northern hemisphere
→ to the left in the southern hemisphere
As the force is acting normal to the direction of motion
no work is performed
The force vanishes at the equator and is maximum at
the poles
Vorticity
Circulation
Absolute vorticity
Rossby waves
Equation of motion with rotation
Considering all forces: general equation of motion per mass
d~v
~p + F
~c + F
~R + F
~G
=F
dt
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
resp.
d~v
1~
~ × ~v − a~v + ~g
= − ∇p
− 2Ω
dt
ρ
continuity equation
Primitive equations
Geostrophic wind
We remember
Thermal wind
d~v
∂~v ~ =
+ ~v · ∇ ~v
dt
∂t
→ nonlinear in ~v → difficult to forecast atmospheric state
Vorticity
In atmospheric dynamics usually spherical coordinates are
used what makes look the equations more complicated
Circulation
Absolute vorticity
Rossby waves
Equation of motion in spherical coordinates
The whole set in spherical coordinates without friction
N.Kämpfer
du
uv
uw
1
∂p
=
tan ϕ −
+ 2Ω sin ϕv − 2Ω cos ϕw −
dt
r
r
ρr cos ϕ ∂λ
dv
u2
uw
1 ∂p
= − tan ϕ −
− 2Ω sin ϕu −
dt
r
r
ρr ∂ϕ
dw
u2 + v 2
1 ∂p
=
+ 2Ω cos ϕu − g −
dt
r
ρ ∂r
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
Thermal wind
In the Lagrangian frame we have to take care of the total
Vorticity
Circulation
Absolute vorticity
derivative
Rossby waves
d
∂
u
∂
v ∂
∂
=
+
+
+w
dt
∂t
r cos ϕ ∂λ
r ∂ϕ
∂z
In order to simplify, terms of minor importance are
neglected, depending on case of investigation
Continuity equation
Property flux
-J
continuity equation
(U
'A
t-
\y
\d .
Thermal wind
l-
-
/1\
fT
X' X.B
Geostrophic wind
tä +T
\J
r'.i
\J
N F X=
P Ä-t
^"/
A
^q
S
n 'l'
'- r /
i:
u.
5
Primitive equations
0 d y -ü , <
\9
S "..' € ts
ll ä
=+ -
Yi A
tl v). 1 *r
t- )ll/n >
g
Equation of motion
Vorticity
Circulation
Absolute vorticity
Rossby waves
N
,J
0q
tFl
iH
l-.
I F i.
lc n
lc n
Its
IE
l-
IH
l-.
lcn
la
lcn
IO
lf
l\ v
I.<
t ^J
l-
lE
lr-i
lä
laIN
IT
IE H
lI N
IH
IN
Uq l c
Introduction
g
I
I
1-)
t\)
^H
11
üq
7
LU
o
R
a
a
ti
lr
/
>.
Ed
a''
g
lH
tl z
I F-5
l<
Atmospheric
dynamics
t9
X
!Y
f.+
s
-J
I
i-S
a
I i.,
P0q
H
lvl
fa
v:-
(9
H aro
N/ \
(u
To i-
l tG
aia
A
-. H
a \,./
lrr
=m
A.
l-t
N.Kämpfer
0
How is ψ in the volume affected? What is dψ/dt
4
I6
, Ft s
Fr
g;'l ln
H' = Fo )
t_)
-
Fr
H
P
^-\
4
H
E X ! YH
o-i
' -) :
v) x
t_?
tJ.
rt
t+
lr'
(J
|-J
HAqJ
i4
a + = --+
r.'
Äx No:
X
sä^rÄ 2
€
r - . n 5 ;r
ä f+ g --
S
*Qz X
ä 'u
ä'
{)v r
e
IJFH-
N
ri
Fi-
E- ä
X
v:rr A( -
H
V- t
X
H.
*:
tr
' 5 11\
iJ
N
X 'E
F il
+
^J
t9
!
ia
-v J
XUX
Er F
<
/a.i
l-'l
I
V
tP: -S- O
u.
;)
lJ.
-'
1n
u.
F
C' \Y
(U
' v .; n
N
g
aJ
ea
convergenve
(uψ)2 −(uψ)1
<
∆x
>0
g
II
l-)
^H
üq
o
r.
F.
l*.
a
a
I
F
N)
-J
g
(uψ)2 −(uψ)1
∆x
N
O: ( n
Ä
\y
P
i;+
l
A'
A
F
t{ l
'
\v
/n
^
X
14
H
,)
i-{
o
-r n *+tr
eT h F t.J )
H.
,
F-:
:
l-.
F
ALJ r.\ Y l
\
!-\
f-
= .:h x e
t+
A
:1
rr
vH iJ
H.
divergence
l-
q
g
cJ
frA
+
ä|. löe +x
x)
l-/
)-1
r_rO
i,J
;,n
\v
\Y
o o u 5
€-r a
n, F
rPaa-
X o- 9 =
I
Fe
A fluid can transport substances or a property ψ like mass,
density, momentum etc. → Flux of property ψ is ~v ψ
Examples:
I mass flux (per volume): ~
vρ
I heat flux (per mass): ~
v cV T
I momentum flux (per volume): ~
v ρ~v
Consider ψ-flux in a volume:
flux divergence → more ψ flows out than in
flux convergence → more ψ flux flows in than out
Continuity equation
Conservation of mass
Consider densityflux ~v ρ(x, y , z) through a volume dx, dy , dz
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
ρ
Mass-flux in y -direction: v ρ(y + dy ) = v ρ(y ) + ∂v
∂y dy
The flux through area dxdz in the cube is v ρdxdy ρ
The flux out of the cube is accordingly v ρ + ∂v
∂y dy dxdz
∂v ρ
ρ
→ net flux: v ρ + ∂y dy dxdz − v ρdxdy = ∂v
∂y dydxdz
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
In three dimensions → by analogy for the net mass flux:
∂uρ ∂v ρ ∂w ρ
+
+
dxdydz
∂x
∂y
∂z
Continuity equation ctd.
What happens to the mass in case of a divergence, i.e. more
flows out than in?
Mass is conserved → mass will thus decrease in time.
∂m
∂ρV
∂ρ
=
=
dxdydz
∂t
∂t
∂t
⇒ decrease in mass is equal to negative of flux divergence
∂ρ
∂uρ ∂v ρ ∂w ρ
dxdydz = −
+
+
dxdydz
∂t
∂x
∂y
∂z
Divide by volume to obtain continuity equation
∂ρ
∂uρ ∂v ρ ∂w ρ
~ · ~v ρ
=−
+
+
= −∇
∂t
∂x
∂y
∂z
Note
∂ρ
∂t
~ · ~v ρ = −~v · ∇ρ
~ − ρ∇
~ · ~v
= −∇
∂ρ
~ = dρ = −ρ∇
~ · ~v
+ ~v · ∇ρ
∂t
dt
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
Primitive equations
The whole set of equations used to describe atmospheric
dynamics is called primitive equations
d~v
1~
~ × ~v − a~v + ~g
= − ∇p
− 2Ω
dt
ρ
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
the gas law
continuity equation
p = ρRT
Primitive equations
Geostrophic wind
the first law of thermodynamics
Thermal wind
Vorticity
dT
1 dp
Q̇
=
+
dt
cp ρ dt
cp
Circulation
Absolute vorticity
Rossby waves
and the continuity equation
dρ
~ · ~v = 0
+ ρ∇
dt
Geostrophic wind
Consider equation of motion in horizontal direction
d~vh
dt
~ p + F~c + F~R
= F
h
1~
~ vh − a~vh
= − ∇
hp − f k × ~
ρ
Above approx. 1 km friction can be neglected
Air parcel starts to move due to pressure gradient → evokes
Coriolis force → deviation of track to the right → equilibrium
1~
f ~k × ~vh = − ∇
hp
ρ
Vector multiplication with ~k on the left allows to solve for ~vh
⇒ Velocity is called geostrophic wind v~g
v~g =
1 ~ ~
k × ∇h p
ρ·f
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
Geostrophic wind
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
,
Geostrophic wind
v~g =
1 ~ ~
k × ∇h p
ρ·f
vg =
1 ∂p
f ρ ∂x
where
f = 2Ω sin ϕ
ug = −
1 ∂p
f ρ ∂y
Note:
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
I
Geostrophic wind is parallel to isobars
Primitive equations
I
On northern hemisphere → low pressure system on the
left
Geostrophic wind
I
Wind around low pressure system in the same direction
as Earth rotation
I
The denser the isobars the higher the wind speed
I
As geostrophic wind is parallel to isobars (normal to
gradient) → pressure imbalance can not be changed
I
When friction is present → subgeostrophic wind →
pressure imbalance can be changed
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
Geostrophic wind
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
Geopotential height at 500 hPa in decameters and winds
Rossby waves qualitatively
30 mb wave
Geopotential
Example of geopotential
field at 30 mb
Height
Dec. 28, 1997
N.Kämpfer
90
Latitude
Atmospheric
dynamics
60
H
High-Low
Wave 1
pattern
L
30
Introduction
Equation of motion
continuity equation
Primitive equations
0
180
90
0
Longitude
Geostrophic wind
90
Thermal wind
Nov. 18, 1997
Vorticity
Latitude
90
60
Circulation
Absolute vorticity
Rossby waves
H
L
180
90
H
L
Wave 2
pattern
30
0
from electronic textbook about ozone
0
Longitude
90
As we move from east to west, we observe high-low structures.
A single high-low structure is a wave 1 pattern, while 2 high-low
Thermal wind
From geostrophic wind equation together with ideal gas law
1 ∂p
RT ∂p
∂ ln p
fv =
=
= RT
ρ ∂x
p ∂x
∂x
N.Kämpfer
Atmospheric
dynamics
Introduction
From hydrostatic balance
Equation of motion
continuity equation
∂ ln p
g
=
−
RT
∂z
Primitive equations
Geostrophic wind
Cross differentiation and neglecting vertical variations in T
we get
g ∂T
∂v
≈
∂z
fT ∂x
∂u
g ∂T
≈−
∂z
fT ∂y
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
These are the thermal wind equations
They give relations between horizontal temperature
gradients and vertical gradients of the horizontal wind when
both geostrophic and hydrostatic balance apply
Thermal wind
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
oa<
continuity equation
Geostrophic wind
Thermal wind
∂u
g ∂T
≈−
∂z
fT ∂y
\\
trv
l
NJ
\\
tl
(r5
il-r
T decrease in y
I
hr
vv
Primitive equations
from Dutton: Dynamics of atmospheric motion
Latitudinal temperature gradient causes an increase in the
latitudinal pressure gradient
→ geostrophic wind speed increases with height
→ thermal wind is parallel to isotherms
Vorticity
Circulation
Absolute vorticity
Rossby waves
Thermal wind
Example: The zonally averaged zonal wind in the lower and
middle atmosphere of the Earth is close to a thermal wind
January 1979-98 Temperature
48
40
Summer
Winter
20
28
0
-20
0
0
-4
Atmospheric
dynamics
1
260
N.Kämpfer
Introduction
240
40
Equation of motion
240
J
-20
260
continuity equation
220
10
Tropics
0
Polar Vortex
Primitive equations
Pressure (hPa)
0
220
24
20
Height (km)
32
16
100
J
40
Lowestmost stratosphere
220
J
20
-90
Vorticity
Circulation
Absolute vorticity
Rossby waves
220
0
280
-60
0
300
-30
0
260
0
0
Thermal wind
260
20
0
8
240
Lowestmost stratosphere
240
0
200
0
Geostrophic wind
0
Latitude
30
60
1000
90
from electronic textbook about ozone
Clearly visible are jet streams and polar night jet J
Jets are linked with strong gradients in T
Vorticity
In addition to the primitive equations also equations
describing vorticty in a fluid field are of importance
Vorticity, ζ, in a horizontal flow is the vertical component of
the rotation of the velocity field
~ z × ~v = ∂vy − ∂vx = ∂v − ∂u
ζ=∇
∂x
∂y
∂x
∂y
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
I
I
I
Vorticity is a measure of the local (not global) rotation
or spin of the flow at any point in the flow
Vorticity therefore is a field-parameter
Vorticity shows up in two cases:
I
I
in flows that are bending
in straight motion with shear
Geostrophic wind
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
Circulation
In order to determine the direction of rotation in a flow,
circulation is used. Circulation is defined as
I
Z = ~v · d~s
N.Kämpfer
Atmospheric
dynamics
S
Example: Assume border S of area A is a rope “. Tangential
”
components of velocities will act on this rope. If the resulting
tangential velocity is not compensated → rope will rotate.
Introduction
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
I
I
Z > 0 → counter clock wise rotation
Z < 0 → clock wise rotation
Thermal wind
Vorticity
In contrast to vorticity that is defined at each point in a
flow, circulation is valid for an area A and its border s.
Circulation
Absolute vorticity
Rossby waves
A relation between ζ and Z is given by the law of Stokes:
I
ZZ
ZZ
~ n × ~v dA =
Z = ~v · d~s =
∇
ζdA
S
A
Circulation is a measure of the mean vorticity of an area A
Some cases
Simplest case: v = ω · r → Circulation is then
I
Z = ~v · d~s = v · 2πr = 2πr 2 ω
and vorticity by division of the area element
N.Kämpfer
Atmospheric
dynamics
Introduction
Z
ζ = 2 =2·ω
r π
Equation of motion
continuity equation
Primitive equations
In this case vorticity is just two times the angular velocity
Geostrophic wind
Thermal wind
Vorticity
In general
Circulation
Absolute vorticity
Rossby waves
v( r + dr )
=v(r)*$.ot
v(r)
.z\
,'
z\rr2
z/
/.-
-t
.z'--4
l) t'
clg
- -'
ζ=
dZ
v (r ) ∂v
=
+
dA
r
∂r
Vorticity of Jupiter’s red spot
images of the Galileo satellite
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
Choi et al. (Icarus, 188, 35-46, 2007)
Radius of X is about R=70000 km
From image: spot radius ≈ 6 deg → r ≈ 7400 km
Tangential velocity is about v=150 m/s
⇒ ζ = r Z2 π = 2 · ω = 2 vr = ... = 4 · 10−5 s −1
Geostrophic wind
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
Absolute vorticity
So far we have discussed the local vorticity, ζ. In an inertial
reference system we have to add the part stemming from the
planetary rotation, i.e. ω = 2Ω sin ϕ = f
→ The absolute vorticity, η, is thus
N.Kämpfer
Atmospheric
dynamics
Introduction
η =ζ +f
How is η of a two dimensional flow changing with time?
Use general equation of motion in horizontal form
∂~vh
d~vh
~ h )~vh = − 1 ∇
~ h p − f ~k × ~vh
=
+ (~vh · ∇
dt
dt
ρ
Separate in horizontal components
∂u
∂u
∂u
1 ∂p
+u
+v
− fv = −
∂t
∂x
∂y
ρ ∂x
∂v
∂v
∂v
1 ∂p
+u
+v
+ fu = −
∂t
∂x
∂y
ρ ∂y
Build ∂/∂y of first - ∂/∂x of second and rearrange terms
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
Vorticity equation
We obtain the vorticity equation
∂ζ
∂ζ
∂ζ
∂f
+u
+v
+v
=0
∂t
∂x
∂y
∂y
N.Kämpfer
Atmospheric
dynamics
As ∂f /∂t = ∂f /∂x = 0, we can write
Introduction
∂
∂
∂
(ζ + f ) + u (ζ + f ) + v (ζ + f ) = 0
∂t
∂x
∂y
Equation of motion
continuity equation
Primitive equations
Expressed with the absolute vorticity η, we get
∂η
~ h η = dη = 0
+ ~vh ∇
∂t
dt
Geostrophic wind
Thermal wind
Vorticity
Circulation
Absolute vorticity
I
I
η is conserved in a horizontal flow without divergence
For the relative vorticity
Rossby waves
dζ
∂f
= −v
= −v β
dt
∂y
Relative vorticity will change as soon there is a
meridional velocity component
Conservation of total vorticity
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
To leading order, absolute vorticity η = ζ + f is constant:
the relative vorticity ζ simply being exchanged with the
planetary vorticity f
→ Planetary waves set up
Rossby waves
Consider the vorticity equation in two dimensions without
divergence
dη
∂η
~ hη = 0
=
+ ~vh ∇
dt
∂t
that can be expressed as
∂ζ
∂ζ
∂ζ
+u +v
+v β = 0
∂t
∂x
∂y
where
β=
∂f
2Ω cos φ
=
∂y
r
The vorticity equation is a non linear partial differential
equation and analytically not solvable
→ In order to find a solution we linearize (as often in
hydrodynamics):
0
where
u ū
= v̄ + v 0
where
v 0 v̄
ζ = ζ̄ + ζ 0
where
ζ 0 ζ̄
u = ū + u
v
0
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
¯ are mean values and (...)0 are disturbances
(...)
We neglect products of disturbances as they are small
Rossby waves
This will lead to a linearized vorticity equation
∂ζ 0
∂ζ 0
∂ζ 0
∂ ζ̄
0 ∂ ζ̄
+ ū
+u
+ v̄
+ v0
+ v 0β = 0
∂t
∂x
∂x
∂y
∂y
Assume a constant flow in zonal and none in meridional
∂ū
direction → ū = u0 =const., v̄ = 0 → ζ̄ = ∂v̄
∂x − ∂y = 0
This simplifies the linearized vorticity equation
∂ζ 0
∂ζ 0
+ u0
+ v 0β = 0
∂t
∂x
As disturbance is only in v , i.e. u 0 = 0 → ζ 0 = ∂v 0 /∂x.
∂2v 0
+ u0
∂2v 0
∂x 2
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
Thermal wind
Vorticity
Circulation
Absolute vorticity
+ v 0β = 0
∂t∂x
Ansatz: v 0 only depends on x, no variation in y direction
2π
v 0 (x, t) = v0 cos
(x − ct)
L
v0 : constant amplitude, L: wavelength and c: phase speed
Rossby waves
Rossby waves
This leads to
2
4π
4π 2
2π
(x − ct) = 0
c − 2 u0 + β v0 cos
L2
L
L
Expression in [ ] brackets must be zero
We finally obtain the famous Rossby equation
βL2
c = u0 − 2
4π
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
Thermal wind
I
I
I
Phase speed depends on wavelength → dispersion
Stationary wave for c = 0. Wave does not move
r
u0
Lstat = 2π
β
Vorticity
Circulation
Absolute vorticity
Rossby waves
With u0 ≈ 15m/s and β ≈ 6.3 · 10−11 m−1 s−1
Lstat ≈ 6300 km
I
These waves are called long waves or Rossby waves
Rossby waves examples
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
Atmospheric physics - an interdisciplinary science
I
Thermodynamics
I
I
I
hydrostatic equilibrium, lapse rates
water and its transformations
Radiation
I
I
I
Insolation
Absorption, emission, scattering → heating, cooling
Spectroscopy, radiative transfer
I
I
I
Chemistry
I
I
I
I
Chapman layer
Radiative forcing
Thermodynamics of chemical reactions
Chapman model of O3 formation
aerosols, heterogeneous reactions → ozone hole
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
Dynamics
I
I
Temp. differences → pressure differences → fluid motion
Earth is rotating → Coriolis force
I
I
Geostrophic wind, thermal wind
waves (Rossby, gravity), circulation, vorticity, PV
This is the end
N.Kämpfer
Atmospheric
dynamics
Introduction
Equation of motion
continuity equation
Primitive equations
Geostrophic wind
Thermal wind
Vorticity
Circulation
Absolute vorticity
Rossby waves
... if you think physics of planetary atmospheres is interesting
you might like to contact me for a master thesis
→ room A101