* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Tree Structure for Set of Intervals
Survey
Document related concepts
Transcript
Tree Structure for Set of
Intervals
Interval Tree
• Stores a set of intervals
• Find (X) : returns all intervals that contains X
Key Points
• Key of the node is contained in [ai, bi ]
• Interval [ai, bi ] is contained in the interval associated with the node.
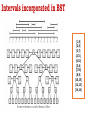
Intervals incorporated in BST
[1,9]
[2,4]
[3,7]
[3,11]
[4,12]
[5,6]
[7,16]
[8,9]
[10,15]
[13,15]
[14,16]
Data Structures
Node
List
Query an interval Tree
Time Complexity
Basic Operations / Functions
Static data structure
• Create once
• Update
Not Possible
• Insert
• Delete
Create
• Get the interval set
• Extract the interval endpoints
• Sort the endpoints
X= { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16}
• Construct BST with the end points and then
incorporate the intervals as discussed in slide 3
[1,9]
[2,4]
[3,7]
[3,11]
[4,12]
[5,6]
[7,16]
[8,9]
[10,15]
[13,15]
[14,16]
Segment Tree
Canonical Decomposition
Example
Root nor any node on the left or right boundary path of the tree can have any intervals of the canonical
interval decomposition attached to it because their node intervals are unbounded and we are
representing only finite intervals.
Trees for union of intervals
“Klee’s Measure Problem.”
He asked whether it is possible to determine the measure (length) of a union of
n intervals in time better than Θ(n log n).
A simple solution
In O(n log n) would be to sort the interval endpoints and then sweep from the
smallest endpoint up, keeping track of the number of intervals that the current
point belongs to.