* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download File - Physics with Miss OO
Survey
Document related concepts
Transcript
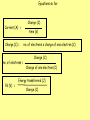
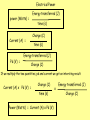
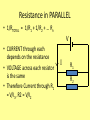
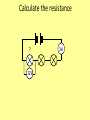
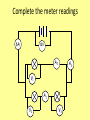
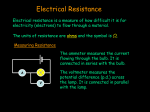
Year 12 Current Electricity Lesson 4a Pd, Power and Resistance Miss O’Donnell Recap on what we have done • Potential difference is the work done (or energy transferred) per unit charge, measured in volts • V= W/Q • Work is done when charge Q flows through a component • W = QV • Electrical power = Energy Transfer / Time • P = VI see derivation on next slide Electrical power & current • A component has a pd V across its terminals and a current I passing through it. • In time ∆t – the charge through the component Q=I ∆t – the work done by the charge carriers W=QV – By substitution W= (I ∆t)V = IV∆t • Because Power = Energy/Time = IV∆t/ ∆t • Power = IV Energy Transfer in Electrical Devices • The emf of a source of electricity is defined as the electrical energy produced per unit charge passing through the source. • Unit is the VOLT – same as pd • For a source of emf ε in a circuit, the electrical energy produced when a charge Q pass through the source is Qε • This energy is transferred to other parts of the circuit and some may be dissipated by the source itself due to internal resistance – we will explore this further later Equations so far Current (A) = Charge (C) = no. of electrons = Pd (V) = Charge (C) time (s) no. of electrons x charge of one electron (C) Charge (C) Charge of one electron (C) Energy transferred (J) Charge (C) Electrical Power The power of this light bulb is 40 watt. It transfers 40 joules of electrical energy into heat and light energy every second. The power of this straightner is 2kW (2000 watt). It transfers 2000 joules of electrical energy into heat energy every second. Power is measured in watts (W). 1 watt of power means that 1 joule of energy is used every second. power (Watts) = energy transferred (Joules) time taken (seconds) Electrical Power Energy transferred (J) power (Watts) = time (s) Charge (C) Current (A) = Pd (V) = time (s) Energy transferred (J) Charge (C) If we multiply the two quantities, pd and current we get an intersting result: Current (A) x Pd (V) = Charge (C) time (s) Power (Watts) = Current (A) x Pd (V) x Energy transferred (J) Charge (C) If we know the power (the rate of energy transferred) by a motor, for example, then it is easy to calculate the amount of energy that is transferred in a particulart time: energy transferred (joules) = power (watts) x time (seconds) Example: A 230V microwave oven has a power rating of 800 W. Calculate: a. the energy transferred in 1 minute b. the current taken by it. Answer: a. Energy trnasferred = power x time 800 x 60 = 48000 joules b. Power = current x voltage current = power / voltage = 800/230 = 3.48 A The power of a torch bulb 3 V; 0.5 A is written on the packet of torch bulbs. 1. Use your ideas about electrons to describe the mechanism of the energy transfer when the torch is 'on'. 2. Calculate the power conversion for the bulb in normal use. 3. The life of the bulb is approximately 10 hours. How much energy will it have dissipated in its lifetime? Answers 1. Electrons going down a potential difference pass energy to vibrations of atoms in the filament. Energy leaves the filament carried by electromagnetic radiation (light and infrared) 2. 1.5 W 3. 54 000 J Measuring the power of different light bulbs The power of electric lights varies widely, from a fraction of a watt for a torch bulb to several thousand watts for aircraft lights In a darkened room, a number of different lamp bulbs, all running at 12V, can be seen to give very different brightnesses. Their power can be measured in the following way: 1. Use an ammeter and a voltmeter to measure the current I through the lamp and the potential difference V across the lamp. The current is the rate of flow of charge in coulomb per second. The potential difference is the energy in joule per coulomb of charge flowing. Thus the power in joule per second is the current multiplied by the potential difference: P = I V 12 V A V Travelling kettle Kasim has to travel abroad as part of his work. Knowing that not all hotels provide a 'Welcome Tray' he buys a travel kettle so he can always make coffee for himself. The kettle is marked: On the package is written: 'Takes less than 4 minutes to boil on 230 V and 7 minutes on 120 V' 1. Explain the meaning of the power rating: 720 W 2. Why would boiling some water in the kettle in New York (power supply: 120 V) take longer than in Belfast (power supply: 230 V). 3. Calculate the current through the element on each setting. 4. After his trip to New York, Kasim forgets to switch over the voltage setting to 230 V. Why might the kettle be damaged by leaving it at the 120 V setting? 5. Suggest a suitable fuse value to use in the plug to protect the kettle from overheating. Answers 1. 720 J of energy is delivered per second to the kettle to heat the water and surroundings. 2. The water will take longer to heat up in New York since the energy is transferred more slowly. 3. 230 V setting you get 3.1 A; 120 V setting you get 2.8 A 4. Almost double the pd across the element will result in double the current, leading to 4 times the power and serious overheating which will damage the insulation. 5. 5 A fuse will stop too high a current flowing. Current (A) = Charge (C) = no. of electrons = Pd (V) = Charge (C) time (s) no. of electrons x charge of one electron (C) Charge (C) Charge of one electron (C) Energy transferred (J) power (Watts) = Equations so far Charge (C) Energy transferred (J) time (s) Power (Watts) = Current (A) x Pd (V) Resistance & Resistivity • Definitions and laws – Definition of Resistance: the resistance of a component is a measure of the difficulty of making current pass through it. – Definition of Resistivity: is a property of a material. It signifies how strongly the material opposes the flow of electric current. • Ohm’s Law: V=IR or R = V/I measured in ohms (Ω) Resistance • Ohm’s Law: V=IR or R = V/I –measured in ohms (Ω) • Resistance in Series: R Total = R1 + R2 + …+ Rn • Resistance in Parallel 1/R Total = 1/R1 + 1/R2 + 1/R3 + .. + 1/Rn • Resistance in Parallel (for 2 resistors) R Total = R1 x R2/ R1 + R2 Resistance • Ohm’s Law states that the pd across a metallic conductor is proportional to the current through it (provided the physical conditions do not change) • Ammeter measures current THROUGH the resistor • Voltmeter measures pd ACROSS the resistor A R V Resistance Resistance is anything in a circuit that restricts the flow of current It can be calculated using Ohm’s Law: Resistance = (Ohms) The unit of Resistance is the Ohm Voltage (V) V Current (A) I x R Resistance in SERIES • RTOTAL = R1 + R2 + … + Rn • TOTAL Resistance is the SUM of all the resistances in the circuit • CURRENT through each resistor is the same • VOLTAGE across each resistor depends on its resistance • Each resistor acts like its’ own little Ohm’s Law Circuit V I R1 R2 Resistance in PARALLEL • 1/RTOTAL = 1/R1 + 1/R2 + … Rn V • CURRENT through each depends on the resistance • VOLTAGE across each resistor is the same • Therefore Current through R1 = V/I1, R2 = V/I2 I R1 R2 Calculate the resistance ? 12V 3A Complete the meter readings 6A 12V A2 A3 V1 A1 V2 V3