* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download High intensity slow wave structures for relativistic particle
Survey
Document related concepts
Transcript
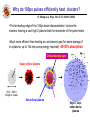
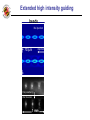
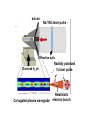
UNIVERSITY OF MARYLAND AT COLLEGE PARK High-intensity optical slow-wave structure for direct laser electron acceleration H.M. Milchberg, B.D. Layer, A. York, J. Palastro, T, Antonsen University of Maryland, College Park HEDSA 2009 Conventional accelerators high energy physics 27 km circumference LEP (CERN) (100 GeV) SLAC (50 GeV) 3 km R > Rmin synchrotron radiation loss constraints: Eaccel<106-7 V/m structure breakdown The SLAC structure is periodically modulated Etransverse Btransverse Ez EM propagation & particle accel. ‘slow-wave’ structure wave phase velocity < c accelerator waveguide structure internal breakdown (lightening!) and self-destruction if wave fields are greater than ~ 107 Volts/m Solution: use ‘milder’ fields over longer distance view from space 50 GeV/(1.7x107 V/m) ~ 2 miles ‘conventional’ laserplasma wakefields: intense laser pulse enters gas jet and relativistic electron beam emerges relativistic electron beam relativistic electron spectrometer 150 m Plasma oscillation: “wake-field” pulse speed is vg < c - + E E + E E + E Laser pond. force for >1018 W/cm2 pushes electrons out of the way (e) (e) 100ps Nd:YAG laser pulse 13 µm 13µm But can we imitate SLAC using a plasma? (a) 200 35 fs Ti:Sapphire laser pulse 200µm (b) r (µm) YES! Axially modulated plasma waveguide Radially modulated Axicon -200 0~35 μm (c) 50 fs transverse interferometer probe 300 µm z (µm) 50µm 35 µm 1000 (d) 50µm 35µm Principle of plasma waveguide: example of hydrodynamic shock generation experimental electron density profiles after pulse: Plasma cross-section during and immediately after pulse: 104 bar pressure blast wave expansion “hollows” the Ne profile 0 25 radius (m) A hollow electron density profile acts as a focusing element plasma index of refraction n2 1 N e (r ) N cr Ne(r) lower in middle results in index n larger there focusing ‘Slow wave’ structure Particle acceleration quasi-phase matching EM wave generation Charged particle dephasing vparticle < vwave phase Phase mismatch vpump ≠ vgenerated electron Ez Epump z-vphaset z-vpumpt vphase>c Lcoherence k Lcoherence= Slow wave picture r z d Bloch-Floquet condition: E (r , z, ) u(r , z, ) exp( ik 0 z ) where u(r , z d , ) u(r , z, ) u (r , z d , ) u~(r , ) am exp( ik m z ) where km 2 m / d m Wave number of mth axial harmonic m k0 2m / d mth harmonic is ‘slow’ if v phase,m / m c Electron acceleration: slow wave picture Electron energy gain U e E v dt e u~ exp i (k0 z t ) ( am exp( ik m z )) v dt m L z U e E v dt e dz u~ am exp i ( dz ' (k0 k m / v)) 0 m For the ‘matched’ case get k0 kn / v 0 U eE0 an L dt dz' / v Quasi-phase matching picture Example: density modulation Mod period d=L1+L2 Accelerating region: low plasma density (high index) Ld1 Ld2 n1 > n2 Decelerating region: high plasma density (low index) The driving wave speeds up and slows down in successive portions of the modulation so that the acceleration in the first part is not completely cancelled by deceleration in the second part. Energy gain per period: U e( Ez1Ld1 Ez 2 Ld 2 ) eE0 ad where a 1 Outline • reminder about clusters -heating and plasma formation with femtosecond pulses (PRLs <2005) -heating and plasma formation with long (many picosecond) pulses • formation of axially modulated (corrugated) plasma fibres using long pulses - axially modulated heating pulse - tailored cluster flow • direct laser acceleration Clusters are essential! Clusters TOF mass spectrum† Signal 60 Electrons/photons 40 X-ray signal* few Å ~ 500 Å ~10-107 atoms— explode in < 1 ps Ions 20 0 0 5 10 Time (s) 15 Energetic electrons/ions Neutrons >90% laser absorption X-rays Laser pulse Cluster jet EUV Scattering EUV spectrum* X-rays: A. McPherson et al., PRL 72, 1810 (1994). EUV and x-rays: * E. Parra et al., PRE 62, R5931 (2000). Optical properties: Kim, Alexeev, Milchberg, PRLs 2003, 2005 Fast electrons and ions: Y. L. Shao et al., PRL 77, 3343 (1996); † V. Kumarappan et al., PRL 87, 085005 (2001). Nuclear fusion: T. Ditmire et al., Nature (London) 398, 489 (1999). Why do 100ps pulses efficiently heat clusters? H. Sheng et al, Phys. Rev. E 72, 036411 (2005) •The far leading edge of the 100ps beam disassembles / ionizes the clusters, leaving a cool high Z plasma that the remainder of the pulse heats. •Much more efficient than heating an unclustered gas (for same average Z in a plasma, up to 10x less pump energy required) -40-50% absorption High Z, cool, under-dense plasma 50 Å ~ 600 Å Single Ar cluster Sub-critical plasma a Super-critical plasma Critical density layer Cryogenic cluster jet •enhanced absorption, even for very long (100ps) pulses • because absorption is local to a cluster, can ultimately form plasma channels with Ne ~ 1018 cm3 electron density* and lower 2 cm • efficiently makes plasma channels in anything that decently clusters • Typically 10X more efficient than for equivalent vol. average pressures of unclustered gas Controlled cryogenic cooling of the jet enhances clustering First modulation method- modulated Bessel beam and uniform cluster flow 100-300mj 100ps Nd:YAG pulse, axially modulated with diffractive optics, incident on unmodulated cluster jet flows Ex. ~2mm corrugation period 1.5 cm 1.5cm Breakdown in atmosphere Breakdown in Argon clusters Guiding in corrugated hydrogen plasma channels 15µm (b) (i) (ii) (iii) 1017 W/cm2 500 µm • H2 jet cryogenically cooled to enhance clustering • Electron densities of ~1.5*1018 cm-3 on axis and ~3*1018 cm-3 at channel wall for a delay of 1ns 700 µm 200 mJ 300 mJ 500 mJ + misalign. Waveguide generation pulse energy and alignment controls modulation features Extended high intensity guiding beads continuous No injection 700µm No injection injection Pump scattering injection Pump scattering Abel inversion Abel inversion 1 mm Extended high intensity guiding 660µm without injection 1018cm-3 8 6 injection, 2x1017 W/cm2 at exit 4 laser 2 3 mm Propagation simulation using the code WAKE* (b) 1018 W/cm2 1.0 Simulation using experimental density profiles Energy flux 0.2 µ 90 m z z 0.9 cm * P. Mora and T. M. Antonsen Jr., Phys. Plasmas 4, 217 (1997). r Attenuation from leakage at gaps Second method: wire-tailored cluster flow, unmodulated laser pulse uniform 500mj 100ps Nd:YAG pulse incident on axially modulated Argon cluster target 1mm corrugation period 1.5 cm Features persist for the full life of the waveguide B.D. Layer et. al, Opt Express 17, 4263 (2009) Nitrogen cluster target @ Argon cluster target @ -150 deg C, 25 m wires 22 deg C, 25 m wires 0.5 ns 0.5 ns 1.0 ns 160 μm 1.0 ns 2.0 ns 2.0 ns 6.0 ns 6.0 ns 600 μm 600 μm (200 consecutive shot averages) 320 μm Direct laser acceleration- inverse Cherenkov acceleration (ICA) 580-MW peak power 31 MeV/m. 10 TW peak powers are now routine, but the need for neutralgas phase matching strongly limits peak intensities. axicon Nd:YAG laser pulse Diffractive optic Clustered H2 jet Corrugated plasma waveguide Radially polarized fs laser pulse Relativistic electron bunch Corrugated guide: simple estimates of dephasing lengths and acceleration gradients Estimate acceleration gradients using index modulation: One full dephasing cycle Accelerating-phase region: low index λ = 800nm } Ne1 = 3*1018 cm-3 Ne2 = 6*1018 cm-3 wch = 12μm p = 1, m = 0 Ld1= ~260 μm Ld2=~165 μm n1 > n2 Decelerating-phase region: high index For P = 1 TW, Ez =0.55 GV/cm, giving an effective gradient of 77 MV/cm Wakefield comparison: Malka et al. used a 30 TW laser at λ = 0.8 μm to produce an acceleration gradient of ~0.66 GV/cm This is a linear process with no threshold. 1 mJ regenerative amplifier alone P = 20GW Effective accel. gradient: 11 MV/cm Direct laser acceleration- energy gain • electrons distributed uniformly on axis 1 to 11 m behind pulse peak • no transverse momentum m=1 phase velocity matched to initial electron velocity Ideal scaling 0 400 o=1000 400 v p,1 v z ,o m=1 phase velocity set to c o=100 v p,1 c o=1000 Ideal scaling o=100 o=30 30 time (ps) 60 o=30 0 30 time (ps) it is better when electrons catch up with a faster wave than to start them phase matched to a slower wave 60 Comparing direct accel to other schemes parameters used for comparison: =800 nm wch=15 m ao=.25 no=7x1018 cm-3 =.9 m=.035 cm o=100 z=300 fs*c for direct accel we have: 2 2 z p 2 2 4a0 1 2 p2 w ch w ch = 1000 vacuum beat wave acceleration: 2 ao wch 1 1 1 2 2f i2 8 2 = 8.3 semi-infinite vacuum acceleration: 1 ao o 2 = 12.5 (best case scenario) (1=22) laser wakefield acceleration: 2 2 2 a p p 1 1/ 2 2 2 (1 a /2) w ch 2 0 2 0 = 14.3 Electron Beam Density final electron density 1 81m num. (a.u.) xf -81m • density peaks off axis; beam has acquired sizeable transverse spread • off-axis peaks mostly composed of low energy electrons 0 number averaged final momentum 300 81m pz (mec) xf -81m -11 m z f -1 m 0 • high energy electrons remain confined to center of beam only the ponderomotive transverse force is significant for these electrons Summary • Can make modulated plasma waveguides with two distinct methodsmodulating either the laser heating profile or the clustered target flow • Can control nearly every aspect of the waveguide by varying cluster parameters and pump laser intensity • Gas cluster channels can be more than 10X less dense than unclustered gas channels (1017’s-1018 ’s vs. 1019 ’s) and use 10X less laser energy for generation- • Cluster-generated plasma waveguides are extremely stable (longitudinal AND transverse) and can support finely engineered structures. • One application: Direct laser accelerator optical-frequency LINAC with no damage threshold