* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Linear Growth Rate in Dynamic Dark Energy Models
Survey
Document related concepts
Transcript
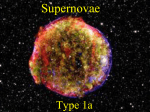
in Dynamic Dark Energy Models 1. Accelerating expansion & interpretation 2. What is Dynamic dark energy model 3. recent observational results Accelerating expansion observations revealed that our universe is not only just expanding, but in a phase of accelerating expansion.(1998) So let’s take a glance at type Ia supernova Type Ia supernova What is it? : Thermonuclear explosion of white dwarf (WD) (identifying from spectra) WD is a remnant of a star and supported by electron degeneracy pressure against gravity, and there is maximum mass limit that can be supported by the pressure. when exceeding the mass limit (through mass accretion or merging from companion star), WD collapses to explode as type Ia supernova -> so, all the type Ia release roughly same energy (luminosity) => we know the luminosity, whenever and wherever it explodes. Type Ia supernova we can exploit this homogeneity of luminosity of type Ia in observation. Assuming constant energy density for the ‘unknown’ (i.e. non time-varying), expansion history follows from the Friedmann eq. : a 2 2 H ( z ) ( ) H 0 ( m , 0 (1 z )3 , 0 ) a 2 Accelerating expansion ..which means - There is unknown component which make the universe accelerate (call it ‘dark energy’) - and it began to domi nate at the present epoch (but why now? ) QCDM proposal ΛCDM - there are ‘dark energy’ term, which is constant with time. ( called ‘cosmological constant’ or denoted as Λ ) Dynamic dark energy model (Quintessence-CDM) - there are ‘dark energy’ term, which varies with time - features are specified by ‘equation of state of dark energy’ - different QCDM model give different , in turn, H(z) Cosmic coincidence Why QCDM models proposed, if constant Λ is the simplest candidate which exerts negative pressure and seems consistent with observations ? -> mostly to address ‘why now?’ problem i.e. why necessarily did it become dominant at the present epoch? Any earlier, would have prevented structures to form in the universe. equation of state - w w defined as (for any energy component) equation of state - w w defined as (for any energy component) for matter : => equation of state - w w defined as (for any energy component) for radiation : => equation of state - w w defined as (for any energy component) for Λ-component : equation of state - w two branches of QCDM - constant w (≠-1) QCDM models - time-varying w(z) QCDM models equation of state - w two branches of QCDM - constant w (≠-1) - w(z) Constant w QCDM - for constant w QCDM models, only w < -1/3 considered, since this range yields acceleration ( 1 wQ 3 ) w(z) QCDM models generally, in w(z) QCDM models, - the dark energy is described as a scalar field slowly rolling down a potential V, - in consequence, w(z) varies with time w(z) QCDM models Rolling scalar field as in the inflation theory extreme slow roll case : if V >> K, w-> -1 to yield negative pressure (w<0), slow roll is needed. (the faster it rolls, the larger K, the larger w) focus on one w(z) model.. “Tracker model” Zlatev, Wang, & Steinhardt (1999) for example, for the potential (where are model parameters) the equation of motion has a solution “Tracker model” ”tracker model” looses ‘why now’ problem : solution extremely insensitive to initial conditions - variations in the initial ratio of the Q-energy(dark energy) density to the matter density by nearly 100 orders of magnitude leads to the same final expansion. i.e. the tracker models are similar to inflation in a sense that they funnel a diverse range of initial conditions into a common final state “Tracker model” for , equation of state given like : , where is the equation-of-state of the background , so when rad-dominated : when matter-dominated : when Q-dominated : matter-dominated : Q-dominated : according to observations, the present epoch is between matter-dominated and Q-dominated, -> thus, is expected. peaks of CMB, d L ( z) , D( z) , ... luminosity distance at z linear growth rate D(z) - affects object formation for the case of for the case of varying w(z), (Basilakos;2003) with dependent of from type Ia + CMB + BAO for constant w QCDM : for w(z) QCDM : - for the special case of (Linder) It is very hard to distinguish observationally Between constant w and w(z) If varies slowly with time (slow-roll) then, observational predictions are well approximated by treating w(a) as a constant with, (Wang et al. 2000) i.e. for w(a) models with diff. potential, always there is effective constant w, which expects nearly same observable quantities in value Summary observation (SN Ia, etc) “dark energy” constant ΛCDM time-varying QCDM constant w w(z) hard to distinguish observationally