Download PP Section 5.1

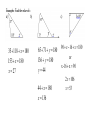
Geometry Section 5.1
Angles of triangles
What you will learn:
1. Classify triangles by sides and angles
2. Find interior and exterior angle measures
of triangles
Recall from section 1.4 that a triangle is a
polygon with 3 sides.
3 congruent angles
3 acute angles
1 right angle
1 obtuse angle
3 congruent sides
2 congruent sides
no congruent sides
right isosceles
acute scalene
AC 
7  0  1  3  7    2 
1  02   1  32  12   42 
BC 
1  7    1  1
AB 
2
2
2
2
2

2
 6   2
2
2
53
17
Scalene
 40
1 3  2
Slope of AB 

70
7
1 3  4
Slope of AC 

1 0
1
1 1  2 1
Slope of BC 


1 7  6 3
Not a right triangle
Theorem 5.1 Triangle Sum Theorem
The sum of the measures of the interior
angles of a triangle is __________.
180
(proof on p.234 of the text)
y
35  118  x  180
153  x  180
x  27
65  71  y  180
136  y  180
y  44
44  x  180
x  136
90  x  16  x  180
or
x - 16  x  90
2 x  106
x  53
The angle of x° in example b) is called an exterior angle
of the triangle. An exterior angle of a triangle is formed
by extending a side of the triangle.
Note that the exterior angle will form a ____________
linear pair
with an interior angle of the triangle.
In example b) we found x to equal _____.
136 Note that
65  71  136
__________________.
This work leads us to the
following theorem.
the sum of the
measures of the two nonadjacent interior angles.
1
2
3
2 x  10  x  65
x  55
A corollary to a theorem is a statement that
can be proved easily using the theorem.
Example c) on the previous page illustrates
the following corollary:
Corollary 5.1 Corollary to the Triangle Sum Theorem
supplementary
The acute angles of a right triangle are ___________
HW: pp 236 – 238 /
3-7, 10-24, 29-36, 38, 49-52