Download Wet-Sprinkler-Rain Example

Used in Spring 2012, Spring 2013, Winter 2014 (partially)
1. Bayesian Networks
2.Conditional Independence
3.Creating Tables
4.Notations for Bayesian Networks
5.Calculating conditional probabilities from
the tables
6.Calculating conditional independence
7.Markov Chain Monte Carlo
8.Markov Models.
9.Markov Models and Probabilistic methods
in vision
Introduction to
Probabilistic Robotics
1. Probabilities
2. Bayes rule
3. Bayes filters
4. Bayes networks
5. Markov Chains
new
next
Bayesian Networks and
Markov Models
• Bayesian networks and Markov models :
1. Applications in User Modeling
2. Applications in Natural Language
Processing
3. Applications in robotic control
4. Applications in robot Vision
many many more
Bayesian Networks (BNs) –
Overview
• Introduction to BNs
– Nodes, structure and probabilities
– Reasoning with BNs
– Understanding BNs
• Extensions of BNs
– Decision Networks
– Dynamic Bayesian Networks (DBNs)
Definition of Bayesian Networks
• A data structure that represents the dependence
between variables
• Gives a concise specification of the joint probability
distribution
• A Bayesian Network is a directed acyclic graph (DAG) in
which the following holds:
1. A set of random variables makes up the nodes in the
network
2. A set of directed links connects pairs of nodes
3. Each node has a probability distribution that quantifies
the effects of its parents
5
Conditional
Independence
The relationship between :
– conditional independence
– and BN structure
is important for understanding how BNs work
6
Conditional Independence – Causal Chains
• Causal chains give rise to conditional independence
A
B
C
P(C | A  B)  P(C | B)
• Example: “Smoking causes cancer, which causes
dyspnoea”
A
smoking
B
cancer
C
dyspnoea
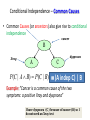
Conditional Independence – Common Causes
• Common Causes (or ancestors) also give rise to conditional
independence
cancer
B
Xray
dyspnoea
A
C
P(C | A  B)  P(C | B) (A(A
indep
C)| C)
B |B
indep
Example: “Cancer is a common cause of the two
symptoms: a positive Xray and dyspnoea”
I have dyspnoea (C ) because of cancer (B) so I
do not need an Xray test
Conditional Dependence – Common Effects
• Common effects (or their descendants) give rise to
conditional dependence
pollution
A
C
smoking
???
B
pollution
cancer
cancer
P( A | C  B)  P( A) P(C )  ((A indep C) | B)
• Example: “Cancer is a common effect of pollution and
smoking”
Given cancer, smoking “explains away” pollution
We know that you smoke and have cancer, we do not need to
assume that your cancer was caused by pollution
Joint Distributions for describing
uncertain worlds
• Researchers found already numerous and dramatic
benefits of Joint Distributions for describing uncertain
worlds
• Students in robotics and Artificial Intelligence have to
understand problems with using Joint Distributions
• You should discover how Bayes Net methodology
allows us to build Joint Distributions in manageable
chunks
10
Bayes Net methodology
Why Bayesian methods matter?
1. Bayesian Methods are one of the most important conceptual
advances in the Machine Learning / AI field to have emerged since
1995.
2. A clean, clear, manageable language and methodology for
expressing what the robot designer is certain and uncertain about
3. Already, many practical applications in medicine, factories,
helpdesks: for instance
1.
2.
3.
P(this problem | these symptoms) // we will use P as probability
anomalousness of this observation
choosing next diagnostic test | these observations
11
12
Problem 1:
Creating Joint
Distribution Table
• Joint Distribution Table is an
important concept
Probabilistic
truth table
•
•
Truth table of all combinations
of Boolean Variables
You can
guess this
table, you
can take
data from
some
statistics,
You can
build this
table
based on
some
partial
tables
• Idea – use decision diagrams to represent
these data.
Use of
independence
while creating the
tables
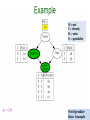
Wet –
Sprinkler –
Rain Example
17
W
S
R
Wet-Sprinkler-Rain
Example
18
Problem 1:
Creating the Joint
Table
Our Goal is to derive this table
Let us observe
that if I know 7
of these, the
eight is
obviously
unique , as their
sum = 1
So I need to guess
or calculate or
find 2n-1 = 7
values
But the same data can be stored
explicitely or implicitely, not
necessarily in the form of a table!!
What extra assumptions
can help to create this
table?
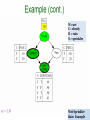
Wet-Sprinkler-Rain
21
Example
Sprinkler on under condition that it rained
Understanding of causation
You need to understand
causation when you
create the table
Wet-Sprinkler-Rain
Example 22
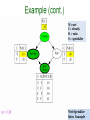
Independence simplifies probabilities
We use independence of variables S and R
P(S|R) = Sprinkler on
under condition that it
rained
S and R are
independent
We can use these
probabilities to create the
table
Wet-Sprinkler-Rain
23
Example
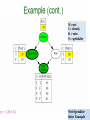
Wet-Sprinkler-Rain
Example
We create the CPT for S and R based on our knowledge of the problem
Sprinkler was on
It rained
Conditional
Probability Table
(CPT)
Grass is wet
What about
children
playing or a dog
pissing?
It is still
possible by this
value 0.1
This first step
shows the
collected data
24
Full joint for only S and R
Independence of S and R is used
0.95
0.90
0.90
0.01
Use chain rule for probabilities
Wet-Sprinkler-Rain
25
Example
Chain Rule for Probabilities
Random variables
0.95
0.90
0.90
0.01
Full joint
probability
• You have a
table
• You want to
calculate
some
probability
P(~W)
Wet-Sprinkler-Rain
Example
Independence of S and R implies calculating fewer numbers to
create the complete Joint Table for W, S and R
Six numbers
We reduced only
from seven to six
numbers
Wet-Sprinkler-Rain
28
Example
Explanation of
Diagrammatic
Notations
such as Bayes Networks
You do not need to build the
complete table!!
You can build a graph of tables or nodes which correspond to certain types of tables
30
Wet-Sprinkler-Rain
Example
Wet-Sprinkler-Rain
Example
Sprinkler was on
It rained
Grass is wet
Conditional
Probability Table
(CPT)
This first step
shows the
collected data
Full joint
probability
• You have a
table
• You want to
calculate
some
probability
P(~W)
When you have this table
you can modify it,
you can also calculate
everything!!
Problem 2:
Calculating conditional
probabilities from the
Joint Distribution
Table
Wet-Sprinkler-Rain
Example
Probability that S=T and W=T
Probability that S=T
= Probability that grass is wet under
assumption that sprinkler was on
Wet-Sprinkler-Rain
36
Example
Wet-Sprinkler-Rain
Example
We will use
this in next
slide
We showed
examples of both
causal inference
and diagnostic
37
inference
“Explaining Away” the facts
from the table
Calculated earlier
from this table
<
Wet-Sprinkler-Rain Example
38
Conclusions on this problem
1. Table can be used for Explaining Away
2. Table can be used to calculate
conditional independence.
3. Table can be used to calculate
conditional probabilities
4. Table can be used to determine
causality
39
Problem 3: What if S and R
are dependent?
Calculating
conditional independence
Conditional Independence of
S and R
Wet-SprinklerRain Example
41
Diagrammatic notation for conditional
Independence of two variables
Wet-Sprinkler-Rain Example
extended 42
Conditional Independence formalized for sets of
variables
S3
S1
S2
Now we will explain conditional independence
CLOUDY - Wet-SprinklerRain Example
Example –
Lung Cancer
Diagnosis
Example – Lung Cancer Diagnosis
1. A patient has been suffering from shortness of breath
(called dyspnoea) and visits the doctor, worried that
he has lung cancer.
2. The doctor knows that other diseases, such as
tuberculosis and bronchitis are possible causes, as
well as lung cancer.
3. She also knows that other relevant information
includes whether or not the patient is a smoker
(increasing the chances of cancer and bronchitis)
and what sort of air pollution he has been exposed to.
4. A positive Xray would indicate either TB or lung
cancer.
46
Nodes and Values in Bayesian Networks
Q: What are the nodes to represent and what
values can they take?
A: Nodes can be discrete or continuous
• Boolean nodes – represent propositions taking binary
values
Example: Cancer node represents proposition “the
patient has cancer”
• Ordered values
Example: Pollution node with values low, medium, high
• Integral values
Example: Age with possible values 1-120
Lung Cancer
47
Lung Cancer Example: Nodes and Values
Node name
Type
Values
Pollution
Binary
{low,high}
Smoker
Boolean
{T,F}
Cancer
Boolean
{T,F}
Dyspnoea
Boolean
{T,F}
Xray
Binary
{pos,neg}
Example of
variables as nodes
in BN
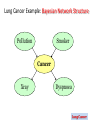
Lung Cancer Example: Bayesian Network Structure
Pollution
Smoker
Cancer
Xray
Dyspnoea
49
Lung Cancer
Conditional Probability
Tables (CPTs)
in Bayesian Networks
Conditional Probability Tables (CPTs) in
Bayesian Networks
After specifying topology, we must
specify
the CPT for each discrete node
1. Each row of CPT contains the
conditional probability of each node
value for each possible combination
of values in its parent nodes
2. Each row of CPT must sum to 1
3. A CPT for a Boolean variable with n
Boolean parents contains 2n+1
probabilities
4. A node with no parents has one row
(its prior probabilities)
51
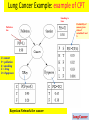
Lung Cancer Example: example of CPT
Smoking is
true
Pollution
low
Probability of
cancer given
state of
variables P and
S
C= cancer
P = pollution
S = smoking
X = Xray
D = Dyspnoea
Bayesian Network for cancer
52
Lung Cancer
• Several small CPTs are used to create larger
JDTs.
The Markov Property for Bayesian Networks
• Modelling with BNs requires assuming the
Markov Property:
– There are no direct dependencies in the system
being modelled which are not already explicitly
shown via arcs
• Example: smoking can influence dyspnoea
only through causing cancer
Markov’s Idea: all information
is modelled by arcs
Software NETICA
for
Bayesian Networks
and
joint probabilities
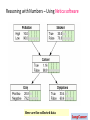
Reasoning with Numbers – Using Netica software
Here are the collected data
56
Lung Cancer
Representing the Joint Probability
Distribution: Example
Pr( P  low  S  F  C  T  X  pos  D  T ) 
We want to calculate this
Pr( P  low) 
Pr( S  F ) 
Pr( C  T | P  low, S  F ) 
Pr( X  pos | C  T ) 
Pr( D  T | C  T )
This graph shows how we can
calculate the joint probability from
other probabilities in the network
P = pollution
S = smoking
X = Xray
D = Dyspnoea
57
Lung Cancer
Problem 4:
Determining Causality
and Bayes Nets:
Advertisement
example
Causality and Bayes Nets:
Advertisement example
• Bayes nets allow one to learn about causal
relationships
• One more Example:
– Marketing analysts want to know whether to increase,
decrease or leave unchanged the exposure of some
advertisement in order to maximize profit from the sale of
some product
– Advertised (A) and Buy (B) will be variables for someone
having seen the advertisement or purchased the product
Advertised-Buy Example
Causality Example
1. So we want to know the probability that B=true given that
we force A=true, or A=false
2. We could do this by finding two similar populations and
observing B based on A=true for one and A=false for the
other
3. But this may be difficult or expensive to find such
populations
–Advertised (A) seen the advertisement
–Buy (B) will be variables for
someone purchased the
product
Advertised-Buy Example
How causality can be
represented in a
graph?
Markov condition and Causal
Markov Condition
• But how do we learn whether or not A causes B at all?
• The Markov Condition states:
– Any node in a Bayes net is conditionally independent of its
non-descendants given its parents
• The CAUSAL Markov Condition (CMC) states:
– Any phenomenon in a causal net is independent of its noneffects given its direct causes
Advertised (A) and Buy (B)
Advertised-Buy Example
Acyclic Causal Graph versus Bayes Net
• Thus, if we have a directed acyclic causal
graph C for variables in X, then, by the Causal
Markov Condition, C is also a Bayes net for the
joint probability distribution of X
• The reverse is not necessarily true—a network
may satisfy the Markov condition without
depicting causality
Advertised-Buy Example
Causality Example: when we learn that
p(b|a) and p(b|a’) are not equal
• Given the Causal Markov Condition CMC, we can infer causal
relationships from conditional (in)dependence relationships
learned from the data
• Suppose we learn with high Bayesian probability that p(b|a)
and p(b|a’) are not equal
• Given the CMC, there are four simple causal explanations for this:
(more complex ones too)
Causality Example: four causal explanations
A causes B
If they advertise more you
buy more
B causes A
If you buy more, they have
more money to advertise
Causality Example: four causal explanations
selection bias
1. Hidden common
cause of A and B
(e.g. income)
In rich country
they advertise
more and they buy
more
A and B are causes for data selection
1.
2.
(a.k.a. selection bias,
perhaps if database didn’t record
false instances of A and B)
If you increase information about
Ad in database, then you increase
also information about Buy in the
database
Causality Example continued
• But we still don’t know if A
causes B
• Suppose
– We learn about the Income (I)
and geographic Location (L) of
the purchaser
– And we learn with high
Bayesian probability the
network on the right
Advertised (A=Ad) and Buy (B)
Advertised-Buy Example
Causality Example - using CMC
• Given the Causal Markov
Condition CMC, the ONLY causal
explanation for the conditional
(in)dependence relationships
encoded in the Bayes net is that
Ad is a cause for Buy
• That is, none of the other
relationships or combinations
thereof produce the probabilistic
relationships encoded here
Advertised (Ad) and Buy (B)
Advertised-Buy Example
Causality in Bayes Networks
• Thus, Bayes Nets allow inference of causal
relationships by the Causal Markov Condition
(CMC)
Problem 5:
Determine
D-separation in
Bayesian Networks
D-separation in Bayesian Networks
• We will formulate a Graphical Criterion of
conditional independence
• We can determine whether a set of nodes X
is independent of another set Y, given a set of
evidence nodes E, via the Markov property:
– If every undirected path from a node in X to a
node in Y is d-separated by E, then X and Y are
conditionally independent given E
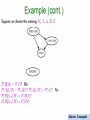
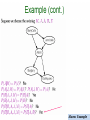
Determining D-separation (cont)
•
A set of nodes E d-separates two sets of nodes X and Y, if every undirected path from a
node in X to a node in Y is blocked given E
•
A path is blocked given a set of nodes E, if there is a node Z on the path for which one of
three conditions holds:
1. Z is in E and Z has one arrow on the path leading in and one arrow out (chain)
2.
3.
Z is in E and Z has both path arrows leading out (common cause)
Neither Z nor any descendant of Z is in E, and both path arrows lead into Z (common effect)
Chain
Common
cause
Common
effect
Another Example of
Bayesian Networks: Alarm
Alarm Example
• Let us draw BN from these data
Bayes Net
Corresponding to AlarmBurglar problem
Alarm Example
74
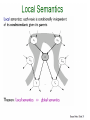
Compactness, Global Semantics, Local
Semantics and Markov Blanket
• Compactness of Bayes Net
Burglar Earthquake
John calls
Mary calls
75
Alarm Example
Global Semantics,
Local Semantics and
Markov Blanket
for BNs
• Useful concepts
76
Alarm Example
78
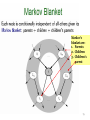
Markov’s
blanket are:
1. Parents
2. Children
3. Children’s
parent
79
Problem 6
How to
systematically Build a
Bayes Network
-Example
81
Alarm Example
83
Alarm Example
84
Alarm Example
So we add
arrow
85
Alarm Example
86
Alarm Example
87
Alarm Example
Bayes Net for the car that does not
want to start
Such networks can be used
for robot diagnostics or
diagnostic of a human done
by robot
88
Inference in Bayes Nets and how to
simplify it
Alarm Example
89
First method of simplification:
Enumeration
90
Alarm Example
91
Alarm Example
Second method: Variable
Elimination
Alarm Example
Variable A was
eliminated 92
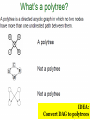
3SAT Example
Polytrees are
93
better
IDEA:
94
Convert DAG to polytrees
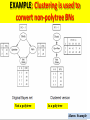
Clustering is used to convert nonpolytree BNs
95
EXAMPLE: Clustering is used to
convert non-polytree BNs
Not a polytree
Is a polytree
96
Alarm Example
• Approximate Inference
1.
2.
3.
4.
Direct sampling methods
Rejection sampling
Likelihood weighting
Markov chain Monte Carlo
97
1. Direct
Sampling
Methods
98
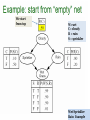
Direct Sampling
Direct Sampling generates minterms
with their probabilities
We start
from top
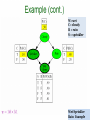
W=wet
C= cloudy
R = rain
S = sprinkler
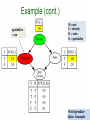
Wet Sprinkler
100
Rain Example
Cloudy =
yes
W=wet
C= cloudy
R = rain
S = sprinkler
Wet Sprinkler
101
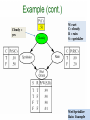
Rain Example
Cloudy =
yes
W=wet
C= cloudy
R = rain
S = sprinkler
Wet Sprinkler
102
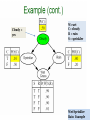
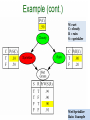
Rain Example
sprinkler
= no
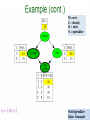
W=wet
C= cloudy
R = rain
S = sprinkler
Wet Sprinkler
103
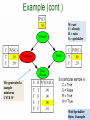
Rain Example
W=wet
C= cloudy
R = rain
S = sprinkler
Wet Sprinkler
104
Rain Example
W=wet
C= cloudy
R = rain
S = sprinkler
Wet Sprinkler
105
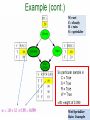
Rain Example
W=wet
C= cloudy
R = rain
S = sprinkler
We generated a
sample
minterm
C S’ R W
Wet Sprinkler
106
Rain Example
2. Rejection
Sampling
Methods
107
Rejection Sampling
• Reject inconsistent samples
Wet Sprinkler
108
Rain Example
3. Likelihood
weighting
methods
109
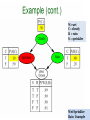
110
W=wet
C= cloudy
R = rain
S = sprinkler
Wet Sprinkler
111
Rain Example
W=wet
C= cloudy
R = rain
S = sprinkler
Wet Sprinkler
112
Rain Example
W=wet
C= cloudy
R = rain
S = sprinkler
Wet Sprinkler
113
Rain Example
W=wet
C= cloudy
R = rain
S = sprinkler
Wet Sprinkler
114
Rain Example
W=wet
C= cloudy
R = rain
S = sprinkler
Wet Sprinkler
115
Rain Example
W=wet
C= cloudy
R = rain
S = sprinkler
Wet Sprinkler
116
Rain Example
W=wet
C= cloudy
R = rain
S = sprinkler
Wet Sprinkler
117
Rain Example
Likelihood weighting vs. rejection
sampling
1. Both generate consistent estimates of the joint
distribution conditioned on the values of the evidence
variables
2. Likelihood weighting converges faster to the correct
probabilities
3. But even likelihood weighting degrades with many
evidence variables because a few samples will have
nearly all the total weight
119
Sources
Prof. David Page
Matthew G. Lee
Nuria Oliver,
Barbara Rosario
Alex Pentland
Ehrlich Av
Ronald J. Williams
Andrew Moore tutorial with the same title
Russell &Norvig’s AIMA site
Alpaydin’s Introduction to Machine Learning site.